Потоки с последействием (потоки Эрланга)

Привет, сегодня поговорим про потоки с последействием потоки эрланга , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое потоки с последействием потоки эрланга , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.

Как мы ранее отметили, интенсивность потока в некотором смысле является математическим ожиданием количества событий в единицу времени (обратная к ней величина указывает на среднее время между событиями). Второй величиной, характеризующей насколько велик разброс во времени прихода событий относительно математического ожидания, является дисперсия.

Допустим, события в потоке следуют точно одно за другим каждые 12 минут без отклонений. Интенсивность такого потока будет равна 5 событий в час. Но если события будут идти случайно, например, 12 ± 2 минуты, то и они в среднем дадут также 5 событий в час. Например, за 200 часов произойдет 1000 событий, величина интенсивности 1000/200 = 5 событий в час. Поэтому по данной характеристике потоки нельзя отличить друг от друга. Но очевидно, что второй поток все-таки будет более случайным, чем первый. Тем более, если в потоке события будут следовать друг за другом 12 ± 10 минут.

Первый поток мы назовем детерминированным, регулярным, второй и третий — случайными. Причем мера случайности с увеличением дисперсии (разброса величины интервала между событиями) будет возрастать. В первом потоке дисперсия равна нулю. Данный факт проиллюстрирован нарис. 29.1.

Рис. 29.1. Иллюстрация регулярного и случайного потоков

Собственно именно дисперсия определяет случайность появления события, слабую предсказуемость момента его появления. Важно уметь управлять этой величиной при моделировании случайных потоков. Если предсказать каждое следующее событие трудно, то поток — без последействия (или с малым последействием, связь между событиями отсутствует, события случайны), если поток детерминирован, то последействие велико — каждой событие практически предсказывает момент появления следующего.

Поток Эрланга k-го порядка — это поток случайных событий, получающийся, если в простейшем (см. лекцию 28) случайном потоке сохранить каждое k-е событие, а остальные отбросить (см.рис. 29.2). Об этом говорит сайт https://intellect.icu . Порядок потока — мера последействия потока. То есть обратной величиной к мере случайности потока является его порядок.

Рис. 29.2. Иллюстрация метода получения потоков Эрланга

Просеивание событий начинает приводить к тому, что между точками появляется последействие, детерминация, которая тем выше, чем больше k. С увеличением k точки ложатся на ось времени все более равномерно, разброс их уменьшается, регулярность увеличивается.

Основано это на том простом и ранее изученном нами факте, что сумма случайных величин есть величина неслучайная (центральная предельная теорема — см. лекцию 25). Чем больше мы сложим случайных величин, тем предсказуемее будет результат (их сумма).

Очевидно, что

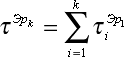
— интервал между событиями в потоке Эрланга k-го порядка.

Плотность вероятности распределения интервалов между случайными событиями в потоке Эрланга k-го порядка:

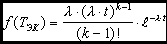
λ_k = λ/k — интенсивность потока Эрланга k-го порядка, где λ — интенсивность простейшего потока Пуассона, а λ_k интенсивность просеянного k раз потока, то есть в k раз меньше.

Параметры закона Эрланга вычисляются по формулам: M_k = 1/λ_k, σ_k = 1/sqrt(k)/λ_k,

Обратите внимание, что в потоке Эрланга M ≠ σ, то есть в потоках с последействием равенство Mи σ невозможно.

Более того, при k –> ∞ событие происходит строго в размеренное время, так как σ –> 0.

Сравните: 
Поток Эрланга 1-го порядка: m = σ₁ — поток без последействия; 
Поток Эрланга i-го порядка: m ≠ σ₂, при этом (σ₂ > 0) и (σ₁ > σ₂) разброс уменьшается, последействие увеличивается; 
Поток Эрланга ∞-го порядка: m ≠ σ = 0 — регулярный поток.

Из этого следует, что порядок потока Эрланга — есть мера последействия потока.

Пример. Рассмотрим пример выхода из строя лампочек на опоре уличного освещения. Примем время наблюдения 100 лет. Из паспортных данных на эти изделия известно, что среднее время работы изделия на отказ составляет 1.5 года; среднеквадратическое отклонение — 0.5 года.

То есть, задано: M_k = 1.5, σ_k = 0.5.

Поскольку M_k ≠ σ_k, то k ≠ 1, то есть мы имеем дело с потоком с последействием. Интенсивность этого потока λ_k = 1/M_k = 1/1.5 = 0.67. Вычисленная интенсивность потока говорит нам о том, что в течение года в среднем перегорает 0.67 лампочки или 67 лампочек за 100 лет.

Так как σ_k = 1/sqrt(k)/λ_k, и равна 0.5, то вычислим порядок потока Эрланга: k = 1/σ²/λ_k² = 1/0.5²/0.67² ≈ 9.

Вычислим интенсивность порождающего потока Пуассона λ = λ_k · k = 0.67 · 9 = 6.

На рис. 29.3 представлен пример алгоритма, реализующего моделирование описанного процесса. Обратите внимание, что берется каждое девятое событие, это обеспечивает достаточно высокую детерминированность потока (то есть малую дисперсию σ_k = 0.5).

Рис. 29.3. Блок-схема алгоритма моделирования появления случайных событий в виде потока Эрланга

Надеюсь, эта статья об увлекательном мире потоки с последействием потоки эрланга , была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое потоки с последействием потоки эрланга и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем

Из статьи мы узнали кратко, но содержательно про потоки с последействием потоки эрланга