Математическое моделирование электрических цепей,Пример моделирования

Привет, Вы узнаете о том , что такое моделирование электрических цепей, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое моделирование электрических цепей , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.

Основные понятия

Структура электрической цепи. Электрическая цепь состоит из приборов, их контакты соединяются друг с другом в точках, которые называются узлами. Мы будем рассматривать приборы с двумя контактами. От узла к узлу через прибор течет электрический ток. Состояние электрического тока в любой момент времени характеризуется его силой (величиной), состояние узла характеризуется потенциалом.

Сила тока. Сила постоянного тока равна заряду, проходящему через поперечное сечение прибора за единицу времени. В общем случае сила тока и заряд связаны интегральным соотношением:

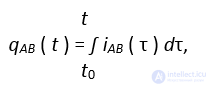
где q_AB ( t ) - заряд, который прошел через прибор от узла A к узлу B с момента времени t₀, когда включили ток, до момента времени t, i_AB ( τ ) - сила ток протекающего через прибор в момент времени τ. Если функция i_AB ( τ ) непрерывна, то i_AB ( t ) = q'_AB ( t ).

Первое правило Кирхгофа. Первое правило Кирхгофа является следствием закона сохранения заряда: сумма сил токов, втекающих в узел, равна сумме сил токов, вытекающих из узла.

Потенциал узла. Потенциал узла равен работе, которую надо затратить, чтобы, преодолевая электростатические силы, перенести единичный положительный заряд из фиксированной точки в данный узел. В качестве фиксированной точки в электротехнике выбирают точку на поверхности Земли, таким образом, потенциал земной поверхности равен нулю. Из закона сохранения энергии следует, что единичный положительный заряд, перемещающийся по электрической цепи из узла A в узел B, приобретает энергию, равную равную разности их потенциалов φ_A - φ_B.

Обобщенный закон Ома. Обобщенный закон Ома утверждает, что величина изменения энергии единичного положительного заряда, проходящего через прибор, пропорциональна силе тока:

падение напряжения на приборе, соединяющем узлы A и B вычисляется по формуле:

U_AB = i_AB R = φ_A - φ_B + e_AB

где i_AB – ток текущий через прибор от узла A к узлу B ( i_AB = - i_BA), R – сопротивление прибора, φ_A – потенциал узла A, φ_B - потенциал узла B, e_AB – электродвижущая сила прибора, e_AB = - e_BA . Если прибор содержит источник электродвижущей силы, то величина этого источника считается положительной в том случае, когда ток проходит через прибор от узла с меньшим потенциалом к узлу с большим потенциалом.

Электрическая цепь, состоящая из источника постоянной электродвижущей силы и сопротивления. Рассмотрим электрическую цепь, состоящую из источника постоянной электродвижущей силы (ЭДС) и сопротивления, положительный полюс источника ЭДС соединяется с контактом сопротивления в узле A, отрицательный полюс источника ЭДС соединяется с другим контактом сопротивления в узле B. Из первого правила Кирхгофа вытекает, что в каждый момент времени сила тока, проходящего от узла A к узлу B через сопротивление, равна силе тока, проходящего от узла B к узлу A через источник ЭДС. Обозначим эту силу тока символом i. Применяя обобщенный закон Ома к источнику ЭДС, получим:

i_AB ∙ 0 = φ_B - φ_A + e_BA

(источник ЭДС является идеальным — его сопротивление равно нулю),

e_BA = φ_A - φ_B.

С другой стороны,

i R = φ_A — φ_B,

где R — величина сопротивления. Таким образом,

i = e_BA / R

Второе правило Кирхгофа. Напишем обобщенный закон Ома для каждого прибора, входящего в замкнутый контур электрической цепи и сложим полученные равенства. Сумма потенциалов всех узлов контура обратится в ноль, так что сумма падений напряжений вдоль замкнутого контура будет равна сумме электродвижущих сил приборов, образующих этот контур (второе правило Кирхгофа).

Электродвижущая сила катушки. Электродвижущая сила катушки (без сердечника) вычисляется по формуле

e_AB ( t ) = - L ( i_AB ( t ))',

где L – коэффициент самоиндукции катушки.

Электрическая цепь, состоящая из источника постоянной электродвижущей силы, катушки и сопротивления. Электрическая цепь состоит из ключа, источника постоянной электродвижущей силы величины e₀, сопротивления и катушки без сердечника; величина сопротивления равна R, коэффициент самоиндукции катушки равен L (надо различать случаи, когда буква L обозначает коэффициент самоиндукции катушки и когда она обозначает преобразование Лапласа). Мы рассматриваем идеальную электрическую цепь - источник электродвижущей силы и катушка не обладают внутренним сопротивлением. В начальный момент времени t = 0 включают электрический ток. Из первого правила Кирхгофа вытекает, что силы токов, протекающих через приборы, образующие электрическую цепь, одинаковы, обозначим силу каждого из этих токов в момент времени t через i ( t ) Применяя второе правило Кирхгофа, получим уравнение

R i ( t ) = χ ( t ) e₀ - L i' ( t ).

В начальный момент времени t = 0 тока в цепи нет: i ( 0 + 0 ) = 0 — это начальное условие нашей задачи.

Электродвижущая сила конденсатора. Заряд, накопленный конденсатором, пропорционален его электродвижущей силе:

q_AB ( t ) = - C e_AB ( t ),

коэффициент C называется электрической емкостью конденсатора.

Электрическая цепь, состоящая из источника постоянной электродвижущей силы, конденсатора и сопротивления. Электрическая цепь состоит из ключа, источника постоянной электродвижущей силы величины e₀, сопротивления и конденсатора; R – величина сопротивления, C — емкость конденсатора. В начальный момент времени t = 0 включают электрический ток. Из первого правила Кирхгофа вытекает, что силы токов, протекающих через приборы, образующие электрическую цепь, одинаковы, обозначим силу каждого из этих токов в момент времени t через i ( t ) Применяя второе правило Кирхгофа, получим уравнение

R i ( t ) = χ ( t ) e₀ - q ( t ) / C.

В начальный момент времени t = 0 заряд конденсатора равен нулю: q ( 0 + 0 ) = 0 — это начальное условие нашей задачи.

Будем считать, что состояние системы описывается значением заряда конденсатора q ( t ), а сила тока является непрерывной функцией времени. Так как

то сила тока представляет собой производную заряда: q' ( t ) = i ( t ),

R q' ( t ) + q ( t ) / C = χ ( t ) e₀.

Формирование математических моделей электрических схем.

Одним из наиболее распространенных методов формирования и реализации математических моделей электрических цепей является метод переменных состояния. Его применение предполагает разделение всех относящихся к схеме электрической цепи переменных на три множества:

• множество входных переменных U={U₁,U₂,…,U_p};
• множество выходных переменных Y={y₁,y₂,…,y_k};
• множество переменных состояния X={x₁,x₂,…,x_n};

В качестве входных переменных рассматривают задающие напряжения e(t) идеальных источников напряжения и задающие токи j(t) идеальных источников тока ,в качестве переменных состояния -токи в индуктивностях i_L(t) и напряжения на емкостях U_C(t), в качестве выходных -все остальные токи и напряжения, которые необходимо определить при расчете.

Математическая модель электрической цепи в методе переменных состояния формируется в виде системы дифференциальных уравнений первого порядка, записанных в нормальной форме (форме Коши):

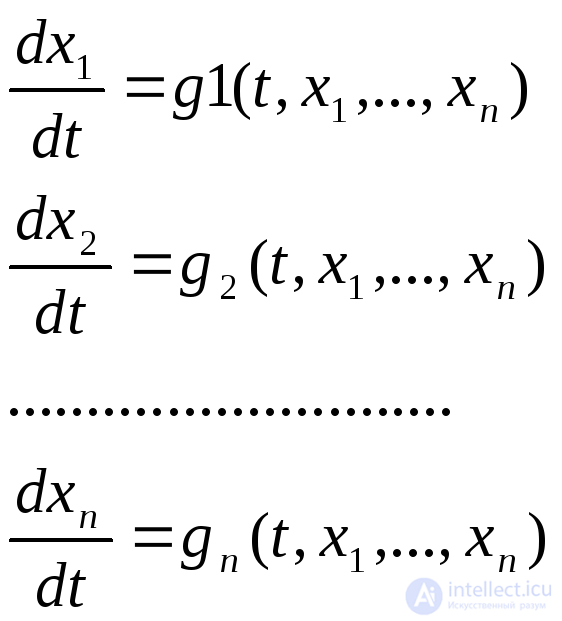(2.7)

Систему дифференциальных уравнений (2.7)удобно представлять в матричном виде:

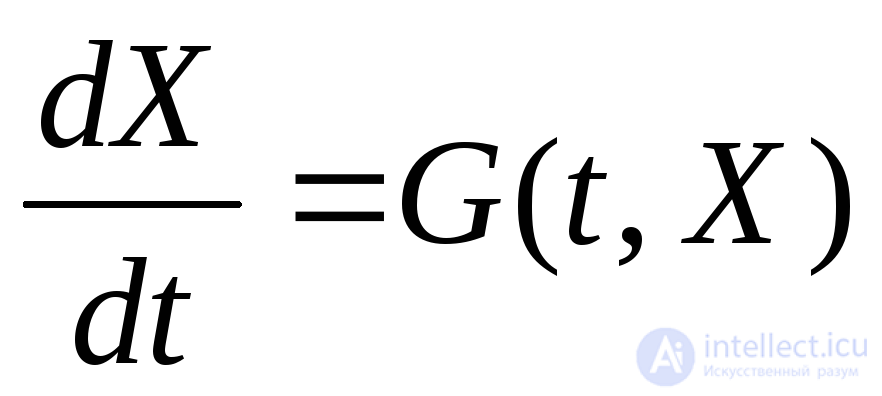(2.8)

где X= [x₁,x₂,…,x_n]^T– одностолбцовая матрица (вектор) переменных состояния;G(t,X) = [g₁(t,X),g₂(t,X),…,g_n(t,X)]^T–n-мерная вектор-функция.

При необходимости определения выходных переменных система дифференциальных уравнений дополняется системой алгебраических уравнений, связывающих выходные переменные с входными и с переменными состояния:

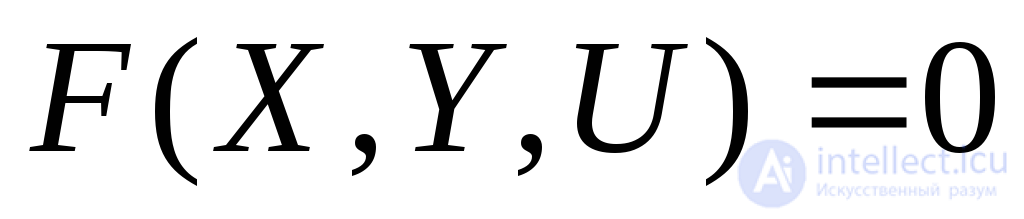(2.9)

где Y= [y₁,y₂,…,y_k]^T- вектор выходных переменных;

F(X,Y,U) = [f₁(X,Y,U),f₂(X,Y,U),…,f_k(X,Y,U)]^T–k-мерная вектор-функция.

Для линейной электрической цепи с постоянными параметрами математическая модель представляет собой систему линейных неоднородных дифференциальных, а также линейных алгебраических уравнений с постоянными коэффициентами:

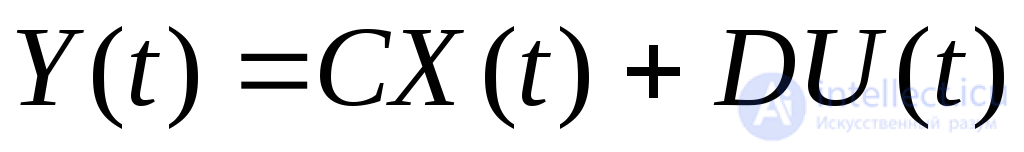(2.10)

где A,B,C,D -матрицы постоянных коэффициентов уравнений, причемА -квадратная матрицаn-roпорядка(n -количество переменных состояния),В-матрица размеромn х р{р -количество входных переменных),С –матрица размеромkхn (k -количество выходных переменных),D -матрица размеромkxp.

Основой формирования математических моделей электрических цепей, содержащих двухполюсные элементы с постоянными параметрами, являются первый и второй законы Кирхгофа и компонентные соотношения (2.1, 2.2) для резистивных, индуктивных и емкостных элементов.

При этом на первом этапе составляется система уравнений:

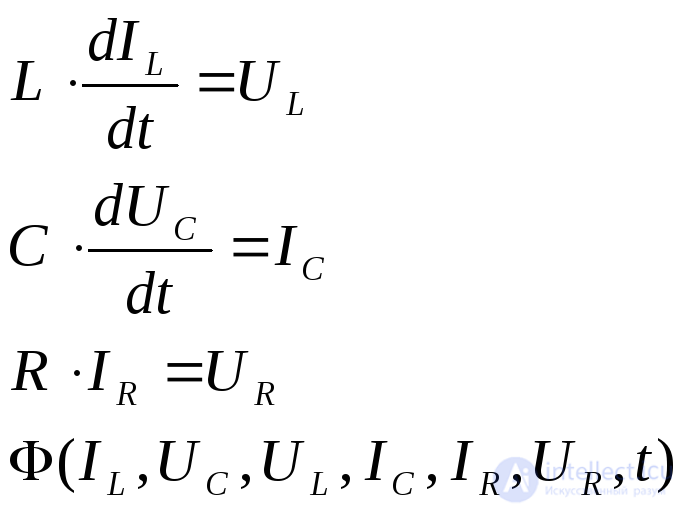(2.11)

Здесь I_L,I_R,I_C– одностолбцовые матрицы токов индуктивностей, сопротивлений и емкостей соответсвенно;U_L,U_R,U_C– одностолбцовые матрицы падений напряжения на индуктивностях, сопротивлениях, емкостях;L,С,R -диагональные матрицы индуктивностей, емкостей, сопротивлений;Ф -одностолбцовая матрица, элементы котрой являются функциями указанных переменных. Об этом говорит сайт https://intellect.icu . Первые два матричных уравнения представляют собой систему дифференциальных уравнений относительно переменных состояния, а два последних -систему алгебраических уравнений, связывающих переменные состояния с остальными переменными.

На втором этапе формирования математической модели систему уравнений (2.11)преобразовывают к системе только дифференциальных уравнений относительно переменных состояния и входных переменных. Для этого из системы алгебраических уравнений выражают переменные U_Lи I_Cчерез переменные состояния и входные переменные и подставляют их в правые части дифференциальных уравнений из (2.11).Однако при этом возможны осложнения, вызванные неполнотой системы алгебраических уравнений. Если система алгебраических уравнений в (2.11)полная, то есть количество переменныхU_L,I_C,I_R,U_Rравно количеству уравнений и система разрешима относительно указанных переменных, то преобразование модели к системе только дифференциальных уравнений возможно, а порядок системы дифференциальных уравнений будет равен числу реактивных элементов в схеме. Если же система алгебраических уравнений неполная, то преобразование к системе только дифференциальных уравнений возможно, однако порядок системы дифференциальных уравнений будет меньше числа реактивных элементов цепи. Такие цепи носят название топологически вырожденных. К топологически вырожденным электрическим цепям относятся цепи, содержащие контуры, состоящие из емкостей и идеальных источников напряжения, а также цепи, содержащие звезды, состоящие из индуктивностей и идеальных источников тока.

Пример моделирования электрической схемы

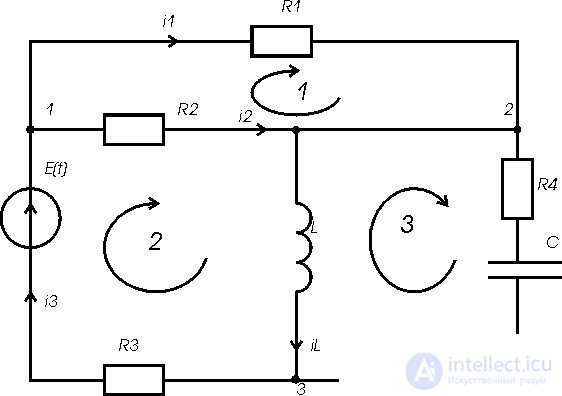
Схемы электрической цепи рис 3.1

1. Задающее напряжение
2. Значение не варьируемых параметров E_o=110B; E_C=50B; E_S=50B; R₁=1 Ом; R₂=1ОМ; R₃=1 Ом; R₄=100 Ом; R₅=100 Ом; T=0,01c;
3. диапазон варьируемых параметров
4. Выходная переменная: Ur3
5. Метод интегрирования: Трапеций
6. Метод оптимизации: Координатного спуска;
7. Определение коэффициента пульсаций: Непосредственный.

Решение

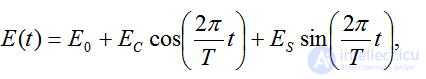
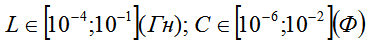
количество узлов Nузл = 3

количество ветвей Nв =5

количество ветвей содержащих только идеальную ЭДС = 0

количество ветвей содержащих только идеальный источник тока = 0

В соответствии с ( ) по первому закону Кирхгофа необходимо составить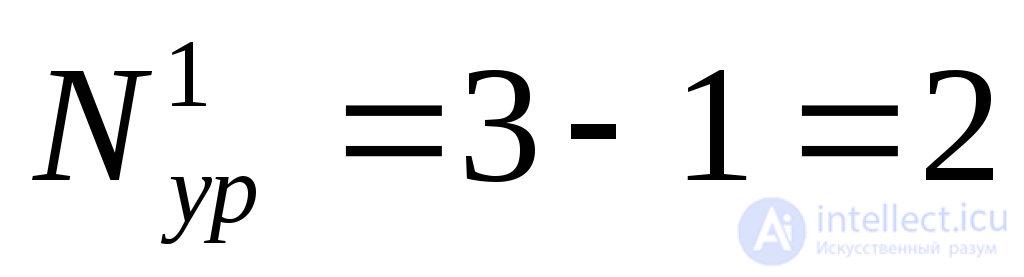

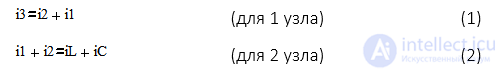
необходимое число уравнений по второму закону Кирхгофа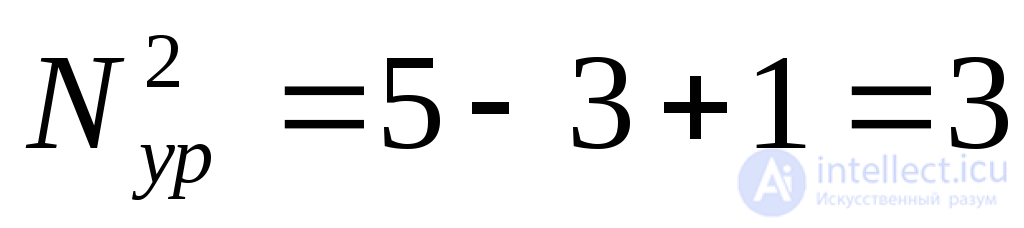

Компоненты соотношения для схемы:

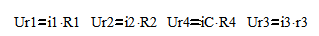
В уравнение (5) подставим Ur4 получим:

Из уравнения (2) выразим iCи подставим в уравнение (6):

Выразим ток i3 из уравнения (4):

Приравняем уравнения (8) и (1)

Заменим Ur2, получим:

Из уравнения (3) выразим i1:

Уравнение (11) подставляем в уравнение (10):

Из уравнения (12) находим i2

В уравнение (7) подставляем уравнение (11)

Уравнение (14) подставляем в уравнение (13):

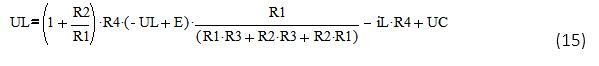
Выражаем UL:

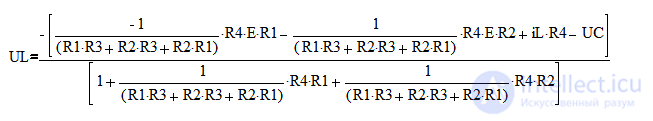
Упростим, получим:

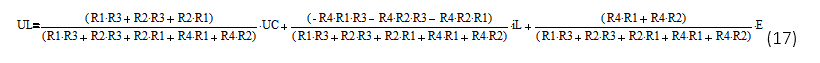
Учитывая соотношение: 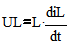получим:

Тогда:

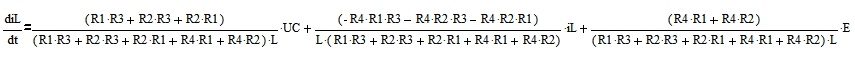
Из уравнения (5)

Подставим уравнение (17) в уравнение (18)

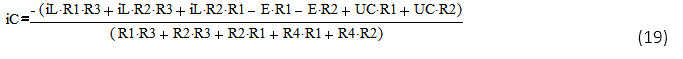
Сгруппируем данные:

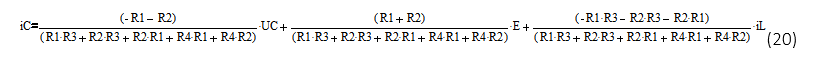
Учитывая соотношение 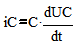получим:

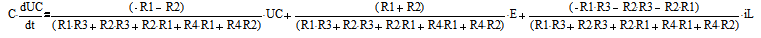
Тогда

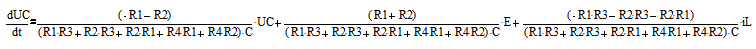
Выразим заданную выходную переменную Ur3 из уравнения (4)

Учитывая соотношение 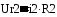, получим:

Подставляя i2 из уравнения (13)

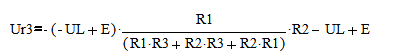
Подставляем UL

Математическая модель представляет собой систему двух дифференциальных уравнений первого порядка с постоянными коэффициентами:

Представим систему уравнений в матричной форме:

,

или, учитывая характер задающего напряжения:

,

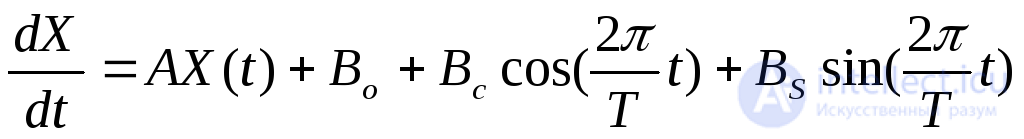где - вектор переменных состояния;

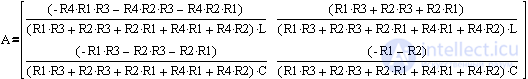
- квадратная матрица второго порядка постоянных коэффициентов при переменных состояния в уравнениях модели.

;

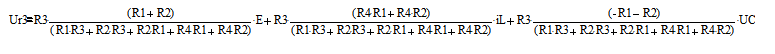
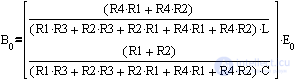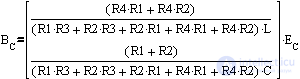
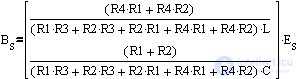
- векторы внешнего воздействия.

Выражение для определения заданной выходной переменной через переменные состояния имеет вид:

Из уравнения (4) находим Ur3

Используя соотношение, 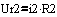переписываем уравнение (23)

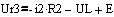(24)

Подставляем значение тока I2 из уравнения (13)

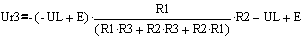(25)

Подставляем значение ULиз уравнения (17)

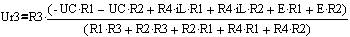(26)

Получаем:

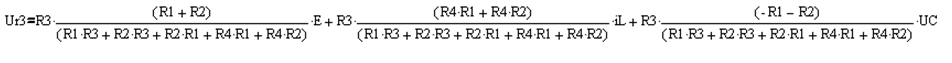
Оптимальная точка

p =0.000100

p =0.006125

kpmax=0.642507

Собственные числа:

l =-1.63277670438401E+0000

l =:-1.47074460251033E+0004

Постоянные времени:

taul= 6.12453618008510E-0001

tau2= 6.79927703486489E-0005

Вау!! 😲 Ты еще не читал? Это зря!

• Моделирование
• Математические основы моделирования систем управления
• моделирование систем управления
• моделирование мехнических систем роцесс

Анализ данных, представленных в статье про моделирование электрических цепей, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое моделирование электрических цепей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем