Метод Эйлера - решения систем обыкновенных дифференциальных уравнений. Уточненный метод Эйлера кратко

Привет, сегодня поговорим про метод эйлера, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое метод эйлера, уточненный метод эйлера , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.

метод эйлера — простейший численный метод решения систем обыкновенных дифференциальных уравнений. Впервые описан Леонардом Эйлером в 1768 году в работе «Интегральное исчисление». Метод Эйлера является явным, одношаговым методом первого порядка точности. Он основан на аппроксимации интегральной кривой кусочно-линейной функцией, так называемой ломаной Эйлера.

Описание метода

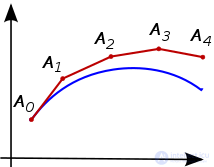
Ломаная Эйлера (красная линия) — приближенное решение в пяти узлах задачи Коши и точное решение этой задачи (выделено синим цветом)

Пусть дана задача Коши для уравнения первого порядка:

где функция определена на некоторой области . Решение ищется на интервале . На этом интервале введем узлы:

Приближенное решение в узлах , которое обозначим через , определяется по формуле:

Эти формулы непосредственно обобщаются на случай систем обыкновенных дифференциальных уравнений.

Оценка погрешности метода на шаге и в целом

Погрешность на шаге или локальная погрешность — это разность между численным решением после одного шага вычисления и точным решением в точке . Численное решение задается формулой

Точное решение можно разложить в ряд Тейлора:

Локальную ошибку получаем, вычитая из второго равенства первое:

Это справедливо, если {\displaystyle y} имеет непрерывную вторую производную . Другим достаточным условием справедливости этой оценки, из которого вытекает предыдущее и которое обычно может быть легко проверено, является непрерывная дифференцируемость по обоим аргументам .

Погрешность в целом, глобальная или накопленная погрешность — это погрешность в последней точке произвольного конечного отрезка интегрирования уравнения. Для вычисления решения в этой точке требуется шагов, где длина отрезка. Поэтому глобальная погрешность метода .

Таким образом, метод Эйлера является методом первого порядка — имеет погрешность на шаге и погрешность в целом .

Значение метода Эйлера

Метод Эйлера являлся исторически первым методом численного решения задачи Коши. Об этом говорит сайт https://intellect.icu . О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.

Характеристика метода Эйлера

• Метод Эйлера является одношаговым методом, то есть для расчета последующей точки необходимо знать только координаты предыдущей.
• Данный метод использует явную схему. В правой части формулы Эйлера стоят все известные величины.
• Метод Эйлера не является устойчивым методом, поэтому он применяется только для ОДУ, решением которых являются достаточно гладкие функции.
• Этот метод характеризуется первым порядком точности (точность низкая).

Модификации и обобщения

Модифицированный метод Эйлера с пересчетом

Повысить точность и устойчивость вычисления решения можно с помощью неявного метода Эйлера следующего вида.

Прогноз:

.

Коррекция:

.

Для повышения точности корректирующую итерацию можно повторить, подставляя .

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо как минимум дважды вычислять . Метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты (предиктор-корректор).

Двухшаговый метод Адамса — Башфорта

Другой способ повысить точность метода заключается в использовании не одного, а нескольких вычисленных ранее значений функции:

Это линейный многошаговый метод.

Реализации на языках программирования

Реализация на языке Си для функции .

#include 

double func(double x, double y)
{
	return 6*x*x+5*x*y; // функция первой производной
}

int main(int argc, char** argv)
{
    int i, n; 
    double x, y, h;

    h = 0.01; // шаг
    n = 10; // количество итераций
    x = 1; // x0
    y = 1; // y0

    for (i = 0; i < n; i++)
    {
        y += h * func(x, y); // вычисление yi
        x += h;
    }

    return EXIT_SUCCESS;
}

Реализация на языке Python 3.7:

# n - количество итераций, h - шаг, (x, y) - начальная точка
def Euler(n = 10, h = 0.01, x = 1, y = 1):
    for i in range(n):
        y += h * function(x, y)
        x += h
    return x, y # решение

def function(x, y):
    return 6 * x**2 + 5 * x * y # функция первой производной

print(Euler())

Улучшенный метод Эйлера

Метод Эйлера для расчета дифференциальных уравнений имеет небольшую точность расчета. Как было показано ранее (см. Лекцию 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера), точность расчета у него зависит от размера шага линейно, зависимость точности от шага — первой степени. То есть, чтобы увеличить точность в 10 раз, надо уменьшить шаг в 10 раз. На практике интересуются более совершенными методами. Вопрос стоит так: можно ли увеличить точность на порядок, но при этом сэкономить на количестве вычислений? Да, такие методы есть. Модифицированный метод Эйлера имеет точность второго порядка. В методе Эйлера производная берется в начале шага и по ней прогнозируется движение системы на конец шага, считая, что во время шага производная неизменна. То есть в течение всего шага производная считается той, какой она была в самом начале шага. Это основной источник неточности.

Улучшение метода состоит в том, что берется производная не в начале шага, а как промежуточное или среднее на разных участках одного шага. В разных вариантах метода вычисляют несколько производных в разных частях шага и усредняют их. Конечно, в этом случае число вычислений увеличивается, — но не в десятки раз, — а вот точность возрастает на порядок, в этом и состоит выигрыш.

Пусть, как и прежде (см. Лекцию 10. Численные методы интегрирования дифференциальных уравнений. Метод Эйлера), требуется решить уравнение y' = f(x, y, t). Идея уточненного метода Эйлера состоит в том, что производную вычисляют не в i-ой точке, а между двумя соседними точками: i иi + 1. Данная процедура состоит из следующих шагов:

• в точке i вычисляют значение производной:
  f(xi, yi, t);
• делают пол-шага и вычисляют значение функции на середине отрезка:
  yi + 1/2 = yi + f(xi, yi, t) · Δt/2;
• в точке i + 1/2 вычисляют производную:
  f(xi + 1/2, yi + 1/2, t + Δt/2);
• делается полный шаг из точки i в точку i + 1 по значению уточненной производной:
  yi + 1 =yi + f(xi + 1/2, yi + 1/2, t + Δt/2) · Δt;
• значение t увеличивается: t := t + Δt. Вся процедура повторяется сначала.

Данный метод обладает точностью Ο2(h), то есть на порядок выше, чем метод Эйлера, при увеличении числа вычислений всего в 2 раза.

На рис. 14.1 показано, какой будет ошибка ε (расхождение между реальным и вычисленным теоретическим значением), если шаг делается по значению производной, вычисленной в точке i, как это делается в методе Эйлера. Эта ошибка может быть достаточно велика!

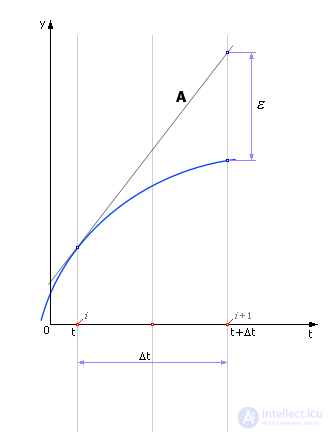
Рис. 14.1. Движение реальной и расчетной системы по методу Эйлера и расхождение между ними (ошибка)

На рис. 14.2 показано, как по значению производной, вычисленной в точке i, делается полшага до точки t + Δt/2 (направление производной показано линией A). И в точке t + Δt/2 вычисляют новую производную. Касательная в точке t + Δt/2 будет другой — линия B. Ее наклон равен производной в точке t + Δt/2.

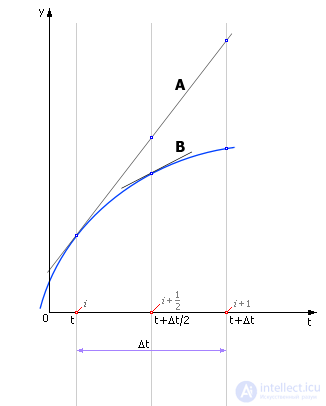
Рис. 14.2. Уточнение значения производной внутри шага расчета

Далее переносят линию B обратно в точку t. Это соответствует тому, что из точки t снова делается, — но уже полный, — шаг Δt до точки t + Δt по направлению, соответствующему линии C(рис. 14.3). Линия C параллельна B. То есть значение производной в точке t берется искусственно равным производной в точке t + Δt/2. Ошибка расчета (см. ε1) во многих случаях при этом уменьшается.

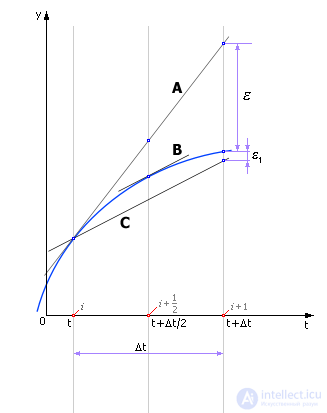
Рис. 14.3. Движение реальной системы и системы, рассчитанной модифицированным методом Эйлера, и расхождение между ними (ошибка). На рисунке для сравнения показан результат, вычисленный по методу Эйлера

Существует другой вариант модифицированного метода Эйлера, когда производную для того, чтобы сделать шаг из точки i, берут не в i-ой точке и не в i + 1/2, а как среднее арифметическое двух производных: производной в точке i (направление производной показано на рис. 14.4 линией A) и производной в точке i + 1 (направление производной показано линией B). Направление «средней» производной показано линией C.

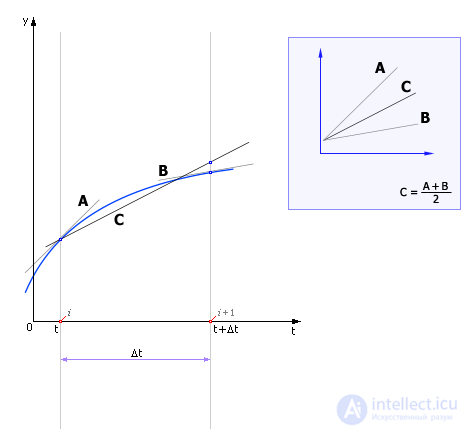
Рис. 14.4. Расчет движения системы по среднему значению производной на шаге

Блок схема и алгоритм метода Эйлера

Решение ОДУ 1-го порядка

Общий вид ОДУ 1-го порядка:

F(x, y, y’)=0

Уравнение разрешаем относительно старшей производной:

y’=f(x, y)

Начальная точка: x0, y0.

Количество точек на интегральной кривой решения n

Шаг h, с которым будет изменяться значение аргумента.

Метод Эйлера

y’=f(x, y)

Представляем производную функции y’ в виде конечной разности.

За величину приращения аргумента Dx принимается величина шага h:

Тогда: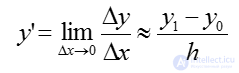

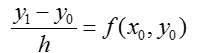
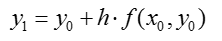
Аналогично: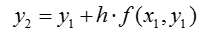

В общем виде: - формула Эйлера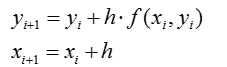

Графическая интерпретация метода Эйлера

Предположим, что мы имеем истинное решение ОДУ: y=y(x).

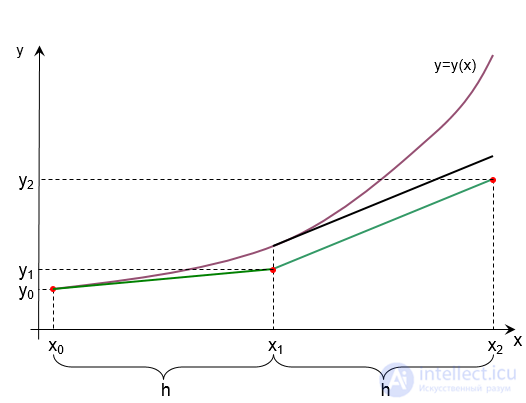
От начальной точки (x0, y0) проводим касательную к графику до пересечения с линией x=x1. Получаем новую точку (x1, y1).

Из графика видно, что с увеличением количества шагов погрешность возрастает.

Если величину шага h уменьшить, то результат получится более точным.

Блок-схема метода Эйлера

Вау!! 😲 Ты еще не читал? Это зря!

• Метод Рунге — Кутты метод рунге-кутты ,
• задача Коши общие понятия дифференциальных уравнений первого порядка , задача коши , дифференциальные уравнения первого порядка , ду первого порядка ,
• метод Адамса
• метод Хенричи
• аппроксимация функций , интерполяция , интерполяция функций , аппроксимация ,

Надеюсь, эта статья об увлекательном мире метод эйлера, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое метод эйлера, уточненный метод эйлера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем