Метод Адамса

Привет, Вы узнаете о том , что такое метод адамса, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое метод адамса , настоятельно рекомендую прочитать все из категории Численные методы.

Ме́тод А́дамса — конечноразностный многошаговый метод численного интегрирования обыкновенных дифференциальных уравнений первого порядка. В отличие от метода Рунге-Кутты использует для вычисления очередного значения искомого решения не одно, а несколько значений, которые уже вычислены в предыдущих точках.

Назван по имени предложившего его в 1855 году английского астронома Джона К. Адамса.

Определение

Пусть дана система дифференциальных уравнений первого порядка

,

для которой надо найти решение на сетке с постоянным шагом . Расчетные формулы метода Адамса для решения этой системы имеют вид:

a) экстраполяционные — метод адамса -Башфорта

,

б) интерполяционные или неявные — метод Адамса-Мультона

,

где — некоторые вычисляемые постоянные.

При одном и том же формула б) точнее , но требует решения нелинейной системы уравнений для нахождения значения . На практике находят приближение из а), а затем приводят одно или несколько уточнений по формуле

.

Свойства

Методы Адамса -го порядка требуют предварительного вычисления решения в начальных точках. Для вычисления начальных значений обычно используют одношаговые методы, например, 4-стадийный метод Рунге — Кутты 4-го порядка точности.

Локальная погрешность методов Адамса -го порядка — . Структура погрешности метода Адамса такова, что погрешность остается ограниченной или растет очень медленно в случае асимптотически устойчивых решений уравнения. Это позволяет использовать этот метод для отыскания устойчивых периодических решений, в частности, для расчета движения небесных тел.

Методы Адамса — Башфорта

Явные методы Адамса — Башфорта

, (метод Эйлера)

Методы Адамса — Мультона

Неявные методы Адамса — Мультона

, (неявный метод Эйлера)

Реализация метода Адамся на языке..

Решение задачи по методу Адамса

Для запуска экстраполяционного метода Адамса требуется 4 начальных значения функции. Об этом говорит сайт https://intellect.icu . Одно значение уже задано, а остальные получаются по методу Рунге-Кутта 4 порядка. После вычисления значения в конце отрезка происходит вычисление относительной погрешности (из текущих и ранее полученных с шагом h значений функции) и сравнение ее с заданным значением. Если полученная погрешность меньше, чем заданная, то считается, что задача выполнена и происходит возврат в вызывающую программу с полученным значением функции. Если же нет – то уменьшается в 2 раза шаг и весь процесс, начиная с метода Рунге-Кутта, повторяется вновь (для вычисления новых значений функции). Так продолжается до тех пор, пока полученное значение погрешности не станет меньше чем заданное.

Для работы программы необходима функция вычисления правых частей системы дифференциальных уравнений. Это функция func (double *y, double *ys, double x). Т. к. в задаче требуется решить уравнение y⁽³⁾+2y’’+3y’+y=5+x², составляем систему дифференциальных уравнений первого порядка. Выглядит она так:

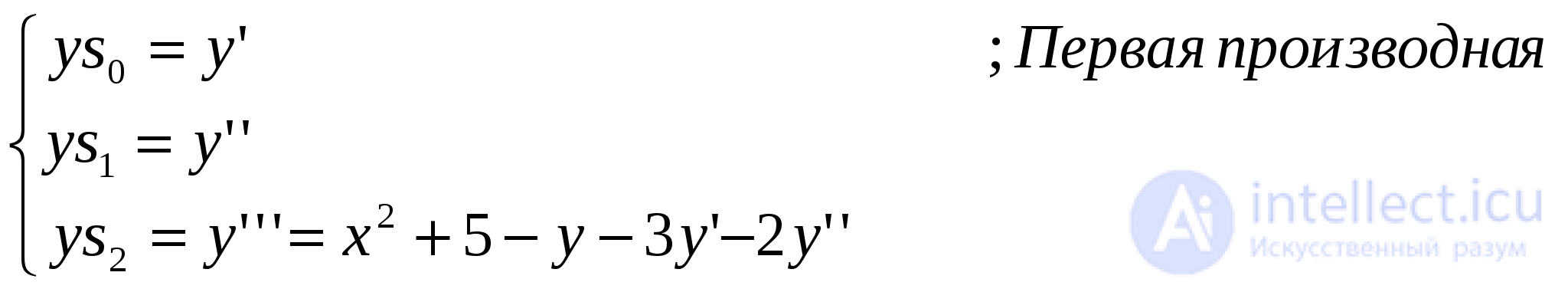
При каждом вычислении левых частей этой системы происходит дифференцирование y, y’ и y’’, т. е. вычисление соответственно новых значений y’, y’’, y’’’.

Ну, а если переложить это все в программу на Си, то получится функция func (смотри листинг 17 задачи).

Блок-схема функции main из программы 17.c

Блок-схема функции Adams из программы 17.c

Листинг программы 17.c

// Задача 17. Численное интегрирование системы дифференциальных уравнений

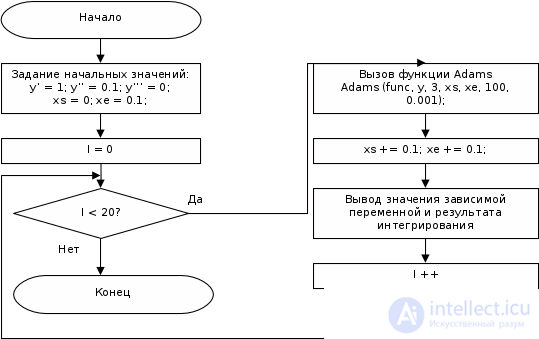
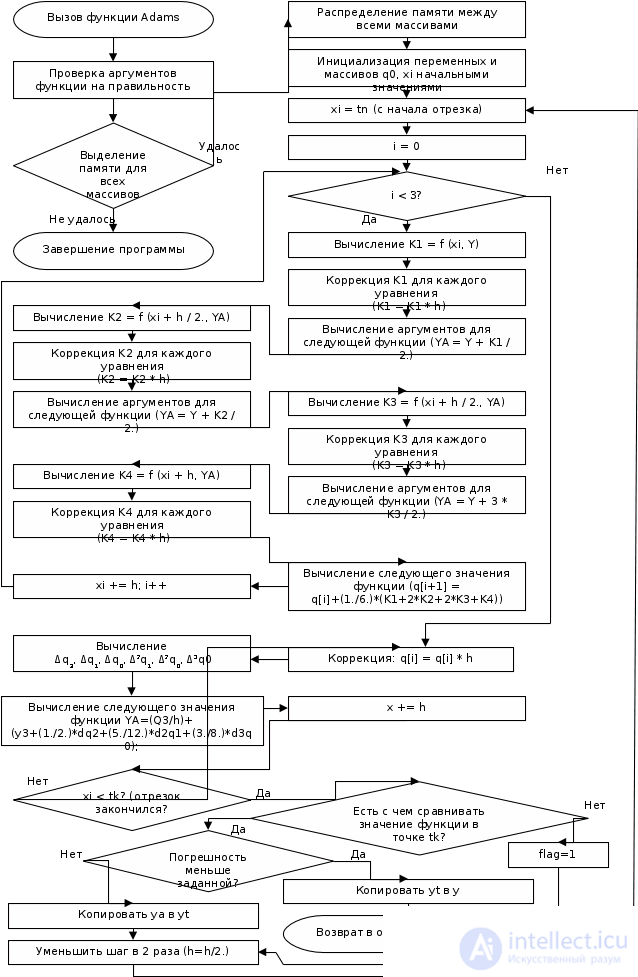
// методом Адамса. Программа рассчитана на компиляцию в Micro$oft C 6.00

// или Borland C 3.1+

// (C) 2004 REPNZ. All rights reserved. Release date is 2.04.2004

#include

#include

#include

void func (double *y, double *ys, double t)

{ // функция вычисления правых частей уравнений

ys = y ; // ys -первая производная; ys -вторая и т.д.

ys = y ; // t-независимый аргумент

ys = 5 + t * t - y - 3. * y - 2. * y ;

}

void Adams (

void f (double *y, double *ys, double x),

// Функция вычиления правых частей системы

double *y, // Массив размера n значений зависимых переменных

int n, // Массив размера n значений производных

double tn, // Начало интервала интегрирования

double tk, // Конец интервала интегрирования

int m, // Начальное число разбиений отрезка интегрирования

double eps) // Относительная погрешность интегрирования

{

double *k1, *k2, *k3, *k4; // Для метода Рунге-Кутта

double *q0, *q1, *q2, *q3; // Значение производных Для метода Адамса

double *ya; // Временный массив

double *y0, *y1, *y2, *y3; // Значения функции для метода Адамса

double h; // Шаг интегрирования

double xi; // Текущее значение независимой переменной

double eps2; // Для оценки погрешности

double dq2, dq1, dq0, d2q1, d2q0, d3q0; // приращения

int flag = 0; // 0, пока идет первый просчет

int i, j; // Индексы

if (m < 4) m = 4; // Минимум 4 отрезка

if (tn >= tk)

{ printf ("\nНеправильные аргументы\n");

abort (); // Неправильные аргументы

}

// Выделяем память для массивов с переменными

if ((k1 = malloc ((4 + 4 + 4 + 1) * n * sizeof (double))) == 0)

{ printf ("\nОшибка распределения памяти\n");

abort (); // Прервать, если не удалось

}

// Распределяем память между массивами:

// Для метода Рунге-Кутта 4 порядка

k2 = k1 + n; k3 = k2 + n; k4 = k3 + n;

// 4 пердыдущих значения функции

y0 = k4 + n; y1 = y0 + n; y2 = y1 + n; y3 = y2 + n;

// Для временного массива сбора данных

ya = y3 + n;

// Для метода Адамса

q0 = ya + n; q1 = q0 + n; q2 = q1 + n; q3 = q2 + n;

h = (tk - tn) / m; // Шаг

eps = fabs (eps); // Абсолютное значение погрешности

start: // Отсюда начинаются вычисления

xi = tn; // Начало промежутка

// Вычисляем значения функции y0...y3, т.е. y[i-3] ... y

// Первое значение системы уравнений уже дано: y ...

///////////////////////////////////////////////////////////////////////

// - Метод Рунге-Кутта 4 порядка - //

///////////////////////////////////////////////////////////////////////

for (j = 0; j < n; j++) y0[j] = y[j]; // Копируем его в y0

f (y0, q0, xi); // Заполняем q0, основываясь на значениях из y0

for (j = 0; j < n; j++) q0[j] *= h; // Делаем q0

xi += h; // Следующий шаг

// ... а остальные 3 добываем с помощью метода Рунге-Кутта 4 порядка.

for (i = 0; i < 3; i++) // i - КАКОЕ ЗНАЧЕНИЕ УЖЕ ЕСТЬ

{ // А ВЫЧИСЛЯЕМ ЗНАЧЕНИЯ Y[i+1]!!!!

// Сначала нужны коэффициенты k1

// Элемент y[i, j] = y0 + (i * n) + j = y0[i * n + j]

f (&y0[i * n], k1, xi); // Вычислим f(xi, yi) = k1 / h

// И для каждого дифференциального уравнения системы проделываем

// операции вычисления k1, а также подготовки в ya аргумента для

// вычисления k2

for (j = 0; j < n; j++)

{

k1[j] *= h; // Вычислим наконец-то k1

ya[j] = y0[i*n+j] + k1[j] / 2.;

// И один из аргументов для функции

} // вычисления k2

f (ya, k2, xi + (h / 2.)); // Вычислим f(xi,yi) = k2 / h

for (j = 0; j < n; j++)

{ // Вычислим наконец-то k2

k2[j] *= h;

ya[j] = y0[i*n+j] + k2[j] / 2.; // И один из аргументов для функции

} // вычисления k3

f (ya, k3, xi + h / 2.); // Вычислим f(xi,yi) = k3 / h

for (j = 0; j < n; j++)

{

k3[j] *= h; // Вычислим наконец-то k3

ya[j] = y0[i*n+j] + k3[j]; // И один из аргументов для функции

} // вычисления k4

f (ya, k4, xi + h); // Вычислим f(xi,yi) = k4 / h

for (j = 0; j < n; j++) k4[j] *= h; // Вычислим наконец-то k4

// Надо вычислить приращение каждой функции из n

for (j = 0; j < n; j++) // Вычисляем следующее значение

// функции

// Y[i+1] = Yi + ...

y0[(i+1)*n+j] = y0[i*n+j] + (k1[j] + 2. * k2[j] + 2 * k3[j] + k4[j]) / 6.;

// И новое значение q[i+1]

f (&y0[(i+1)*n], &q0[(i+1)*n], xi); // qi = f (xi, yi);

for (j = 0; j < n; j++) q0[((i+1)*n)+j] *= h;

xi += h; // Следующий шаг }

///////////////////////////////////////////////////////////////////////

// - Метод Адамса - //

///////////////////////////////////////////////////////////////////////

// Итак, вычислены 4 первых значения. Этого достаточно для начала метода

// Адамса для шага h.

// B y0...y3 лежат 4 значения функций (_НЕ_ПРОИЗВОДНЫХ!!!).

// A в q0...q3 лежат значения _производных_ этих функций, умноженных на h

// q0..q3, а также y0..y3 представляют собой очереди с 4 элементами

again: // Вычисляем новое значение функции Yi (Это Y[i+1])

for (j = 0; j < n; j++)

{ // Все приращения

dq2 = q3[j] - q2[j]; dq1 = q2[j] - q1[j]; dq0 = q1[j] - q0[j];

d2q1 = dq2 - dq1; d2q0 = dq1 - dq0;

d3q0 = d2q1 - d2q0;

// новое значение функции (в ya пока что)

ya[j] = y3[j] + (q3[j] + (dq2 / 2.) + (5. * d2q1 / 12.) + (3. * d3q0 / 8.));

// Сдвигаем все массивы на 1 вперед и добавляем в очередь новое

// значение функции

y0[j] = y1[j]; y1[j] = y2[j]; y2[j] = y3[j]; y3[j] = ya[j];

// Просто сдвигаем q, ничего пока что не добавляя

q0[j] = q1[j]; q1[j] = q2[j]; q2[j] = q3[j];

}

// В очередь в качестве q3 ложим новое значение

f (y3, q3, xi); // q3 = f (xi, y3);

for (j = 0; j < n; j++) q3[j] *= h; // Вычислить q3

// Очередное значение функции вычислено. Следующиий шаг

xi += h;

// Продолжить интегрирование?

if (xi < tk) goto again; // Да.

// Если первый раз здесь, то просчитать еще раз с шагом h/2

if (flag == 0)

flag = 1; // Сравнивать уже будет с чем

else

{

// Не первый раз - оценить погрешность

// Сейчас в y3 - значение только что вычисленной функции ,

// а в y2 - занчение функции, вычисленной с шагом h * 2

// по отношению к текущему

for (j = 0; j < n; j++)

{ eps2 = fabs (((y3[j] - y2[j]) / y2[j]));

if (eps2 > eps) break; // Если погрешность слишком великА

}

if (j == n) // Если все ОК

{ // Копируем результат

for (j = 0; j < n; j++) y[j] = y3[j];

free (k1); // Освобождаем память

return; // Возвращаемся в main

}

}

// По каким-то причинам выхода из функции не произошло -

// тогда уменьшаем шаг в 2 раза и повторяем

// все, начиная с метода Рунге-Кутта

h /= 2.; // Уменьшить шаг

goto start; // Повторить расчет сначала, с новыми параметрами

}

int main ()

{

double y , xs, xe;

int i;

y = 1.; y = 0.1; y = 0.; // Начальные условия

xs = .0; xe = .1; // Начало интегрирования

printf ("x = %5.3lg, y(%4.2lg) = %10.3lg\n", xs, xs, y );

for (i = 0; i < 20; i++)

{

Adams (func, y, 3, xs, xe, 10, 1.e-3);

xs += 0.1; xe += 0.1;

printf ("x = %5.3lg, y(%4.2lg) = %10.3lg\n", xs, xs, y );

}

return 0;

}

Вау!! 😲 Ты еще не читал? Это зря!

• численные методы
• методы прогноза , коррекции итерационные методы метод эйлера , метод милна ,
• метод эйлера , метод усовершенствованного эйлера , метод модифицированного эйлера , численные методы интегрирования дифференциальных уравнений ,
• метод рунге-кутты ,
• дифференциальное уравнение

• метод Эйлера
• метод Хенричи
• метод Милна
• Численные методы решения обыкновенных дифференциальных уравнений
• задача Коши общие понятия дифференциальных уравнений первого порядка , задача коши , дифференциальные уравнения первого порядка , ду первого порядка ,
• Общие линейные методы
• Интегратор групп Ли
• Численное дифференциальное уравнение
• решение дифференциальных уравнений
• дифференциальные уравнения

Исследование, описанное в статье про метод адамса, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое метод адамса и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Численные методы