4. Численное интегрирование

Привет, мой друг, тебе интересно узнать все про численное интегрирование, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое численное интегрирование , настоятельно рекомендую прочитать все из категории Численные методы.

Формулы прямоугольников 
Формула трапеций 
Формула Симпсона

Постановка задачи: Требуется найти значение определенного интеграла 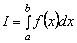 для некоторой заданной на отрезка [a, b] функции f(x). Для некоторых функций значение интеграла можно найти точно. Однако в общем случае значение интеграла можно найти только приближенно, используя тот или иной способ численного интегрирования.

численное интегрирование основано на замене интеграла суммой вида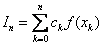. Такая замена следует из определения интеграла как предела суммы 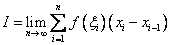. Зафиксировав n, мы получим предыдущую сумму.

Приближенное равенство 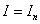 называется квадратурной формулой, 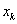- узлы квадратурной формулы,  - коэффициенты квадратурной формулы. Разность 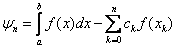называется погрешностью квадратурной формулы.

Разобьем отрезок [a,b] на n частей, точками 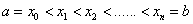. Причем будем рассматривать равномерную сетку, т.е. 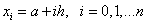. Тогда .

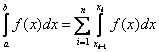Для построения квадратурной формулы на всем отрезке [a,b] достаточно построить квадратурную формулу на частичном отрезке .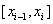

Формулы прямоугольников

Пусть 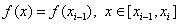, т.е. мы аппроксимируем f(x) левой кусочно–линейной интерполяцией. Тогда получим .

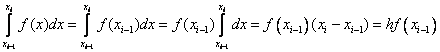Таким образом, 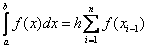. Эта формула называется формулой левых прямоугольников.

Геометрическая интерпретация:

Учитывая, что интеграл от некоторой функции дает значение площади, то площадь криволинейной области заменяется на сумму площадей прямоугольников.

Аналогично получается формула правых прямоугольников. Здесь 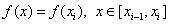. В результате получим: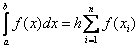 

Оценим погрешность формул. Например, погрешность формулы левых прямоугольников.

.

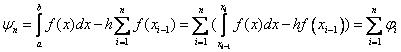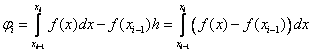
Воспользуемся формулой Тейлора:

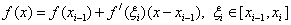
Тогда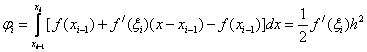 

Пусть 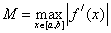, тогда 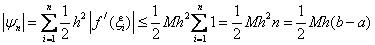,т.е. формула левых прямоугольников имеет первый по h порядок точности.

Аналогично и для формулы правых прямоугольников.

Формула средних прямоугольников. Об этом говорит сайт https://intellect.icu . Здесь функция на отрезке 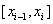 заменяется на ее значение в середине отрезка, т.е.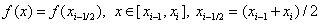 

Тогда, получим 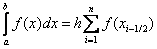 - это формула средних прямоугольников.

Ее удобно записать в виде 

Оценим погрешность формулы средних прямоугольников.

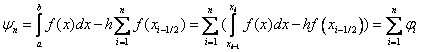
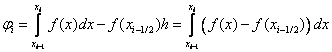
Воспользуемся формулой Тейлора:

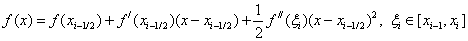
Пусть 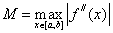, тогда

, т.е. формула средних прямоугольников имеет второй по h порядок точности.

Во всех рассмотренных формулах площадь криволинейной трапеции заменялась на площадь прямоугольников.

Формула трапеций

В этой формуле 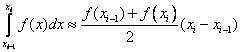, т.е. площадь криволинейной трапеции, заменяется на площадь прямоугольной трапеции.

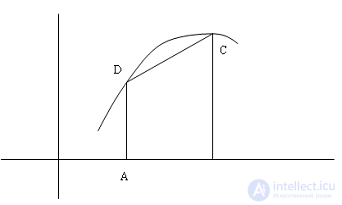
Формула трапеций получается путем замены подынтегральной функции интерполяционным полиномом первой степени:

.

Действительно

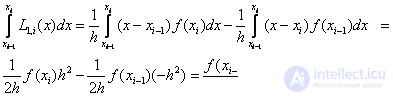
Тогда для всего отрезка [a,b] получим:

Можно показать, что формула трапеций имеет второй порядок точности.

Формулу трапеций можно записать в виде:

Формула Симпсона

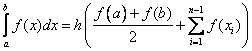
При аппроксимации интеграла 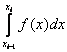, функцию f(x)на отрезке  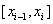заменяют параболой, проходящей через точки 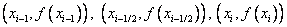, где , т.е. используем для аппроксимации полином Лагранжа второй степени:

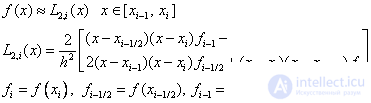
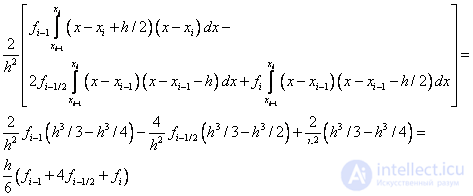
Следовательно, получаем формулу Симпсона

Можно показать, что формула Симпсона имеет четвертый порядок точности.

Пример. Вычислить интеграл 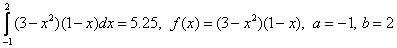. Разобьем отрезок [-1,2] на 10 частей, т.е. 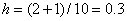. Вычислим значение интеграла по формулам левых, правых, средних прямоугольников, по формуле трапеций и формуле Симпсона. Для этого составим таблицы:

Здесь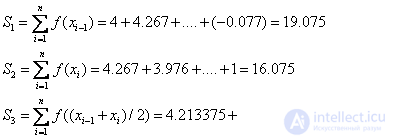 

Формула левых прямоугольников:

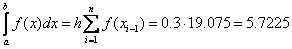
Формула правых прямоугольников:

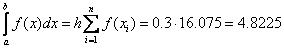
Формула средних прямоугольников:

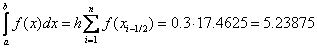
Формула трапеций:

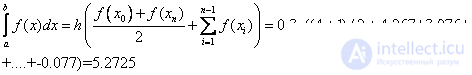
Формула Симпсона:

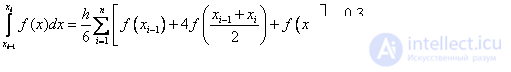
Напомним, что точное значение интеграла 5.25

Я хотел бы услышать твое мнение про численное интегрирование Надеюсь, что теперь ты понял что такое численное интегрирование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Численные методы