Лекция
Привет, мой друг, тебе интересно узнать все про численное решение обыкновенных дифференциальных уравнений, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое численное решение обыкновенных дифференциальных уравнений , настоятельно рекомендую прочитать все из категории Численные методы.
Численные методы решения задачи Коши для ОДУ первого порядка
Численные методы решения систем ОДУ первого порядка
Метод конечных разностей решения краевых задач для ОДУ
Многие задачи науки и техники сводятся к решению обыкновенных дифференциальных уравнений (ОДУ). ОДУ называются такие уравнения, которые содержат одну или несколько производных от искомой функции. В общем виде ОДУ можно записать следующим образом:
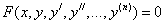 , где x – независимая переменная,
, где x – независимая переменная, 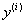 - i-ая производная от искомой функции. n - порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных
- i-ая производная от искомой функции. n - порядок уравнения. Общее решение ОДУ n–го порядка содержит n произвольных постоянных 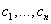 , т.е. общее решение имеет вид
, т.е. общее решение имеет вид 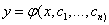 .
.
Для выделения единственного решения необходимо задать n дополнительных условий. В зависимости от способа задания дополнительных условий существуют два различных типа задач: задача Коши и краевая задача. Если дополнительные условия задаются в одной точке, то такая задача называется задачей Коши. Дополнительные условия в задаче Коши называются начальными условиями. Если же дополнительные условия задаются в более чем одной точке, т.е. при различных значениях независимой переменной, то такая задача называется краевой. Сами дополнительные условия называются краевыми или граничными.
Ясно, что при n=1 можно говорить только о задачи Коши.
Примеры постановки задачи Коши:
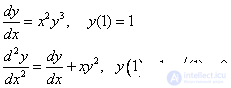
Примеры краевых задач:
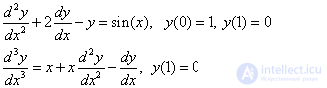
Решить такие задачи аналитически удается лишь для некоторых специальных типов уравнений.
Постановка задачи. Найти решение ОДУ первого порядка
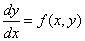 на отрезке
на отрезке 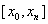 при условии
при условии 
При нахождении приближенного решения будем считать, что вычисления проводятся с расчетным шагом 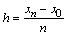 , расчетными узлами служат точки
, расчетными узлами служат точки  промежутка [x0, xn].
промежутка [x0, xn].
Целью является построение таблицы
|
xi |
x0 |
x1 |
… |
xn |
|
yi |
y0 |
y1 |
… |
yn |
т.е. ищутся приближенные значения y в узлах сетки.
Интегрируя уравнение на отрезке  , получим
, получим
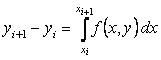
Вполне естественным (но не единственным) путем получения численного решения является замена в нем интеграла какой–либо квадратурной формулой численного интегрирования. Если воспользоваться простейшей формулой левых прямоугольников первого порядка
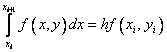 ,
,
то получим явную формулу Эйлера:
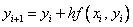 ,
, 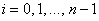 .
.
Порядок расчетов:
Зная 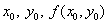 , находим
, находим 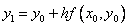 , затем
, затем 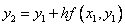 т.д.
т.д.
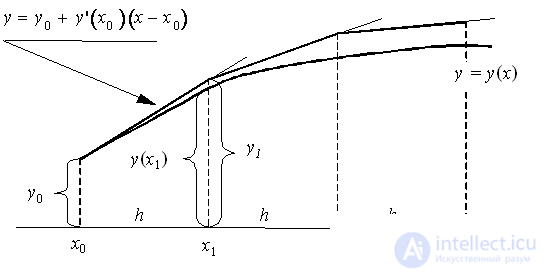
Геометрическая интерпретация метода Эйлера:
Пользуясь тем, что в точке x0 известно решение y(x0) = y0 и значение его производной  , можно записать уравнение касательной к графику искомой функции
, можно записать уравнение касательной к графику искомой функции 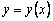 в точке
в точке 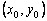 :
: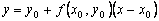 . При достаточно малом шаге h ордината
. При достаточно малом шаге h ордината 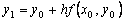 этой касательной, полученная подстановкой в правую часть значения
этой касательной, полученная подстановкой в правую часть значения 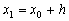 , должна мало отличаться от ординатыy(x1) решения y(x) задачи Коши. Следовательно, точка
, должна мало отличаться от ординатыy(x1) решения y(x) задачи Коши. Следовательно, точка 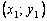 пересечения касательной с прямой x = x1 может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую
пересечения касательной с прямой x = x1 может быть приближенно принята за новую начальную точку. Через эту точку снова проведем прямую 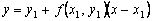 , которая приближенно отражает поведение касательной к
, которая приближенно отражает поведение касательной к 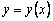 в точке
в точке  . Подставляя сюда
. Подставляя сюда  (т.е. пересечение с прямой x = x2), получим приближенное значение y(x) в точке x2:
(т.е. пересечение с прямой x = x2), получим приближенное значение y(x) в точке x2: 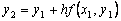 и т.д. В итоге для i–й точки получим формулу Эйлера.
и т.д. В итоге для i–й точки получим формулу Эйлера.
Явный метод Эйлера имеет первый порядок точности или аппроксимации.
Если использовать формулу правых прямоугольников: 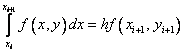 , то придем к методу
, то придем к методу
 ,
, 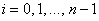 .
.
Этот метод называют неявным методом Эйлера, поскольку для вычисления неизвестного значения 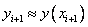 по известному значению
по известному значению  требуется решать уравнение, в общем случае нелинейное.
требуется решать уравнение, в общем случае нелинейное.
Неявный метод Эйлера имеет первый порядок точности или аппроксимации.
Модифицированный метод Эйлера: в данном методе вычисление  состоит из двух этапов:
состоит из двух этапов:

Данная схема называется еще методом предиктор – корректор (предсказывающее – исправляющее). На первом этапе приближенное значение предсказывается с невысокой точностью (h), а на втором этапе это предсказание исправляется, так что результирующее значение имеет второй порядок точности.
Методы Рунге – Кутта: идея построения явных методов Рунге–Кутты p–го порядка заключается в получении приближений к значениям y(xi+1) по формуле вида
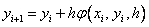 ,
,
где
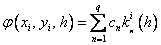
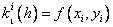
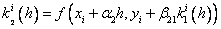
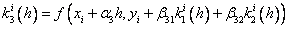
…………………………………………….
 .
.
Здесь an, bnj, pn, 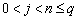 – некоторые фиксированные числа (параметры).
– некоторые фиксированные числа (параметры).
При построения методов Рунге–Кутты параметры функции 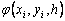 (an, bnj, pn) подбирают таким образом, чтобы получить нужный порядок аппроксимации.
(an, bnj, pn) подбирают таким образом, чтобы получить нужный порядок аппроксимации.
Схема Рунге – Кутта четвертого порядка точности:
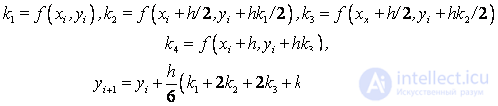
Пример. Решить задачу Коши:
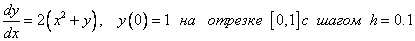 .
.
Рассмотреть три метода: явный метод Эйлера, модифицированный метод Эйлера, метод Рунге – Кутта.
Точное решение: 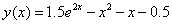
Расчетные формулы по явному методу Эйлера для данного примера:
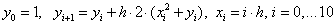
Расчетные формулы модифицированного метода Эйлера:
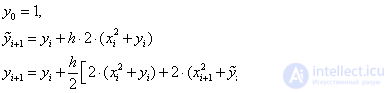
Расчетные формулы метода Рунге – Кутта:
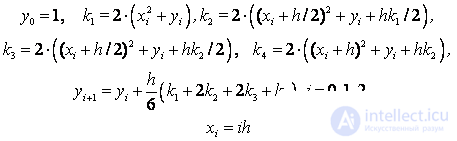
|
x |
y1 |
y2 |
y3 |
точное |
|
0 |
1.0000 |
1.0000 |
1.0000 |
1.0000 |
|
0.1 |
1.2000 |
1.2210 |
1.2221 |
1.2221 |
|
0.2 |
1.4420 |
1.4923 |
1.4977 |
1.4977 |
|
0.3 |
1.7384 |
1.8284 |
1.8432 |
1.8432 |
|
0.4 |
2.1041 |
2.2466 |
2.2783 |
2.2783 |
|
0.5 |
2.5569 |
2.7680 |
2.8274 |
2.8274 |
|
0.6 |
3.1183 |
3.4176 |
3.5201 |
3.5202 |
|
0.7 |
3.8139 |
4.2257 |
4.3927 |
4.3928 |
|
0.8 |
4.6747 |
5.2288 |
5.4894 |
5.4895 |
|
0.9 |
5.7377 |
6.4704 |
6.8643 |
6.8645 |
|
1 |
7.0472 |
8.0032 |
8.5834 |
8.5836 |
y1 – метод Эйлера, y2 – модифицированный метод Эйлера, y3 – метод Рунге Кутта.
Видно, что самым точным является метод Рунге – Кутта.
Рассмотренные методы могут быть использованы также для решения систем дифференциальных уравнений первого порядка.
Покажем это для случая системы двух уравнений первого порядка:
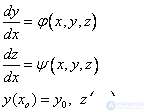
Явный метод Эйлера:
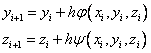
Модифицированный метод Эйлера:

Схема Рунге – Кутта четвертого порядка точности:

К решению систем уравнений ОДУ сводятся также задачи Коши для уравнений высших порядков. Об этом говорит сайт https://intellect.icu . Например, рассмотрим задачу Коши для уравнения второго порядка
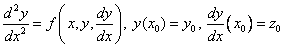
Введем вторую неизвестную функцию 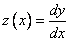 . Тогда задача Коши заменяется следующей:
. Тогда задача Коши заменяется следующей:

Т.е. в терминах предыдущей задачи: 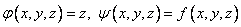 .
.
Пример. Найти решение задачи Коши:
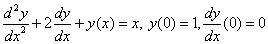 на отрезке [0,1].
на отрезке [0,1].
Точное решение: 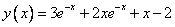
Действительно:

Решим задачу явным методом Эйлера, модифицированным методом Эйлера и Рунге – Кутта с шагом h=0.2.
Введем функцию 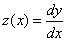 .
.
Тогда получим следующую задачу Коши для системы двух ОДУ первого порядка:
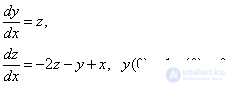
Явный метод Эйлера:
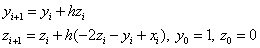
Модифицированный метод Эйлера:

Метод Рунге – Кутта:

Схема Эйлера:
|
X |
y |
z |
y теор |
z теор |
y-y теор |
|
0 |
1 |
0 |
1 |
0 |
0 |
|
0.2 |
1 |
-0.2 |
0.983685 |
-0.14622 |
0.016315 |
|
0.4 |
0.96 |
-0.28 |
0.947216 |
-0.20658 |
0.012784 |
|
0.6 |
0.904 |
-0.28 |
0.905009 |
-0.20739 |
0.001009 |
|
0.8 |
0.848 |
-0.2288 |
0.866913 |
-0.16826 |
0.018913 |
|
1 |
0.80224 |
-0.14688 |
0.839397 |
-0.10364 |
0.037157 |
Модифицированный метод Эйлера:
|
X |
ycv |
zcv |
y |
z |
y теор |
z теор |
y-y теор |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
0.2 |
1 |
-0.2 |
1 |
-0.18 |
0.983685 |
-0.14622 |
0.016315 |
|
0.4 |
0.96 |
-0.28 |
0.962 |
-0.244 |
0.947216 |
-0.20658 |
0.014784 |
|
0.6 |
0.904 |
-0.28 |
0.9096 |
-0.2314 |
0.905009 |
-0.20739 |
0.004591 |
|
0.8 |
0.848 |
-0.2288 |
0.85846 |
-0.17048 |
0.866913 |
-0.16826 |
0.008453 |
|
1 |
0.80224 |
-0.14688 |
0.818532 |
-0.08127 |
0.839397 |
-0.10364 |
0.020865 |
Схема Рунге - Кутта:
|
x |
Y |
z |
k1 |
l1 |
k2 |
l2 |
k3 |
l3 |
k4 |
l4 |
|
0 |
1 |
0 |
0 |
-1 |
-0.1 |
-0.7 |
-0.07 |
-0.75 |
-0.15 |
-0.486 |
|
0.2 |
0.983667 |
-0.1462 |
-0.1462 |
-0.49127 |
-0.19533 |
-0.27839 |
-0.17404 |
-0.31606 |
-0.20941 |
-0.13004 |
|
0.4 |
0.947189 |
-0.20654 |
-0.20654 |
-0.13411 |
-0.21995 |
0.013367 |
-0.2052 |
-0.01479 |
-0.2095 |
0.112847 |
|
0.6 |
0.904977 |
-0.20734 |
-0.20734 |
0.10971 |
-0.19637 |
0.208502 |
-0.18649 |
0.187647 |
-0.16981 |
0.27195 |
|
0.8 |
0.866881 |
-0.16821 |
-0.16821 |
0.269542 |
-0.14126 |
0.332455 |
-0.13497 |
0.317177 |
-0.10478 |
0.369665 |
|
1 |
0.839366 |
-0.1036 |
-0.1036 |
0.367825 |
-0.06681 |
0.40462 |
-0.06313 |
0.393583 |
-0.02488 |
0.423019 |
Max(y-y теор)=4*10-5
Постановка задачи: найти решение линейного дифференциального уравнения
 , (1)
, (1)
удовлетворяющего краевым условиям: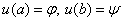 . (2)
. (2)
Теорема. Пусть 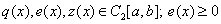 . Тогда существует единственное решение поставленной задачи.
. Тогда существует единственное решение поставленной задачи.
К данной задаче сводится, например, задача об определении прогибов балки, которая на концах опирается шарнирно.
Основные этапы метода конечных разностей:
1) область непрерывного изменения аргумента ([a,b]) заменяется дискретным множеством точек, называемых узлами: 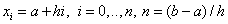 .
.
2) Искомая функция непрерывного аргумента x, приближенно заменяется функцией дискретного аргумента на заданной сетке, т.е. 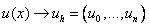 . Функция
. Функция 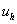 называется сеточной.
называется сеточной.
3) Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции. Такая замена называется разностной аппроксимацией.
Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки, которые находятся из решения алгебраических уравнений.
Аппроксимация производных.
Для аппроксимации (замены) первой производной можно воспользоваться формулами:
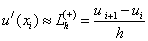 - правая разностная производная,
- правая разностная производная,
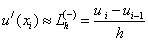 - левая разностная производная,
- левая разностная производная,
 - центральная разностная производная.
- центральная разностная производная.
т.е., возможно множество способов аппроксимации производной.
Все эти определения следуют из понятия производной как предела: 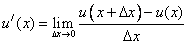 .
.
Опираясь на разностную аппроксимацию первой производной можно построить разностную аппроксимацию второй производной:
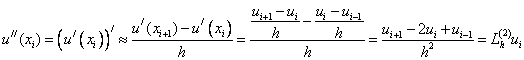 (3)
(3)
Аналогично можно получить аппроксимации производных более высокого порядка.
Определение. Погрешностью аппроксимации n- ой производной называется разность: 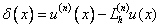 .
.
Для определения порядка аппроксимации используется разложение в ряд Тейлора.
Рассмотрим правую разностную аппроксимацию первой производной:

Т.е. правая разностная производная имеет первый по h порядок аппроксимации.
Аналогично и для левой разностной производной.
Центральная разностная производная имеет второй порядок аппроксимации.
Аппроксимация второй производной по формуле (3) также имеет второй порядок аппроксимации.
Для того чтобы аппроксимировать дифференциальное уравнение необходимо в нем заменить все производные их аппроксимациями. Рассмотрим задачу (1), (2) и заменим в(1) производные:
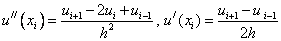 .
.
В результате получим:
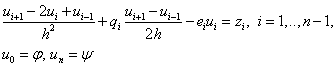 (4)
(4)
Порядок аппроксимации исходной задачи равен 2, т.к. вторая и первая производные заменены с порядком 2, а остальные – точно.
Итак, вместо дифференциальных уравнений (1), (2) получена система линейных уравнений для определения 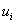 в узлах сетки.
в узлах сетки.
Схему можно представить в виде:

т.е., получили систему линейных уравнений с матрицей:

Данная матрица является трехдиагональной, т.е. все элементы, которые расположены не на главной диагонали и двух прилегающих к ней диагоналях равны нулю.
Решая полученную систему уравнений, мы получим решение исходной задачи.
Для решения таких СЛАУ имеется экономичный метод прогонки.
Рассмотрим метод прогонки для СЛАУ:
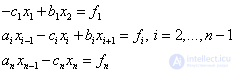 (1)
(1)
Решение данной системы ищем в виде:
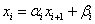 (2)
(2)
Подставляя в первое уравнение, получим:
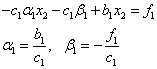
Здесь учтено, что данное соотношение должно выполняться при любом 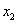
Так как
 , (3)
, (3)
то подставляя (3) во второе уравнение, получим:

Сравнивая с (2) получим
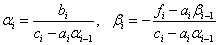 .
.
Таким образом, можно найти все 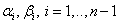 .
.
Тогда из последнего уравнения (1) находим:
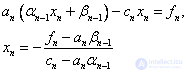
Затем последовательно находим:

Таким образом, алгоритм метода прогонки можно представить в виде:
1) Находим 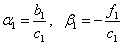
2) Для i=1,n-1: 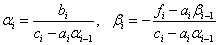 (4)
(4)
3) Находим 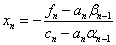
4) Для i=n-1 до 1 находим: 
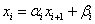
Шаги 1),2) – прямой ход метода прогонки, 3),4) – обратный ход метода прогонки.
Теорема. Пусть коэффициенты ai, bi системы уравнений при i =2, 3, …, n–1 отличны от нуля и пусть
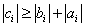 при i =1, 2, 3, …, n. Тогда прогонка корректна и устойчива.
при i =1, 2, 3, …, n. Тогда прогонка корректна и устойчива.
При выполнении этих условий знаменатели в алгоритме метода прогонки не обращаются в нуль и, кроме того, погрешность вычислений, внесенная на каком либо шаге вычислений, не будет возрастать при переходе к следующим шагам. Данное условие есть ни что иное, как условие диагонального преобладания.
Для нашей краевой задачи имеем :

Тогда: 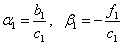 ,
, 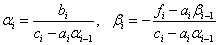 ,
,
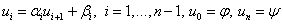
Для нашей задачи условие устойчивости имеет вид:
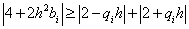 .
.
Пусть
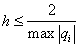 . (6)
. (6)
Тогда 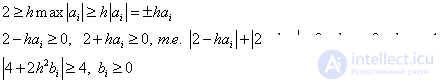
Пример. Найти решение задачи:
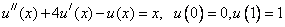
Выпишем разностную схему
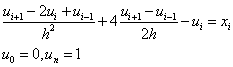
Условие устойчивости примет вид 
Возьмем  .
.
Тогда 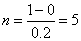
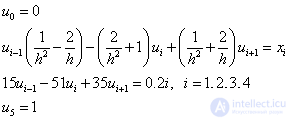
Или

Формулы прогонки были получены для СЛАУ (1):
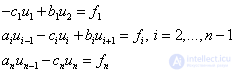
Здесь x замены на u.
Следовательно,
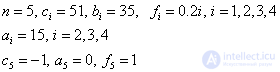
Решим СЛАУ методом прогонки. Вычисления оформим в виде таблицы:
|
I |
ai |
ci |
bi |
fi |
alfai |
betai |
ui |
|
1 |
|
51 |
35 |
0.2 |
0.6863 |
-0.0039 |
0.4701 |
|
2 |
15 |
51 |
35 |
0.4 |
0.8598 |
-0.0113 |
0.6906 |
|
3 |
15 |
51 |
35 |
0.6 |
0.9186 |
-0.0202 |
0.8164 |
|
4 |
15 |
51 |
35 |
0.8 |
0.9403 |
-0.0296 |
0.9107 |
|
5 |
0 |
-1 |
|
1 |
|
|
1.0000 |
Порядок вычислений по формулам (4):
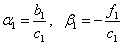
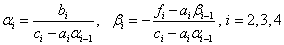

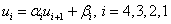
Ответ в столбце ui.
Если забыли формулы, то их можно легко вывести. Главное запомнить основную формулу:
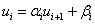

Прямой ход

Обратный ход

На практике часто граничные условия могут иметь более общий вид.
Рассмотрим следующую краевую задачу:
Найти решение ОДУ 2-го порядка
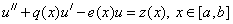 ,
,
удовлетворяющую краевым условиям:

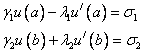
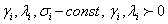
В этом случае при построении разностной схемы необходимо еще аппроксимировать и краевые условия.
Аппроксимация:
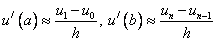
В результате получим разностную схему:
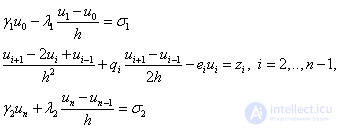
Или
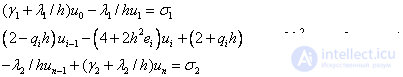
Мы получили СЛАУ типа (5) с трехдиагональной матрицей, решение которой также можно найти методом прогонки.
Я хотел бы услышать твое мнение про численное решение обыкновенных дифференциальных уравнений Надеюсь, что теперь ты понял что такое численное решение обыкновенных дифференциальных уравнений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Численные методы
Комментарии
Оставить комментарий
Численные методы
Термины: Численные методы