Примеры решения задач по численному моделированию кратко

Привет, мой друг, тебе интересно узнать все про задачи численные методы, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое задачи численные методы , настоятельно рекомендую прочитать все из категории Численные методы.

1. Получить решение уравнения f(x)=x³+x²-9x+9=0 методом деления отрезка пополам с точностью 0.05. Интервал изоляции (-4, -3.8)

Проверим, что данный отрезок – интервал изоляции: f(-4)=-3, f(-3.8)=2.768.

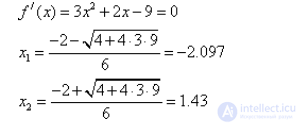
Следовательно,

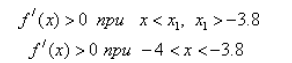
Данный отрезок является интервалом изоляции.

Расчеты

k	a	b	c	f(c)	f(a)	b-a
0	-4	-3.8	-3.9	-3	-0.009	0.2
1	-3.9	-3.8	-3.85	-0.009	1.405875	0.1
2	-3.9	-3.85	-3.875	-0.009	0.705078	0.05
3	-3.9	-3.875	-3.8875	-0.009	0.349705	0.025

Расчетные формулы:

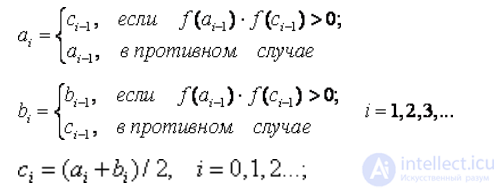
Ответ: x=-3.8875

2. Получить решение уравнения f(x)=x³+x²-9x+9=0 методом простой итерации с точностью 0.001. Интервал изоляции (-5, -3).

Аналогично доказываем, что интервал является интервалом изоляции.

f(-5)=-46, f(-3)=18

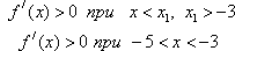
Расчетные формулы:

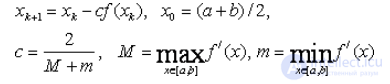
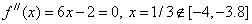
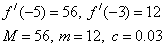
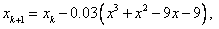
k	x	f(x)	точность
0	-4	-3
1	-3.91	-0.29837	0.09
2	-3.90105	-0.03925	0.008951
3	-3.89987	-0.00529	0.001178
4	-3.89971	-0.00072	0.000159

Ответ: X=-3.8997

3. Об этом говорит сайт https://intellect.icu . Получить решение уравнения f(x)=x³+x²-9x+9=0 методом Ньютона с точностью 0.001. Интервал изоляции (-5, -3).

Расчетные формулы:

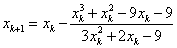
f(-5)= -46, f^//(-5)=6*(-5)+2=-28

Следовательно,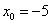

k	x	f(x)	f'(x)	точность
0	-5	-46	56
1	-4.17857	-8.89217	35.02423	0.821429
2	-3.92469	-0.72721	29.36009	0.253886
3	-3.89992	-0.00659	28.82821	0.024769
4	-3.89969	-5.6E-07	28.82332	0.000229

Ответ: x=-3.89969

4. Решить систему линейных уравнений методом простой итерации с точностью 0.05:

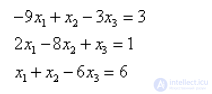
Проверим условие диагонального преобладания:

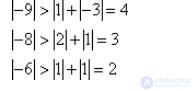
Разрешим систему уравнений относительно x_i

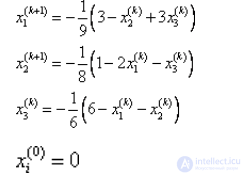
k	x1	x2	x3	точность
0	0	0	0
1	-0.3333333	-0.125	-1	1
2	-0.0138889	-0.33333	-1.07639	0.319444
3	-0.0115741	-0.26302	-1.05787	0.070313
4	-0.0099344	-0.26013	-1.04577	0.012105

5. Решить систему линейных уравнений методом Гаусса–Зейделя с точностью 0.05:

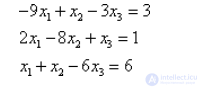
Аналогично проверяем условие диагонального преобладания.

Разрешим систему уравнений относительно x_i

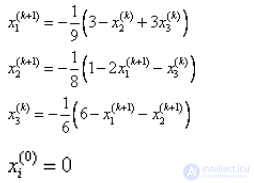
k	x1	x2	x3	точность
0	0	0	0
1	-0.3333333	-0.20833	-1.09028	1.090278
2	0.0069444	-0.25955	-1.0421	0.340278
3	-0.0148052	-0.25896	-1.04563	0.02175

6. Для таблично заданной функции:

x	-2	1	1.5	2
f	0.1	-0.2	0.5	1.2

вычислить значение функции в точке z=1.2, используя формулы линейной интерполяции.

Определяем интервал, которому принадлежит z: [1,1.5].

Расчетные формулы:

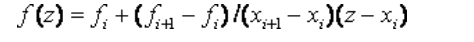
f(z)=-0.2+(0.5+0.2)/(1.5-1)*(1.2-1)= 0.2375.

7. Для таблично заданной функции:

x	-2	1	1.5	2
f	0.1	-0.2	0.5	1.2

выписать базисные полиномы и вычислить значение полинома Лагранжа в точке z=1.2.

n=3.

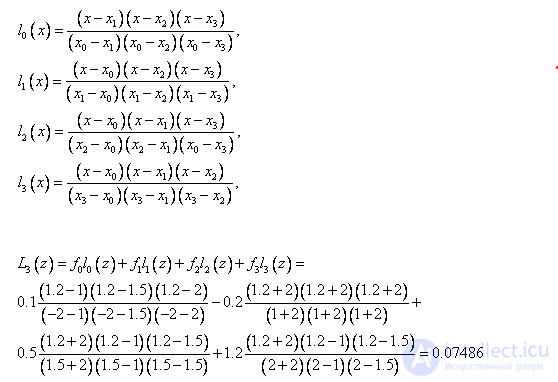
8. Вычислить интеграл методом трапеций для функции, заданной таблично:

В данном задании x меняется с постоянным шагом 0.5

Формула трапеций:

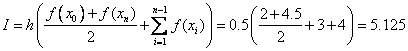
Если шаг не постоянный, например:

то надо пользоваться общей формулой трапеций:

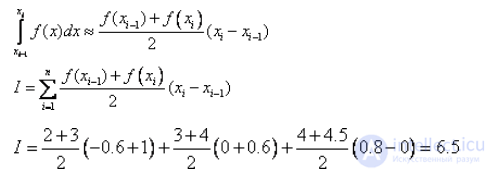
Аналогично для формул левых и правых прямоугольников:

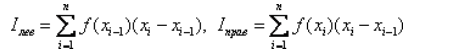
9. Метод наименьших квадратов.

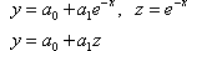
Z	Z1	Z2	...	Zn
y	Y1	Y2	...	Yn

Вау!! 😲 Ты еще не читал? Это зря!

численные методы

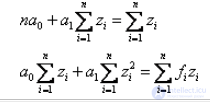
Я хотел бы услышать твое мнение про задачи численные методы Надеюсь, что теперь ты понял что такое задачи численные методы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Численные методы

Из статьи мы узнали кратко, но содержательно про задачи численные методы