2. Методы решения систем линейных алгебраических уравнений

Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени.

В классическом варианте коэффициенты при переменных, свободные члены и неизвестные считаются вещественными числами, но все методы и результаты сохраняются (либо естественным образом обобщаются) на случай любых полей, например, комплексных чисел.

Решение систем линейных алгебраических уравнений — одна из классических задач линейной алгебры, во многом определившая ее объекты и методы. Кроме того, линейные алгебраические уравнения и методы их решения играют важную роль во многих прикладных направлениях, в том числе в линейном программировании, эконометрике.

Могут обобщаться на случай бесконечного множества неизвестных.

Система линейных уравнений от трех переменных определяет набор плоскостей. Точка пересечения является решением

Общий вид системы линейных алгебраических уравнений:

Здесь m — количество уравнений, а n — количество переменных, — неизвестные, которые надо определить, коэффициенты и свободные члены предполагаются известными. Индексы коэффициентов в системах линейных уравнений (aij) формируются по следующему соглашению: первый индекс (i) обозначает номер уравнения, второй (j) — номер переменной, при которой стоит этот коэффициент .

Система называется однородной, если все ее свободные члены равны нулю (b1=b2=⋯=bm=0), иначе — неоднородной.

Квадратная система линейных уравнений — система, у которой количество уравнений совпадает с числом неизвестных (m=n). Система, у которой число неизвестных больше числа уравнений, является недоопределенной, такие системы линейных алгебраических уравнений также называются прямоугольными. Если уравнений больше, чем неизвестных, то система является переопределенной.

Решение системы линейных алгебраических уравнений — совокупность n чисел c1,c2,…,cn, таких что их соответствующая подстановка вместо x1,x2,…,xn в систему обращает все ее уравнения в тождества.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Решения считаются различными, если хотя бы одно из значений переменных не совпадает. Совместная система с единственным решением называется определенной, при наличии более одного решения — недоопределенной.

Система линейных алгебраических уравнений может быть представлена в матричной форме как:

или:

.

Здесь A — это матрица системы, x — столбец неизвестных, а b — столбец свободных членов. Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Теорема Кронекера — Капелли устанавливает необходимое и достаточное условие совместности системы линейных алгебраических уравнений посредством свойств матричных представлений: система совместна тогда и только тогда, когда ранг ее матрицы совпадает с рангом расширенной матрицы.

Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот. Также считается, что системы, не имеющие решений, эквивалентны.

Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений дает систему, эквивалентную исходной.

Система линейных алгебраических уравнений Ax =b эквивалентна системе CAx =Cb, где C — невырожденная матрица. В частности, если сама матрица A — невырожденная, и для нее существует обратная матрица , то решение системы уравнений можно формально записать в виде .

Прямые методы дают алгоритм, по которому можно найти точное решение систем линейных алгебраических уравнений. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

Прямые методы решения СЛАУ:

• Метод Крамера
• Метод обратной матрицы
• Метод Гаусса
• Метод Гаусса — Жордана
• Метод Крамера
• Матричный метод
• Метод прогонки (для трехдиагональных матриц)
• Разложение Холецкого или метод квадратных корней (для положительно-определенных симметричных и эрмитовых матриц)

Итерационные методы решения линейных алгебраических систем:

• Метод простой итерации или метод Якоби
• Метод Гаусса – Зейделя
• Метод Якоби (метод простой итерации)
• Метод Гаусса — Зейделя
• Метод релаксации
• Многосеточный метод
• Метод Монтанте
• Метод Абрамова (пригоден для решения небольших СЛАУ)
• Метод обобщенных минимальных невязок
• Метод бисопряженных градиентов
• Стабилизированный метод бисопряженных градиентов
• Квадратичный метод бисопряженных градиентов
• Метод квази-минимальных невязок (QMR)
• Метод вращений

Итерационные методы устанавливают процедуру уточнения определенного начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения

,

эквивалентного начальной системе линейных алгебраических уравнений. При итерации x в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

.

Итерационные методы делятся на несколько типов, в зависимости от применяемого подхода:

• Основанные на расщеплении:
• Вариационного типа:
• Проекционного типа:

Метод Крамера решения систем линейных алгебраических уравнений

Решение cистем линейных алгебраических уравнений методом обратной матрицы

Исследование неоднородных систем линейных алгебраических уравнений

К решению систем линейных алгебраических уравнений сводятся многочисленные практические задачи ( по некоторым оценкам более 75% всех задач). Можно с полным основанием утверждать, что решение линейных систем является одной из самых распространенных и важных задач вычислительной математики.

Конечно, существует много методов и современных пакетов прикладных программ для решения СЛАУ, но для того, чтобы их успешно использовать, необходимо разбираться в основах построения методов и алгоритмов, иметь представления о недостатках и преимуществах используемых методов.

Постановка задачи

Требуется найти решение системы m линейных уравнений, которая записывается в общем виде как

,

Эту систему уравнений можно записать также в матричном виде:

,

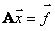где , , .

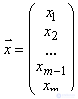A – матрица системы, 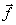– вектор правых частей, – вектор неизвестных.

При известных A и 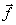требуется найти такие , при подстановке которых в систему уравнений она превращается в тождество.

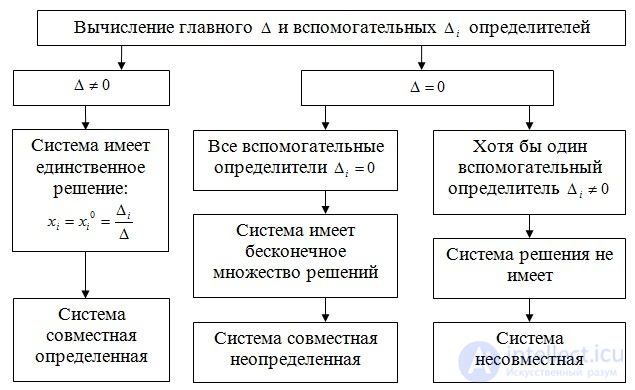
Необходимым и достаточным условием существования единственного решения СЛАУ является условие det A≠0, т.е. определитель матрицы A не равен нулю. В случае равенства нулю определителя матрица A называется вырожденной и при этом СЛАУ либо не имеет решения, либо имеет их бесчисленное множество.

В дальнейшем будем предполагать наличие единственного решения.

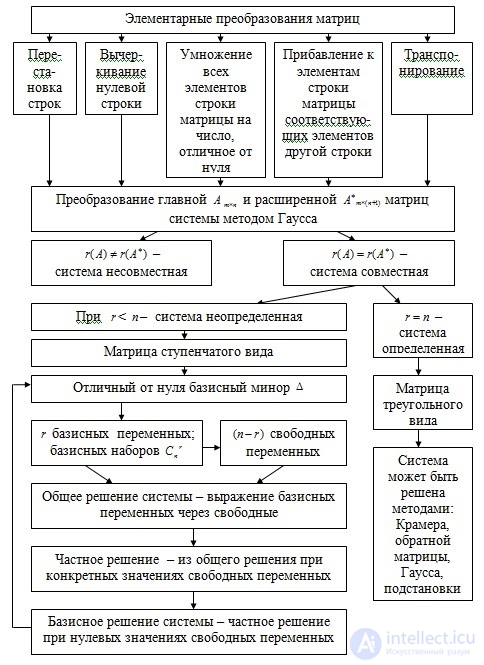
Все методы решения линейных алгебраических задач можно разбить на два класса: прямые (точные) и итерационные (приближенные).

Прямые методы решения СЛАУ

Метод Крамера

При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:

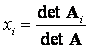(i = 1, 2, …, m). Эти формулы позволяют находить неизвестные в виде дробей, знаменателем которых является определитель матрицы системы, а числителем – определители матриц Ai, полученных из A заменой столбца коэффициентов при вычисляемом неизвестном столбцом свободных членов. Так А1 получается из матрицы А заменой первого столбца на столбец правых частей f.

Например, для системы двух линейных уравнений

Размерность системы (т.е., число m) является главным фактором, из–за которого формулы Крамера не могут быть использованы для численного решения СЛАУ большого порядка. При непосредственном раскрытии определителей решение системы с m неизвестными требует порядка m!*m арифметических операций. Таким образом, для решения системы, например, из m = 100 уравнений потребуется совершить 10158 вычислительных операций (процесс займет примерно 1019 лет), что не под силу даже самым мощным современным ЭВМ

Метод обратной матрицы

Если det A ≠ 0, то существует обратная матрица 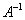. Тогда решение СЛАУ записывается в виде: . Следовательно, решение СЛАУ свелось к умножению известной обратной матрицы на вектор правых частей. Таким образом, задача решения СЛАУ и задача нахождения обратной матрицы связаны между собой, поэтому часто решение СЛАУ называют задачей обращения матрицы. Проблемы использования этого метода те же, что и при использовании метода Крамера: нахождение обратной матрицы – трудоемкая операция.

Метод Гаусса

Наиболее известным и популярным прямым методом решения СЛАУ является метод Гаусса. Этот метод заключается в последовательном исключении неизвестных. Пусть в системе уравнений

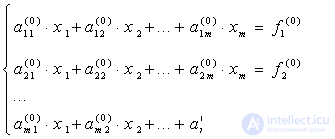
первый элемент 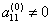. Назовем его ведущим элементом первой строки. Поделим все элементы этой строки на и исключим x1 из всех последующих строк, начиная со второй, путем вычитания первой (преобразованной), умноженной на коэффициент при в соответствующей строке. Получим

.

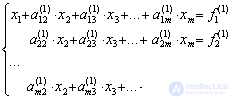Если 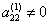, то, продолжая аналогичное исключение, приходим к системе уравнений с верхней треугольной матрицей

.

Из нее в обратном порядке находим все значения xi:

.

Процесс приведения к системе с треугольной матрицей называется прямым ходом, а нахождения неизвестных – обратным. В случае если один из ведущих элементов равен нулю, изложенный алгоритм метода Гаусса неприменим. Кроме того, если какие–либо ведущие элементы малы, то это приводит к усилению ошибок округления и ухудшению точности счета. Поэтому обычно используется другой вариант метода Гаусса – схема Гаусса с выбором главного элемента. Путем перестановки строк, а также столбцов с соответствующей перенумерацией коэффициентов и неизвестных добиваются выполнения условия:

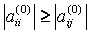, j = i+1,i+ 2, …, m;

т.е. осуществляется выбор первого главного элемента. Переставляя уравнения так, чтобы в первом уравнении коэффициент a11 был максимальным по модулю. Разделив первую строку на главный элемент, как и прежде, исключают x1 из остальных уравнений. Затем для оставшихся столбцов и строк выбирают второй главный элемент и т.д.

Рассмотрим применение метода Гаусса с выбором главного элемента на примере следующей системы уравнений:

В первом уравнении коэффициент при =0, во втором = 1 и в третьем = -2, т.е. максимальный по модулю коэффициент в третьем уравнении. Поэтому переставим третье и первое уравнение:

Исключим из второго и третьего уравнений с помощью первого. Во втором уравнении исключать не надо. Для исключения из третьего уравнения умножим первое на 0.5 и сложим с третьим:

Рассмотрим второе и третье уравнения. Максимальный по модулю элемент при 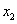в третьем. Поэтому поместим его на место второго:

Исключим 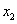из третьего уравнения. Для этого умножим второе на -0.5 и сложим с третьим:

Обратный ход: .

Проверка: 0.5*8+0=4, -3+8-0=5, -2*(-3)+0=6.

Такая перестановка уравнений необходима для того, чтобы уменьшить влияние ошибок округления на конечный результат.

Часто возникает необходимость в решении СЛАУ, матрицы которые являются слабо заполненными, т.е. содержат много нулевых элементов. В то же время эти матрицы имеют определенную структуру. Среди таких систем выделим системы с матрицами ленточной структуры, в которых ненулевые элементы располагаются на главной диагонали и на нескольких побочных диагоналях. Для решения систем с ленточными матрицами коэффициентов вместо метода Гаусса можно использовать более эффективные методы. Например, метод прогонки, который мы рассмотрим позже при решении краевой задачи для обыкновенного дифференциального уравнения второго порядка.

Итерационные методы решения линейных алгебраических систем

Метод простой итерации или метод Якоби

Напомним, что нам требуется решить систему линейных уравнений, которая в матричном виде записывается как:

,

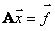где , , .

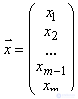Предположим, что диагональные элементы матриц A исходной системы не равны 0 (aii ≠ 0, i = 1, 2, …, n). Разрешим первое уравнение системы относительно x1, второе относительно x2 и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:

(1),

Теперь, задав нулевое приближение , по рекуррентным соотношениям (1) можем выполнять итерационный процесс, а именно:

(2)

Аналогично находятся следующие приближения , где в (2) вместо необходимо подставить .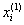

Или в общем случае:

. (3)

или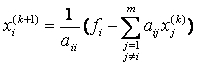

Условие окончания итерационного процесса .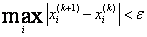

Достаточное условие сходимости: Если выполнено условие диагонального преобладания, т.е. 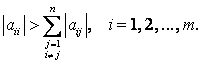, то итерационный процесс (3) сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.

Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут или .

Замечание. Указанное выше условие сходимости является достаточным, т.е. если оно выполняется, то процесс сходится. Однако процесс может сходиться и при отсутствии диагонального преобладания, а может и не сойтись.

Пример.

Решить систему линейных уравнений с точностью :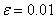

	8	4	2		10		x1
=	3	5	1	=	5	=	x2
	3	–2	10		4		x3

Решение прямыми методами, например, обратной матрицей, дает решение:

.

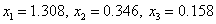Найдем решение методом простой итерации. Проверяем условие диагонального преобладания: , , .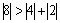

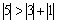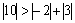Приводим систему уравнений к виду (1):

.

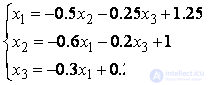Начальное приближение 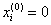. Дальнейшие вычисления оформим в виде таблицы:

k	x1	x2	x3	точность
0	0	0	0
1	1.250	1.000	0.400	1.2500
2	0.650	0.170	0.225	0.8300
3	1.109	0.565	0.239	0.4588
	………
4	0.908	0.287	0.180	0.2781
5	1.061	0.419	0.185	0.1537
6	0.994	0.326	0.165	0.0931
7	1.046	0.370	0.167	0.0515
8	1.023	0.594	0.160	0.2235
9	0.913	0.582	0.212	0.1101
10	0.906	0.505	0.242	0.0764
11	0.937	0.495	0.229	0.0305
12	0.945	0.516	0.218	0.0210
	……
13	0.937	0.523	0.220	0.0077

Здесь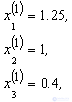

,

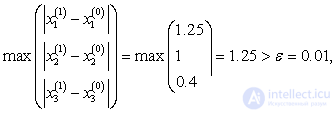
И т.д., пока не получим, в последнем столбце величину меньшую 0.01, что произойдет на 13 – ой итерации.

Следовательно, приближенное решение имеет вид: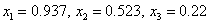

Метод Гаусса – Зейделя

Расчетные формулы имеют вид:

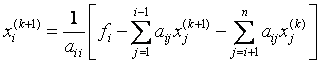
т.е. для подсчета i–й компоненты (k+1)–го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1)–м шаге, новые значения первых i–1 компонент.

Подробные формулы имеют вид:

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение:

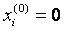
Найдем решение предыдущей системы уравнений методом Гаусса – Зейделя.

Расчетные формулы:

k	x1	x2	x3	точность
0	0	0	0
1	1.250	0.250	0.075	1.2500
2	1.106	0.321	0.132	0.1438
3	1.056	0.340	0.151	0.0500
4	1.042	0.344	0.156	0.0139
5	1.039	0.346	0.157	0.0036

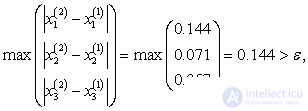
Из таблицы видно, что нужная точность достигнута уже на 5–ой итерации вместо 13–ой по методу простой итерации и значения корней более близки к значениям, полученным методом обратной матрицы.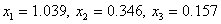

Практическое прмернение систем алгебрачическх уравнений

Системы линейных алгебраических уравнений (СЛАУ) широко применяются для моделирования и решения задач, где требуется найти значения множества переменных, связанных линейными соотношениями. Вот основные области и задачи, в которых они находят свое применение:

1. Физика и инженерия

• Статика и динамика конструкций: В инженерии СЛАУ применяются для анализа балок, мостов и других конструкций, где необходимо учитывать множество сил и моментов, действующих на систему, чтобы рассчитать напряжения и деформации.
• Электротехнические расчеты: При анализе сложных электрических цепей с множеством узлов (метод Кирхгофа) составляются системы линейных уравнений для вычисления токов и напряжений в каждом элементе цепи. Такие расчеты необходимы при проектировании электронных схем и сетей.

2. Экономика и финансы

• Оптимизация и планирование ресурсов: СЛАУ используются для решения задач линейного программирования и оптимизации ресурсов, например, для минимизации затрат при производстве или увеличении прибыли. Эти задачи помогают планировать производство, распределение и управление запасами.
• Анализ экономических моделей: В макроэкономике и финансовом анализе системы линейных уравнений применяются для моделирования взаимосвязей между такими факторами, как потребление, производство, занятость и инвестиции.

3. Компьютерная графика

• Трансформации и анимация объектов: В графике и компьютерной визуализации СЛАУ используются для преобразования координат объектов, поворота, масштабирования и перемещения в пространстве. Это позволяет формировать и изменять сложные трехмерные сцены.
• Рендеринг и освещение: Для расчета освещения и отбрасывания теней при моделировании сцены часто решаются системы линейных уравнений, описывающие пути света и взаимодействие с поверхностями.

4. Робототехника и управление

• Управление движением и траекторией: В робототехнике СЛАУ используются для вычисления траекторий движения роботов и манипуляторов. Система уравнений помогает рассчитать углы поворота и положение суставов робота для достижения заданной позиции.
• Системы управления процессами: В задачах управления, где требуется отслеживать параметры в реальном времени, линейные системы позволяют быстро вычислять корректирующие воздействия на управляющие сигналы, что важно для стабилизации и контроля процессов.

5. Анализ данных и машинное обучение

• Регрессия и модели прогнозирования: В статистике и машинном обучении системы линейных уравнений применяются для построения регрессионных моделей, которые помогают находить линейные зависимости между переменными и делать прогнозы на основе данных.
• Метод наименьших квадратов: Этот метод, который позволяет минимизировать ошибку предсказания, также сводится к решению системы линейных уравнений, где параметры модели определяются как решения такой системы.

6. Геофизика и экология

• Моделирование потоков и распределения загрязнителей: В геофизике СЛАУ применяются для моделирования потоков подземных вод, перемещения загрязняющих веществ и тепловых потоков. Такие модели помогают предсказывать распространение загрязнений и изменение температурных полей.
• Климатическое моделирование: В климатологии системы линейных уравнений используются для моделирования движения воздуха и воды, что позволяет прогнозировать погодные условия и изменения климата.

7. Химия и биология

• Расчет химического равновесия: В химии СЛАУ применяются для вычисления концентраций веществ в реакции, особенно когда системы находятся в равновесии. В задачах типа баланса массы составляются системы уравнений для описания равновесных концентраций веществ.
• Генетические исследования и модели популяций: В биологии линейные системы используются для моделирования популяционной динамики, например, чтобы анализировать взаимодействие между популяциями в экосистемах.

8. Социальные науки

• Социальные и экономические сети: В социологии и экономике системы линейных уравнений применяются для моделирования сетей и связей, описывающих взаимодействия и влияние в группах. Например, линейные модели могут анализировать влияние одной группы на другую.
• Анализ данных из анкет и опросов: Системы уравнений помогают обрабатывать большие объемы данных, собранных в результате опросов, находя общие зависимости и корреляции между факторами, такими как возраст, доход и место жительства.

9. Системы рекомендаций и интернет-аналитика

• Рекомендательные системы: В интернете и маркетинге СЛАУ используются для создания систем рекомендаций, которые предлагают пользователю товары или услуги, основываясь на его предпочтениях и предпочтениях других пользователей.
• Анализ социальных сетей: Системы линейных уравнений помогают анализировать связи и распространение информации в социальных сетях, например, для оценки влияния одного пользователя на других.

---

Системы линейных уравнений представляют собой универсальный инструмент, применяемый для анализа и моделирования самых разных задач, что делает их незаменимыми в научных исследованиях, бизнесе и повседневной практике.

Вау!! 😲 Ты еще не читал? Это зря!

• квадратное уравнение , ax² + bx + c a ≠ 0 , теорема виета , уравнение второй степени ,
• кубическое уравнение ,
• линейное уравнение ,