Метод Рунге-Кутты как класс численных методов решения задачи Коши, блок-схема и примеры решений и реализации

Привет, сегодня поговорим про метод рунге-кутты, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое метод рунге-кутты , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.

Методы Рунге — Кутты (в литературе встречаются названия: методы Рунге — Кутта или же методы Рунге — Кутта) — большой класс численных методов решения задачи Коши для обыкновенных дифференциальных уравнений и их систем. Первые методы данного класса были предложены около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении. Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты

К классу методов Рунге — Кутты относятся явный метод Эйлера и модифицированный метод Эйлера с пересчетом, которые представляют собой соответственно методы первого и второго порядка точности. Существуют стандартные явные методы третьего порядка точности, не получившие широкого распространения. Наиболее часто используется и реализован в различных математических пакетах (Maple, MathCAD, Maxima) классический метод Рунге — Кутты, имеющий четвертый порядок точности. При выполнении расчетов с повышенной точностью все чаще применяются методы пятого и шестого порядков точности. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями .

Методы седьмого порядка должны иметь по меньшей мере девять стадий, а методы восьмого порядка — не менее 11 стадий. Для методов девятого и более высоких порядков (не имеющих, впрочем, большой практической значимости) неизвестно, сколько стадий необходимо для достижения соответствующего порядка точности

метод рунге-кутты используют для расчета стандартных моделей достаточно часто, так как при небольшом объеме вычислений он обладает точностью метода Ο4(h).

Для построения разностной схемы интегрирования воспользуемся разложением функции

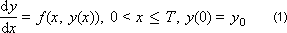
в ряд Тейлора:

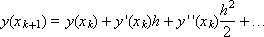
Заменим вторую производную в этом разложении выражением

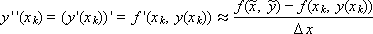
где

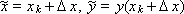
Причем Δx подбирается из условия достижения наибольшей точности записанного выражения. Для дальнейших выкладок произведем замену величины «y с тильдой» разложением в ряд Тейлора:

Для исходного уравнения (1) построим вычислительную схему:

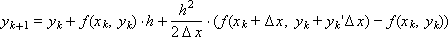
которую преобразуем к виду:

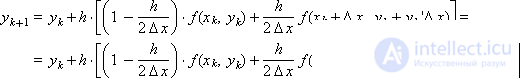
Введем следующие обозначения:

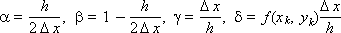
Эти обозначения позволяют записать предыдущее выражение в форме:

Очевидно, что все введенные коэффициенты зависят от величины Δx и могут быть определены через коэффициент α, который в этом случае играет роль параметра:

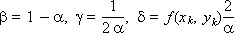
Окончательно схема Рунге-Кутты принимает вид:

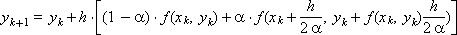
Та же схема в форме разностного аналога уравнения (1):

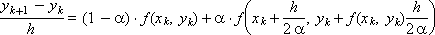
При α = 0 получаем как частный случай уже известную схему Эйлера:

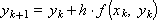
При α = 1:

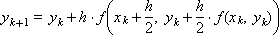
При α = 1 проведение расчетов на очередном шаге интегрирования можно рассматривать как последовательность нижеследующих операций.

1. Вычисляется выражение, представляющее собой полушаг интегрирования по схеме Эйлера, то есть определяется приближенное значение искомой функции в точке xk + h/2:

   

2. Для той же промежуточной точки находится приближенное значение производной:

   

3. Определяется уточненное значение функции в конечной точке всего шага, причем по схеме Эйлера с вычисленным на предыдущем шаге значением производной:

   

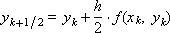
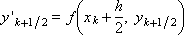
Геометрические построения (см. рис. 15.1) показывают, что получаемое в такой последовательности решение лежит «ближе» к истинному, чем вычисляемое по схеме Эйлера, то есть следует ожидать более высокой точности решения, получаемого методом Рунге-Кутты. Ранее мы назвали эту схему «модифицированным методом Эйлера».

Рис. 15.1. Иллюстрация расчета на шаге методом Рунге-Кутты при значении параметра α = 1

Теперь рассмотрим схему при α = 0.5 (геометрическая интерпретация результата приведена нарис. 15.2).

1. Выполняется полный шаг метода Эйлера с целью определения приближенного значения искомой функции на конце отрезка интегрирования:

   

2. Для этой же точки вычисляется приближенное значение производной:

   

3. Находится среднее значение двух производных, определенных на концах отрезка:

   

4. Вычисляется значение искомой функции в конечной точке всего шага по схеме Эйлера с усредненным значением производной:

   

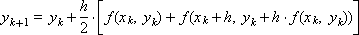
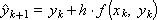
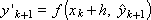
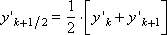
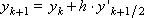
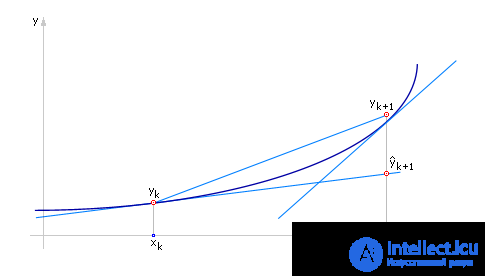
Рис. 15.2. Иллюстрация расчета на шаге методом Рунге-Кутты при значении параметра α = 0.5

Иногда получающееся выражение называют схемой (методом) Эйлера-Коши. Геометрически понятно, что получаемый указанным способом результат также должен быть «ближе» к истинному решению, чем получаемый по схеме Эйлера.

Пример. Решить уравнение dy/dx = –y, y(0) = 1 методом Рунге-Кутты.

Поскольку правая часть дифференциального уравнения имеет вид: f(x, y) = –y, схема метода приα = 0.5 представляется следующим образом:

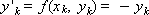
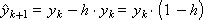
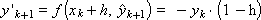
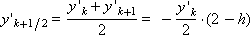
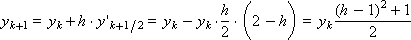
Построим последовательность значений искомой функции:

…

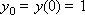
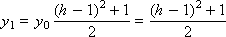
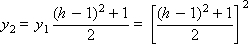
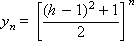
Pезультаты получаемого численного решения для значения аргумента x = 10 при различных шагах интегрирования приведены в табл. 15.1. Три верные значащие цифры получены для шага h = 0.01.

Таблица 15.1. Результаты численного решения yn методом Рунге-Кутты второго порядка дифференциального уравнения y' = –y с начальным условием y(0) = 1

Величина шага h	0.5	0.25	0.1	0.01	0.001	0.0001
Число шагов n	20	40	100	1000	10 000	100 000
yn · 104	0.827181	0.514756	0.462229	0.454076	0.454000	0.453999

Оценим погрешность аппроксимации уравнения (1) разностной схемой метода Рунге-Кутты. Подставляем точное решение в разностный аналог исходного дифференциального уравнения и вычисляем невязку:

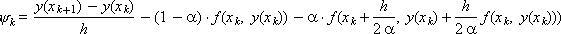
Подставим разложения функций

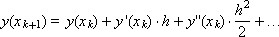
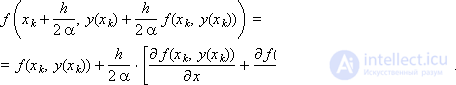
в полученное выражение:

Учитывая уравнение (1), а также выражение для производной

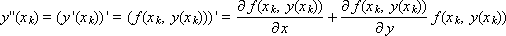
окончательно получаем, что ψk = Ο(h2), то есть метод Рунге-Кутты, независимо от значения параметраα, имеет второй порядок аппроксимации.

Методы Рунге-Кутты третьего и четвертого порядков

Рассмотрим две различные схемы Рунге-Кутты, предназначенные для численного решения обыкновенных дифференциальных уравнений первого порядка и имеющие третий порядок аппроксимации:

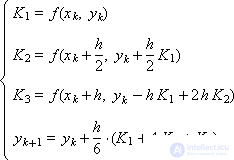
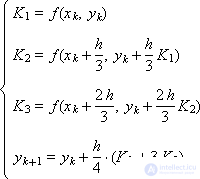
И две схемы Рунге-Кутты, имеющие четвертый порядок аппроксимации:

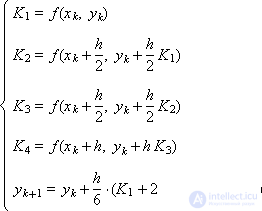
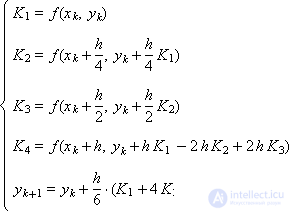
Пример. Об этом говорит сайт https://intellect.icu . Решить методом Рунге-Кутты четвертого порядка уравнение dy/dx = –y, y(0) = 1.

В соответствии с приведенными выше соотношениями определяем коэффициенты:

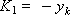
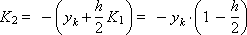
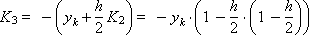
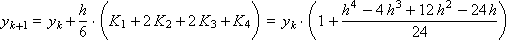
Построим последовательность значений искомой функции:

…

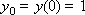
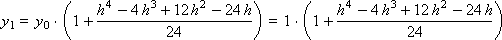
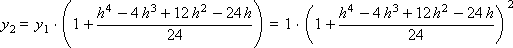
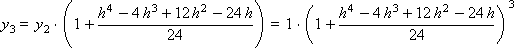
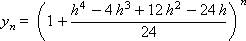
Результаты получаемого численного решения для значения аргумента x = 10 при различных шагах интегрирования приведены в табл. 15.2. Три верные значащие цифры получены для шагаh = 0.25.

Таблица 15.2. Результаты численного решения yn методом Рунге-Кутты четвертого порядка дифференциального уравнения y' = –y с начальным условием y(0) = 1

Величина шага h	0.5	0.25	0.1	0.01	0.001	0.0001
Число шагов n	20	40	100	1000	10 000	100 000
yn · 104	0.457608	0.454181	0.454003	0.453999	0.453999	0.453999

---

Сравнение таблиц 15.1 и 15.2 с решениями одной и той же задачи позволяет сделать вывод, чтоболее высокая степень аппроксимации дифференциального уравнения разностным аналогом позволяет получать более точное решение при более крупном шаге и, следовательно, меньшем числе шагов, то есть приводит к снижению требуемых ресурсов ЭВМ.

На сегодняшний день для грубого расчета вычисления производятся методом Эйлера, для точного расчета — методом Рунге-Кутты.

Классический метод Рунге — Кутты четвертого порядка

Метод Рунге — Кутты четвертого порядка при вычислениях с постоянным шагом интегрирования столь широко распространен, что его часто называют просто методом Рунге — Кутты.

Рассмотрим задачу Коши для системы обыкновенных дифференциальных уравнений первого порядка. (Далее , а ).

Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

Вычисление нового значения проходит в четыре стадии:

где {\displaystyle h} — величина шага сетки по {\displaystyle x}.

Этот метод имеет четвертый порядок точности. Это значит, что ошибка на одном шаге имеет порядок , а суммарная ошибка на конечном интервале интегрирования имеет порядок .

Явные методы Рунге — Кутты

Семейство явных методов Рунге — Кутты является обобщением как явного метода Эйлера, так и классического метода Рунге — Кутты четвертого порядка. Оно задается формулами

где — величина шага сетки по и вычисление нового значения проходит в этапов:

{

Конкретный метод определяется числом и коэффициентами и . Эти коэффициенты часто упорядочивают в таблицу (называемую таблицей Бутчера):

Для коэффициентов метода Рунге — Кутты должны быть выполнены условия для . Если требуется, чтобы метод имел порядок , то следует также обеспечить условие

где — приближение, полученное по методу Рунге — Кутты. После многократного дифференцирования это условие преобразуется в систему полиномиальных уравнений относительно коэффициентов метода.

Неявные методы Рунге — Кутты

Все до сих пор упомянутые методы Рунге — Кутты являются явными методами . К сожалению, явные методы Рунге — Кутты, как правило, непригодны для решения жестких уравнений из-за малой области их абсолютной устойчивости. Неустойчивость явных методов Рунге — Кутты создает весьма серьезные проблемы и при численном решении дифференциальных уравнений в частных производных[en].

Неустойчивость явных методов Рунге — Кутты мотивировала развитие неявных методов. Неявный метод Рунге — Кутты имеет вид

где

Явный метод характерен тем, что матрица коэффициентов для него имеет нижний треугольный вид (включая и нулевую главную диагональ) — в отличие от неявного метода, где матрица имеет произвольный вид. Это также видно по таблице Батчера[en].

Следствием этого различия является необходимость на каждом шагу решать систему уравнений для , где {\displaystyle s} — число стадий. Это увеличивает вычислительные затраты, однако при достаточно малом можно применить принцип сжимающих отображений и решать данную систему методом простой итерации . В случае одной итерации это увеличивает вычислительные затраты всего лишь в два раза.

С другой стороны, Жан Кунцма́н (1961) и Джон Батчер (1964) показали, что при любом количестве стадий {\displaystyle s} существует неявный метод Рунге — Кутты с порядком точности . Это значит, например, что для описанного выше явного четырехстадийного метода четвертого порядка существует неявный аналог с вдвое большим порядком точности.

Неявный метод Рунге — Кутты второго порядка

Простейшим неявным методом Рунге — Кутты является модифицированный метод Эйлера «с пересчетом». Он задается формулой:

.

Для его реализации на каждом шаге необходимы как минимум две итерации (и два вычисления функции).

Прогноз:

.

Коррекция:

.

Вторая формула — это простая итерация решения системы уравнений относительно }, записанной в форме сжимающего отображения. Для повышения точности итерацию-коррекцию можно сделать несколько раз, подставляя . Модифицированный метод Эйлера «с пересчетом» имеет второй порядок точности.

Устойчивость

Преимуществом неявных методов Рунге — Кутты в сравнении с явными является их бо́льшая устойчивость, что особенно важно при решении жестких уравнений. Рассмотрим в качестве примера линейное уравнение y' = λy. Обычный метод Рунге — Кутты, примененный к этому уравнению, сведется к итерации , с r, равным

где обозначает вектор-столбец из единиц . Функция называется функцией устойчивости Из формулы видно, что является отношением двух полиномов степени , если метод имеет стадий. Явные методы имеют строго нижнюю треугольную матрицу откуда следует, что и что функция устойчивости является многочленом

Численное решение данного примера сходится к нулю при условии с . Множество таких называется областью абсолютной устойчивости. В частности, метод называется A-устойчивым, если все с находятся в области абсолютной устойчивости. Функция устойчивости явного метода Рунге — Кутты является многочленом, поэтому явные методы Рунге — Кутты в принципе не могут быть A-устойчивыми

Если метод имеет порядок , то функция устойчивости удовлетворяет условию при . Таким образом, представляет интерес отношение многочленов данной степени, приближающее экспоненциальную функцию наилучшим образом. Эти отношения известны как аппроксимации Паде. Аппроксимация Паде с числителем степени и знаменателем степени А-устойчива тогда и только тогда, когда

-стадийный метод Гаусса — Лежандра имеет порядок , поэтому его функция устойчивости является приближением Паде . Отсюда следует, что метод является A-устойчивым . Это показывает, что A-устойчивые методы Рунге — Кутты могут иметь сколь угодно высокий порядок. В отличие от этого, порядок А-устойчивости методов Адамса не может превышать два.

Произношение

Согласно грамматическим нормам русского языка, фамилия Ку́тта склоняется, поэтому говорят: «Метод Ру́нге — Ку́тты». Правила русской грамматики предписывают склонять все фамилии (в том числе и мужские), оканчивающиеся на -а, -я, которым предшествует согласный. Единственное исключение — фамилии французского происхождения с ударением на последнем слоге типа Дюма́, Золя́ . Однако иногда встречается несклоняемый вариант «Метод Ру́нге — Ку́тта»

Пример решения на алгоритмических языках программирования

производя замену и перенося {\displaystyle 4y} в правую часть, получаем систему:

код на Java для решения системы дифференциальных уравнений методом Рунге-Кутты

public class MainClass {

	public static void main(String[] args) {
		int k = 2;
		double Xo, Yo, Y1, Zo, Z1;
		double k1, k2, k4, k3, h;
		double q1, q2, q4, q3;
                /*
                 *Начальные условия
                 */
		Xo = 0;
		Yo = 0.8;
                Zo = 2;

		h = 0.1; // шаг

		System.out.println("\tX\t\tY\t\tZ");
		for(; r(Xo,2)<1.0; Xo += h){
			
			k1 = h * f(Xo, Yo, Zo);
			q1 = h * g(Xo, Yo, Zo);
			
			k2 = h * f(Xo + h/2.0, Yo + q1/2.0, Zo + k1/2.0);
			q2 = h * g(Xo + h/2.0, Yo + q1/2.0, Zo + k1/2.0);
			
			k3 = h * f(Xo + h/2.0, Yo + q2/2.0, Zo + k2/2.0);
			q3 = h * g(Xo + h/2.0, Yo + q2/2.0, Zo + k2/2.0);
			
			k4 = h * f(Xo + h, Yo + q3, Zo + k3);
			q4 = h * g(Xo + h, Yo + q3, Zo + k3);
			
			Z1 = Zo + (k1 + 2.0*k2 + 2.0*k3 + k4)/6.0;
			Y1 = Yo + (q1 + 2.0*q2 + 2.0*q3 + q4)/6.0;
			System.out.println("\t" + r(Xo + h, k) + "\t\t" + r(Y1 ,k) + "\t\t" + r(Z1 ,k));
			Yo = Y1;
			Zo = Z1;
		}
		
	}
        /**
         * функция для округления и отбрасывания "хвоста"
         */
	public static double r(double value, int k){
		return (double)Math.round((Math.pow(10, k)*value))/Math.pow(10, k);
	}
        /**
         * функции, которые получаются из системы
         */
	public static double f(double x, double y, double z){
		return (Math.cos(3*x) - 4*y);
	}
	public static double g(double x, double y, double z){
		return (z);
	}

}

Код на языке C#

using System;
using System.Collections.Generic;

namespace PRJ_RungeKutta
{
    /// 

/// Реализация метода Ру́нге — Ку́тты для обыкновенного дифференциального уравнения ///

public abstract class RungeKutta { ///

/// Текущее время ///

public double t; ///

/// Искомое решение Y — само решение, Y[i] — i-я производная решения ///

public double[] Y; ///

/// Внутренние переменные ///

double[] YY, Y1, Y2, Y3, Y4; protected double[] FY; ///

/// Конструктор ///

///размерность системы public RungeKutta(uint N) { Init(N); } ///

/// Конструктор ///

public RungeKutta(){} ///

/// Выделение памяти под рабочие массивы ///

///Размерность массивов protected void Init(uint N) { Y = new double[N]; YY = new double[N]; Y1 = new double[N]; Y2 = new double[N]; Y3 = new double[N]; Y4 = new double[N]; FY = new double[N]; } ///

/// Установка начальных условий ///

///Начальное время ///Начальное условие public void SetInit(double t0, double[] Y0) { t = t0; if (Y == null) Init((uint)Y0.Length); for (int i = 0; i < Y.Length; i++) Y[i] = Y0[i]; } ///

/// Расчет правых частей системы ///

///текущее время ///вектор решения /// правая часть abstract public double[] F(double t, double[] Y); ///

/// Следующий шаг метода Рунге-Кутта ///

///текущий шаг по времени (может быть переменным) public void NextStep(double dt) { int i; if (dt < 0) return; // рассчитать Y1 Y1 = F(t, Y); for (i = 0; i < Y.Length; i++) YY[i] = Y[i] + Y1[i] * (dt / 2.0); // рассчитать Y2 Y2 = F(t + dt / 2.0, YY); for (i = 0; i < Y.Length; i++) YY[i] = Y[i] + Y2[i] * (dt / 2.0); // рассчитать Y3 Y3 = F(t + dt / 2.0, YY); for (i = 0; i < Y.Length; i++) YY[i] = Y[i] + Y3[i] * dt; // рассчитать Y4 Y4 = F(t + dt, YY); // рассчитать решение на новом шаге for (i = 0; i < Y.Length; i++) Y[i] = Y[i] + dt / 6.0 * (Y1[i] + 2.0 * Y2[i] + 2.0 * Y3[i] + Y4[i]); // рассчитать текущее время t = t + dt; } } class TMyRK : RungeKutta { public TMyRK(uint N) : base(N) { } ///

/// пример математический маятник /// y''(t)+y(t)=0 ///

///Время ///Решение /// Правая часть public override double[] F(double t, double[] Y) { FY = Y ; FY = -Y ; return FY; } ///

/// Пример использования ///

static public void Test() { // Шаг по времени double dt = 0.001; // Объект метода TMyRK task = new TMyRK(2); // Определим начальные условия y(0)=0, y'(0)=1 задачи double[] Y0 = { 0, 1 }; // Установим начальные условия задачи task.SetInit(0, Y0); // решаем до 15 секунд while (task.t <= 15) { Console.WriteLine("Time = {0:F5}; Func = {1:F8}; d Func / d x = {2:F8}", task.t, task.Y , task.Y ); // вывести t, y, y' // рассчитать на следующем шаге, шаг интегрирования task.NextStep(dt); } Console.ReadLine(); } } class Program { static void Main(string[] args) { TMyRK.Test(); } } }

В программе на С# используется абстрактный класс RungeKutta, в котором следует переопределить абстрактный метод F, задающий правые части уравнений.

Пример решения в среде MATLAB

Решение систем дифференциальных уравнений методом Рунге — Кутты является одним из самых распространенных численных методов решений в технике. В среде MATLAB реализована его одна из разновидностей — метод Дормана — Принса[en]. Для решения системы уравнений необходимо сначала записать функцию, вычисляющую производные, т. е. функции y = g(x, y, z) и z = cos(3x) − 4y = f(x, y, z), о чем сказано выше.

Решение систем дифференциальных уравнений методом Рунге-Кутты является одним из наиболее распространенных численных методов решения в технике. В среде MATLAB / Octave (достаточно распространенная и удобная язык программирования для технических вычислений) реализован один из его разновидностей - метод Дорманда-Принса.

В одном из каталогов, к которому имеется доступ из системы MATLAB, нужно создать текстовый файл с именем (например) runge.m со следующим содержимым (для MATLAB версии 5.3):

MATLAB, runge.m

function Dy = runge(x, y)
Dy = y(:);
Dy(1) = y(2);
Dy(2) = cos(3*x) - 4*y(1);

Имя файла и имя функции должно совпадать, но оно может быть любым неиспользуемым ранее.

Затем необходимо создать главный файл c именем, например, main.m, который будет выполнять основные вычисления. Этот главный файл будет содержать следующий текст:

MATLAB, main.m

clear; clc; % Очистка памяти и экрана
h = 0.1; % Шаг интегрирования
x_fin = 8; % Конечное время интегрирования
y0 = 0.8; % Начальное значение функции
Dy0 = 2; % Начальное значение производной функции
[x, y] = ode45('runge', [0:h:x_fin], [y0 Dy0]); % Метод Рунге — Кутты
plot(x, y, 'LineWidth', 2); grid; % Построение графика и сетки
legend('y(x)', 'y''(x)', 0); % Легенда на графике

Так как MATLAB ориентирован на работу с матрицами, решение по методу Рунге — Кутты очень легко выполняется для целого ряда x как, например, в приведенном примере программы. Здесь решение — график функции в пределах времен от 0 до x_fin.

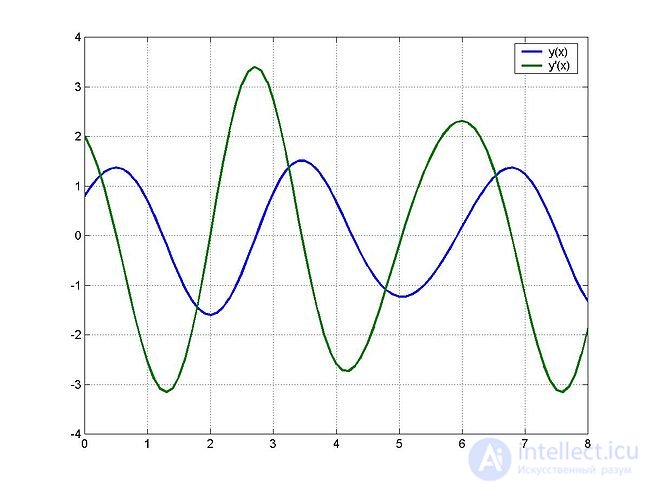
Решение в среде MATLAB

Переменные x и y, полученные в результате работы функции ODE45, есть векторы значений. Очевидно, что решение конкретно заданного выше примера — второй элемент x, так как первое значение 0, шаг интегрирование h = 0,1, а интересуемое значение x = 0,1. Следующая запись в командном окне MATLAB даст искомое решение:

MATLAB, решение

y1 = y(find(x == 0.1))

Ответ: y1 = 0,98768

Блок-схема алгоритма Метода Рунге-Кутта 4 порядка

Данный метод 4-й порядок точности, является одношаговым, имеет явную схему, но не всегда устойчив.

Для реализации этого метода используются достаточно громоздкие формулы Рунге-Кутта:

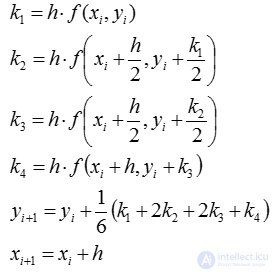
Несмотря на сложные формулы, данный метод является самым распространенным.

Пример реализации

Вау!! 😲 Ты еще не читал? Это зря!

• численные методы
• методы прогноза , коррекции итерационные методы метод эйлера , метод милна ,
• метод эйлера , метод усовершенствованного эйлера , метод модифицированного эйлера , численные методы интегрирования дифференциальных уравнений ,
• дифференциальное уравнение

• метод Эйлера
• метод адамса ,
• метод Хенричи
• метод Милна
• Численные методы решения обыкновенных дифференциальных уравнений
• задача Коши общие понятия дифференциальных уравнений первого порядка , задача коши , дифференциальные уравнения первого порядка , ду первого порядка ,
• Общие линейные методы
• Интегратор групп Ли
• Численное дифференциальное уравнение
• решение дифференциальных уравнений
• дифференциальные уравнения

Надеюсь, эта статья об увлекательном мире метод рунге-кутты, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое метод рунге-кутты и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем