Привет, Вы узнаете о том , что такое размерности применяемые в клеточных автоматах, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
размерности применяемые в клеточных автоматах , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
Для оценки площади произвольной области можно использовать простой
прибор – палетку – прозрачную пластинку с нанесенной на нее квадратной сеткой.
Если подсчитать число квадратов сетки, целиком попавших внутрь области, то
получим оценку площади снизу, если подсчитать количество квадратов, полностью
покрывших область – оценка сверху.
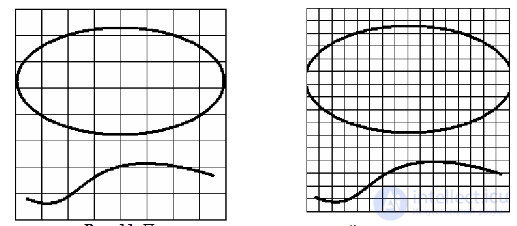
Очевидно, что чем меньше размер квадрата, тем точнее оценка. Если оценивать
площадь некоторой области пространства при уменьшении линейного размера
квадрата ε, число квадратов возрастет как N(ε) ≅ 1/(ε)^2 , если же рассматривать не
область, а кривую, то N(ε)≅1/(ε) (рис. 11).
Рис. 11. При уменьшении размера ячейки точность возрастает
Обобщая эти соотношения, получим:
 , где D – размерность
, где D – размерность
исследуемого множества. Об этом говорит сайт https://intellect.icu . Размерность выступает как число, характеризирующее
скорость роста числа ячеек покрытия данного множества при уменьшении размера
ячейки. Далее логарифмируем и устремляем ε к нулю:
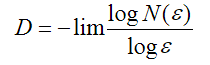
(3)
Понятно, что размерность линии, высчитанная по этой формуле будет равна 1,
размерность плоскости – 2, размерность объема – 3. Вообще размерность
«привычных» нам объектов выражается целым числом. Но, оказывается, можно
построить такие объекты, размерность которых будет дробной.
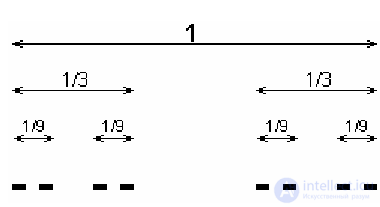
Для примера исследуем канторово множество, которое строится следующим
образом: единичный отрезок делится на три равные части и средняя часть
выбрасывается, далее все повторяется для оставшихся двух частей и т.д. В итоге
имеем такую картину (рис 12):
Рис 12. Канторово множество
Такое множество называется фрактальным. Для оценки размерности этого
множества в качестве ячеек ε возьмем интервалы длины ε
. Как видно из построения, покрытие интервалами длины ε = 1/3 содержит два элемента, при
ε = 1/9 – четыре элемента, и так далее при ε = (1/3)^k ( количество элементов будет 2^k . Тогда по
формуле размерности имеем:
Это дробное число! Следует отметить, что размерность фрактальных множеств
в общем случае дробна. Подробнее о размерности смотрите в [11].
11. Ахромеева Т.С. и др. Нестационарные структуры и диффузионный хаос, М. 1991
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области размерности применяемые в клеточных автоматах имеет потенциал
для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое размерности применяемые в клеточных автоматах
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Моделирование и Моделирование систем
Из статьи мы узнали кратко, но содержательно про размерности применяемые в клеточных автоматах
 , где D – размерность
, где D – размерность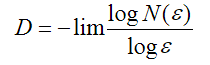 (3)
(3)
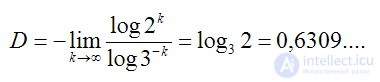
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем