Методы поиска стационарных решений кратко

Привет, Вы узнаете о том , что такое методы поиска стационарных решений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое методы поиска стационарных решений, стационарное решение, стационарный режим, стационарное движение, установившиеся движения , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.

При реализации математических моделей электрических цепей проблема поиска стационарных решений систем дифференциальных уравнений одна из центральных. Это объясняется тем, что стационарные решения описывают установившиеся состояния, которые для электрических цепей являются обычными состояниями функционирования.

Стационарное состояние в теории динамических систем — это такое состояние системы или процесса, в котором динамика переменных, описывающих поведение системы или процесса и называемых переменными состояниями, не меняется во времени (в отличие от переходного процесса). Синонимы: стационарное решение , стационарный режим , стационарное движение , установившиеся движения

Стационарное движение есть предельное движение системы, то есть то, к которому система стремится; причем состояние покоя также рассматривается как частный случай стационарного движения.Именно стационарные движения системы являются наиболее характерными для поведения системы в течение длительных промежутков времени.

Принято различать устойчивое и неустойчивое стационарное состояние.

Примерами стационарных состояний могут служить: фокус, узел, седло, предельный цикл.

Решение системы дифференциальных уравнений, удовлетворяющее начальным условиям X(t₀)=Q,будем обозначатьX(t, t₀ , Q).

В настоящем пособии рассмотрим методы поиска стационарных решений нормальных систем линейных неоднородных дифференциальных уравнений первого порядка с постоянными коэффициентами и внешним периодическим воздействием.

Решение таких систем имеет вид

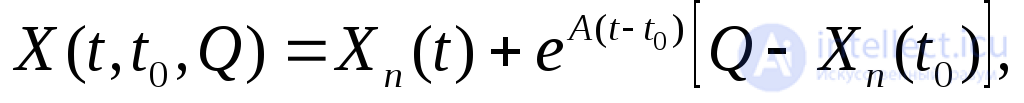(2.17)

где X_n(t) -стационарное решение периодического типа, представляющее собой частное решение системы неоднородных дифференциальных уравнений.

1. Аналитический метод

Характер частного решения системы линейных неоднородных дифференциальных уравнений определяется характером внешнего воздействия нацель.

Пусть внешнее воздействие является периодическим и имеет вид:

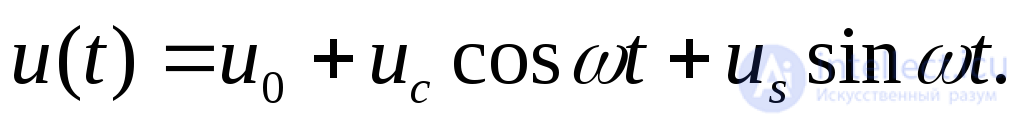(2.18)

В этом случае систему дифференциальных уравнений (2.17) можно представить в виде:

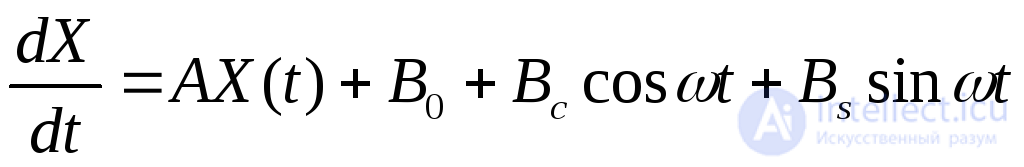(2.19)

где B₀ -вектор внешних воздействий, соответствующий слагаемомуU₀;

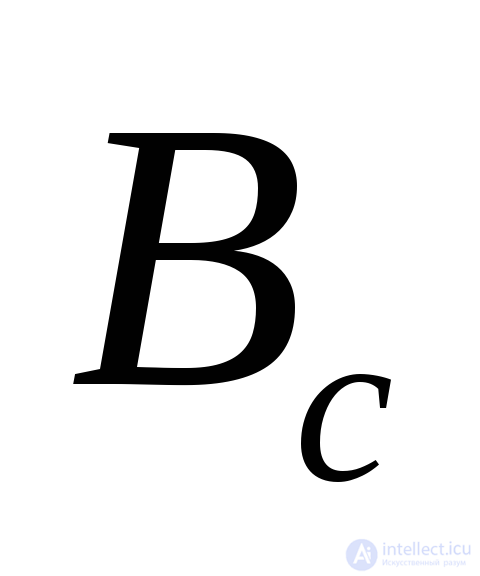- вектор внешних воздействий, соответствующий слагаемому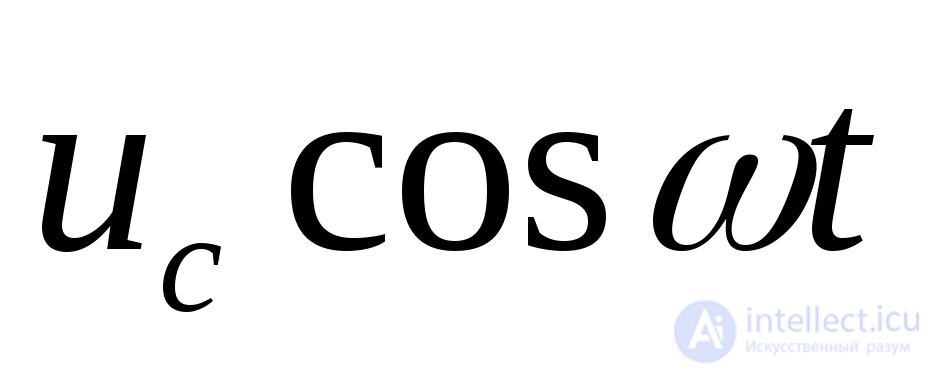; 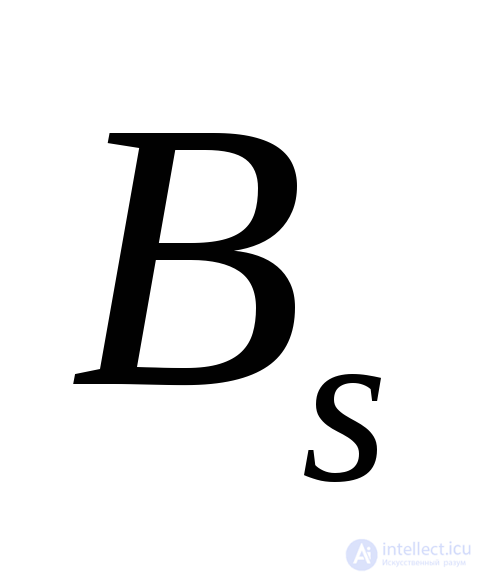-вектор внешних воздействий, соответствующий слагаемому .

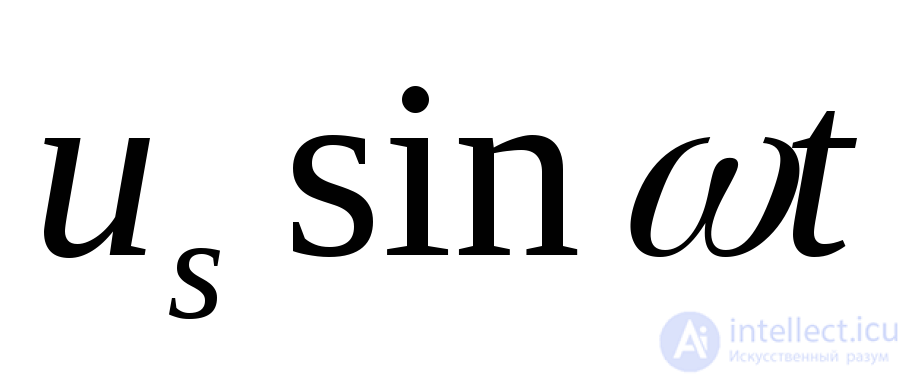Частное решение данной системы уравнений имеет вид:

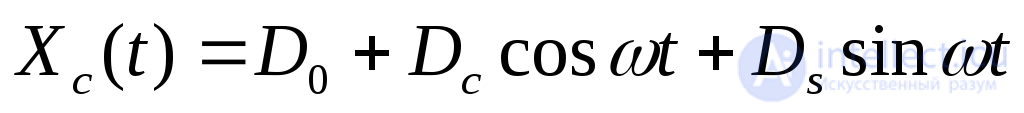(2.20)

где Do, D_c, D_s -одностолбцовые матрицы, которые определяются подстановкой (2.19) в (2.20). Об этом говорит сайт https://intellect.icu . Опуская промежуточные преобразования, запишем:

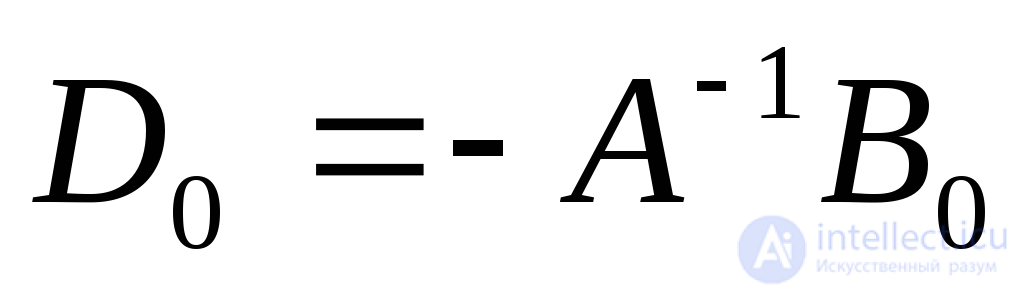
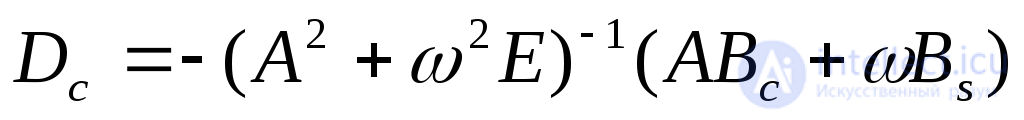(2.21)

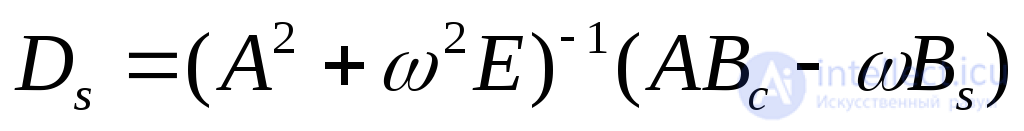
где Е -единичная матрица.

2. Непосредственный метод

Непосредственный метод поиска стационарных периодических решений систем линейных дифференциальных уравнений основан на возможности записать такое решение в явном виде:

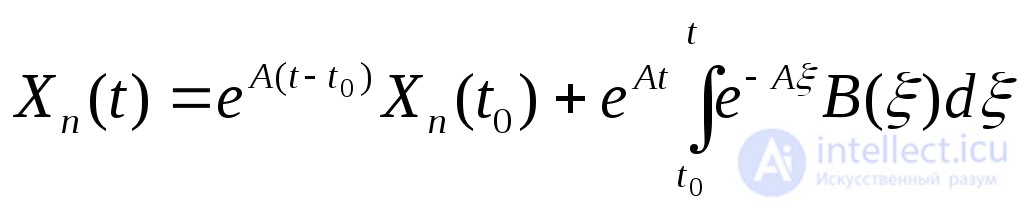
или 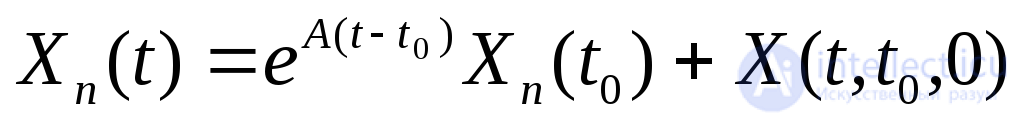, (2.22)

где 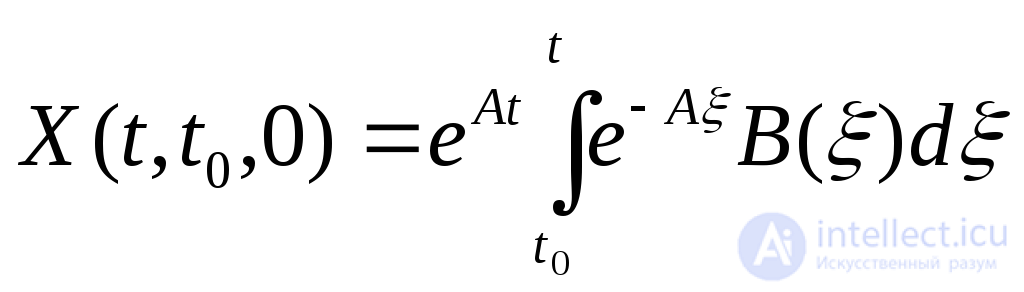- решение задачи Коши с нулевыми начальными условиями

Суть непосредственного метода сводится к определению вектора Xn(t₀)начальных условий для периодического решения. Используя условие периодичности

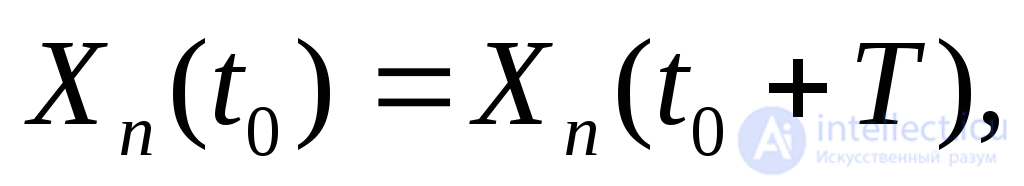
из (2.22) находим

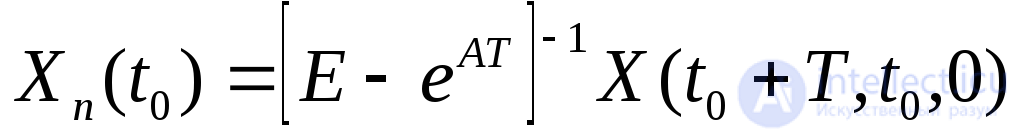(2.23)

Так как решение является периодическим с периодом Т,то начальный момент времениt₀ достаточно выбирать на интервале[0,Т],то есть 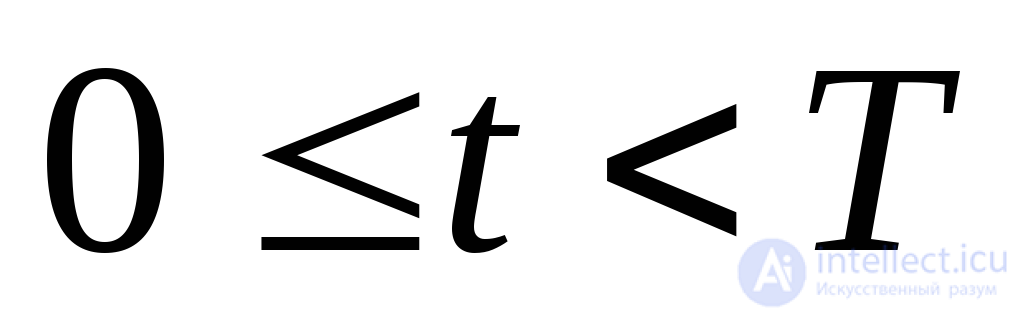.Без ущерба для общности будем выбирать начальный момент времениt₀ = 0,тогда выражение для начальных условий периодического решения (2.23) примет вид

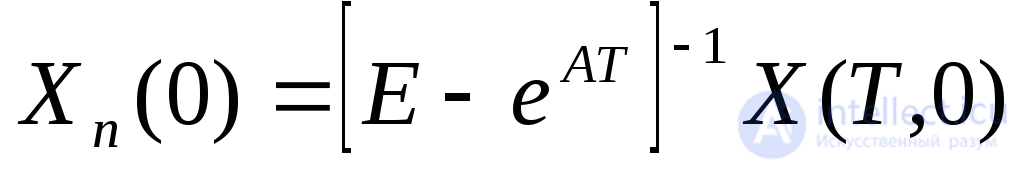(2.24)

где Х(Т,0) - решение задачи Коши с начальными условиямиХ(0) = О

Таким образом, для нахождения периодического решения непосредственным методом необходимо реализовать следующие этапы:

1. решить задачу Коши на одном периоде с нулевыми начальными условиями одним из численных методов; в результате определяется вектор Х(Т,0);

2. вычислить матричную экспоненту e^AT;

3. определить вектор начальных условий периодического решения Х_n(0)по формуле (2.24);

4. решить задачу Коши для исходной системы дифференциальных уравнений на одном периоде с начальными условиями Х(0)=Х_n(0).

На рис. 2.3 представлена блок-схема поиска вектора Х_n(0)начальных условий периодического решения непосредственным методом.

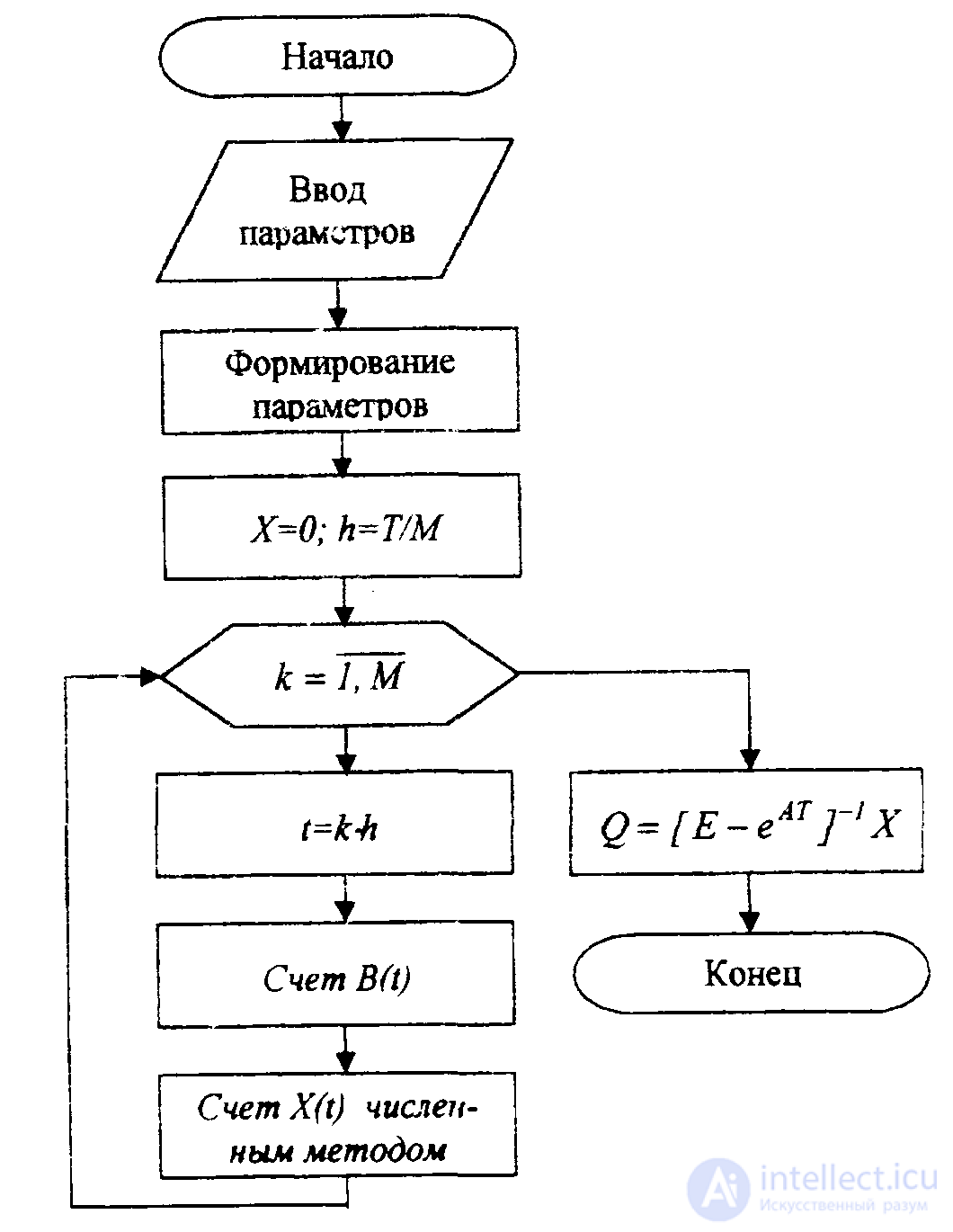
Рис 2.3

3. Метод установления

Полагая начальный момент времени t_n=0и учитывая условие периодичности, поиск периодического решения системы дифференциальных уравнений можно свести к решению системы трансцендентных уравнений относительно вектора начальных условийQ

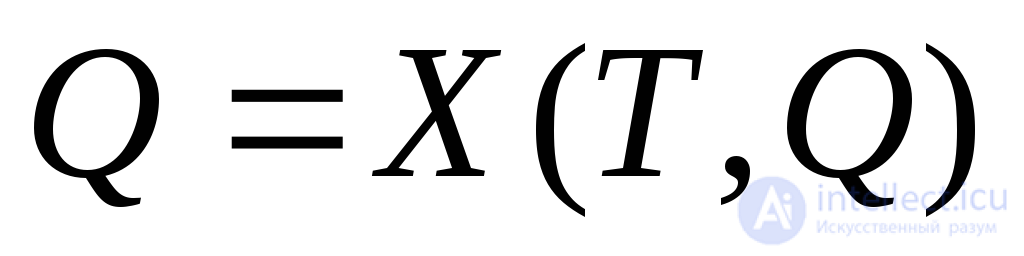(2.25)

Наиболее простой и естественный путь решения системы (2.25) - метод простой итерации:

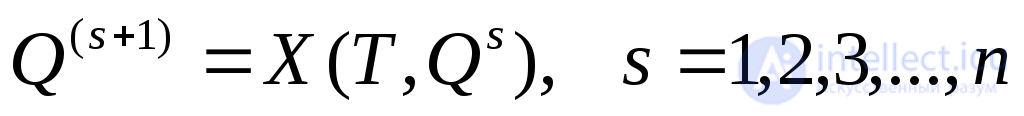(2.15) (2.26)

где вектор начального приближения Q⁽⁰⁾задается произвольным образом. Каждое последующее приближениеQ^(s+1)находится решением задачи Коши на интервале(О, Т)с начальным условием, задаваемым предыдущим приближениемQ^(s). Сдругой стороны, учитывая периодичность правой части системы дифференциальных уравнений,Q^(s+1)определяется решением задачи Коши на интервале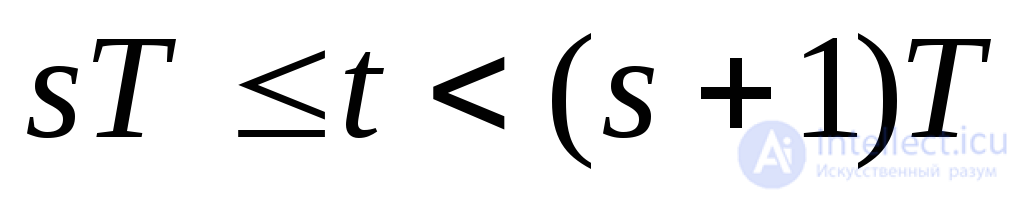 сусловиемX(sT)=Q^S,то есть реализация итерационного процесса (2.15) эквивалентна решению задачи Коши с начальным условием, задаваемым векторомQ⁽⁰⁾, на временном интервале, длительность которого определяется условиями сходимости. Поэтому метод поиска вектора начальных условий периодического решения по численной схеме (2.26) называют еще методом установления или поиском периодического решения через переходный процесс.

Выбор критерия окончания итерационного процесса (2.26) зависит от выбора нормы в пространстве векторов.

Если норма вектора определяется как 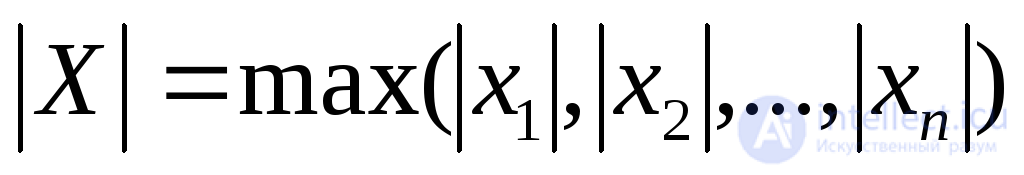, то в качестве критерия сходимости выбирают выполнение неравенства:

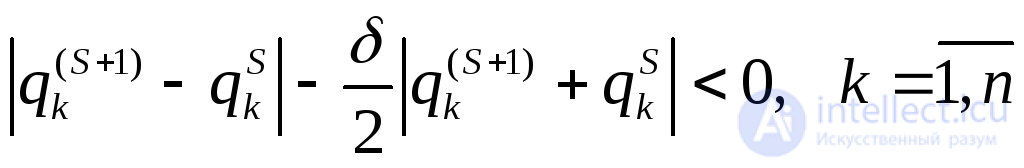(2.27)

Если в качестве нормы вектора принять, то критерием 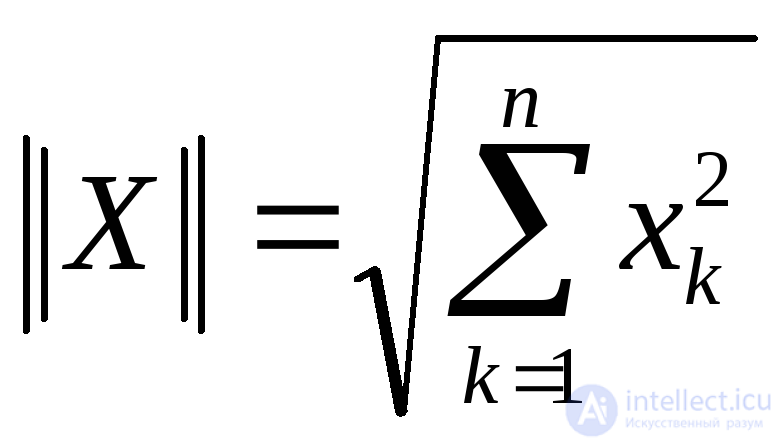окончания итерационного процесса будет служить неравенство:

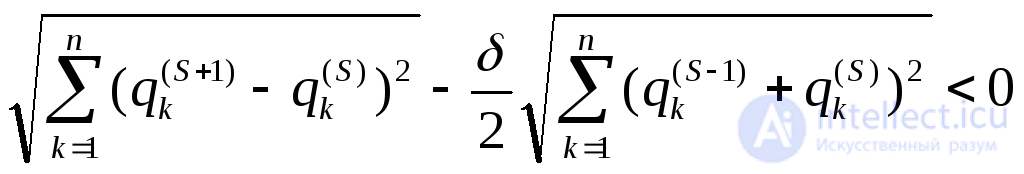(2.28)

В неравенствах (2.27) и (2.28) величина 8определяет относительную разницу между двумя соседними приближениями, то есть характеризует относительную точность вычисления вектора начальных условий периодического решения. Блок-схема алгоритма поиска периодического решения методом установления представлена на рис. 2.4.

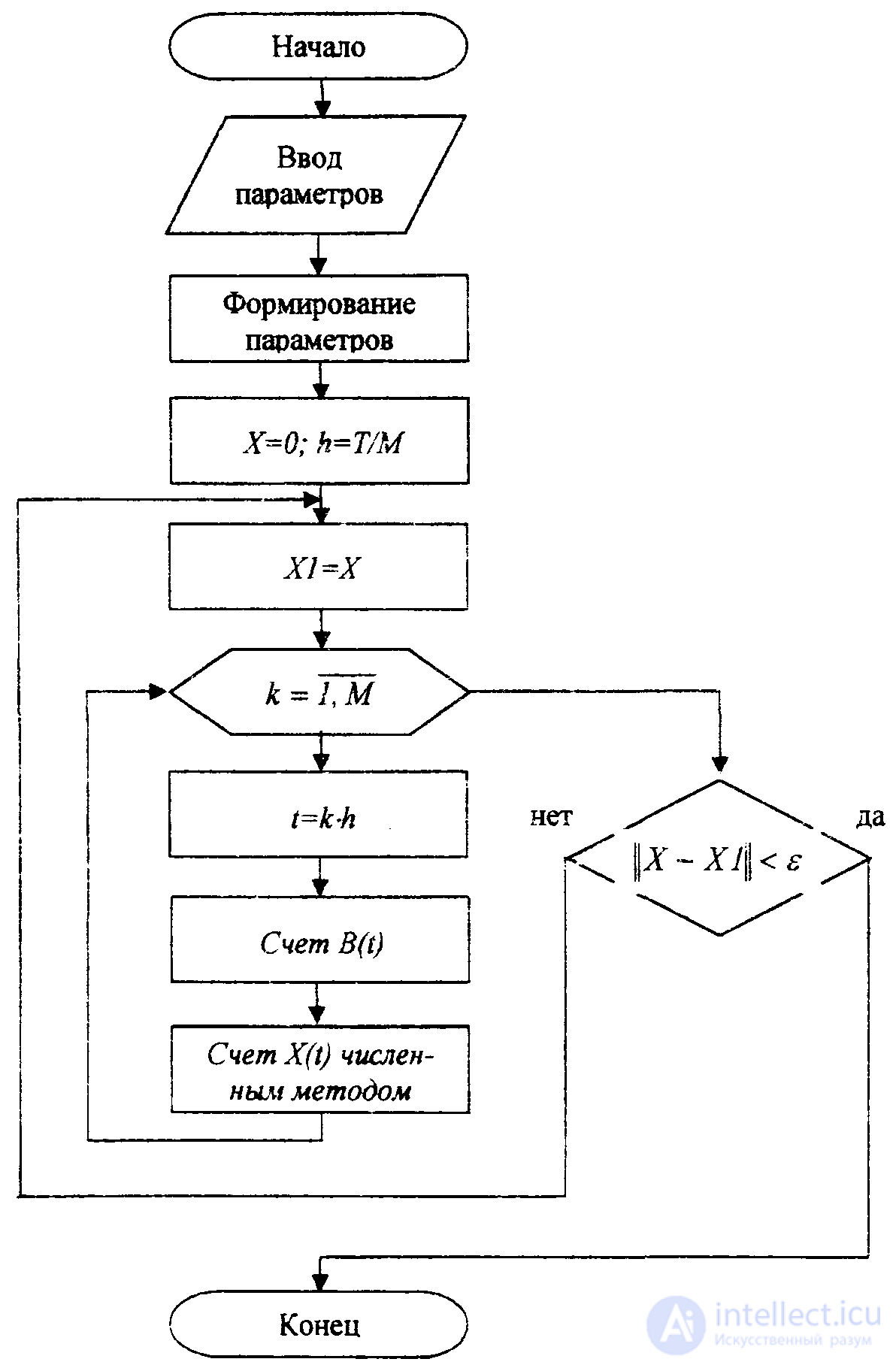
Рис 2.4

Вау!! 😲 Ты еще не читал? Это зря!

• моделирование
• дифференциальное уравнение
• задача Коши

Исследование, описанное в статье про методы поиска стационарных решений, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое методы поиска стационарных решений, стационарное решение, стационарный режим, стационарное движение, установившиеся движения и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем

Из статьи мы узнали кратко, но содержательно про методы поиска стационарных решений