Лекция
Привет, сегодня поговорим про понятие моделирования, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое понятие моделирования, моделирование, способы представления моделей, модели, виды моделей , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.
Модель — это аналог, прототип, шаблон, образец, используемый вместо оригинала для решения задач (получения ответов на вопросы). Модель строится на основании ограниченного множества известных нам данных (свойств, поведений) об оригинале. Построение моделей и использование моделей (решение на них задач) производится с целью:
модели рование – способ, процесс замещения оригинала его аналогом (моделью) с последующим изучением свойств и поведения оригинала на модели.
Процесс моделирования состоит из:
Модель вместо исходного объекта используется в случаях, когда эксперимент опасен, дорог, происходит в неудобном масштабе пространства и времени (долговременен, слишком кратковременен, протяжен…), невозможен, неповторим, ненагляден и т. д. Проиллюстрируем это:
Процесс моделирования есть процесс перехода из реальной области в виртуальную (модельную) посредством формализации, далее происходит изучение модели (собственно моделирование) и, наконец, интерпретация результатов как обратный переход из виртуальной области в реальную. Этот путь заменяет прямое исследование объекта в реальной области, то есть лобовое или интуитивное решение задачи. Итак, в самом простом случае технология моделирования подразумевает 3 этапа:формализация, собственно моделирование, интерпретация (рис. 1.1).
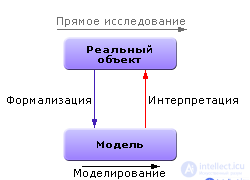
Рис. 1.1. Процесс моделирования (базовый вариант)
Если требуется уточнение, эти этапы повторяются вновь и вновь: формализация (проектирование), моделирование, интерпретация. Спираль! Вверх по кругу.
Более подробно весь цикл разработки показан на рис. 1.14, где отражены методы, способы, приемы, с помощью которых реализуется каждый из этапов.
Поскольку моделирование — способ замещения реального объекта его аналогом, то возникает вопрос: насколько аналог должен соответствовать исходному объекту?
Вариант 1: соответствие — 100%. Очевидно, что точность решения в этом случае максимальна, а ущерб от применения модели минимален. Но затраты на построение такой модели бесконечно велики, так как объект повторяется во всех своих деталях; фактически, создается точно такой же объект путем копирования его до атомов (что само по себе не имеет смысла).
Вариант 2: соответствие — 0%. Модель совсем не похожа на реальный объект. Очевидно, что точность решения минимальна, а ущерб от применения модели максимален, бесконечен. Но затраты на построение такой модели нулевые.
Конечно, варианты 1 и 2 — это крайности. На самом деле модель создается из соображений компромисса между затратами на ее построение и ущербом от неточности ее применения. Это точка между двумя бесконечностями. То есть, моделируя, следует иметь в виду, что исследователь (моделировщик) должен стремиться к оптимуму суммарных затрат, включающих ущерб от применения и затраты на изготовление модели (см. рис. 1.2).

Рис. 1.2. Соотношение суммарных затрат и точности для различных вариантов детализации прикладной модели
Просуммируйте две кривые затрат — получится одна кривая общих затрат. Найдите оптимум на суммарной кривой: он лежит между этими крайними вариантами. Видно, что неточные модели не нужны, но и абсолютная точность тоже не нужна, да и невозможна. Частое и распространенное заблуждение при построении моделей — требовать «как можно точнее».
«Модель — поиск конечного в бесконечном» — эта мысль принадлежит Д. И. Менделееву. Что отбрасывается, чтобы превратить бесконечное в конечное? В модель включаются только существенные аспекты, представляющие объект, и отбрасываются все остальные (бесконечное большинство). Существенный или несущественный аспект описания определяют согласно цели исследования. То есть каждая модель составляется с какой-то целью. Начиная моделирование, исследователь должен определить цель, отделив ее от всех возможных других целей, число которых, по-видимому, бесконечно.
К сожалению, указанная на рис. 1.2 кривая является умозрительной и реально до начала моделирования построена быть не может. Поэтому на практике действуют таким образом: двигаются по шкале точности слева направо, то есть от простых моделей («Модель 1», «Модель 2»…) ко все более сложным («Модель 3», «Модель 4»…). А процесс моделирования имеет циклический спиралевидный характер: если построенная модель не удовлетворяет требованиям точности, то ее детализируют, дорабатывают на следующем цикле (см. рис. 1.3).

Рис. 1.3. Спиралевидный характер процесса проектирования и уточнения прикладных моделей
Улучшая модель, следят, чтобы эффект от усложнения модели превышал связанные с этим затраты. Как только исследователь замечает, что затраты на уточнение модели превышают эффект от точности при применении модели, следует остановиться, поскольку точка оптимума достигнута. Такой подход всегда гарантирует окупаемость вложений.
Из всего сказанного следует, что моделей может быть несколько: приближенная, более точная, еще точнее и так далее. Модели как бы образуют ряд. Двигаясь от варианта к варианту, исследователь совершенствует модель. Для построения и совершенствования моделей необходима их преемственность, средства отслеживания версий и так далее, то есть моделирование требует инструмента и опирается на технологию
Инструмент — типовое средство, позволяющее достичь оригинальный результат и обеспечивающее сокращение затрат на выполнение промежуточных операций (имиджи, стандартные библиотеки, мастера, линейки, резинки…).
Технология — набор стандартных способов, приемов, методов, позволяющий достичь результата гарантированного качества с помощью указанных инструментов за заранее известное время при заданных затратах, но при соблюдении пользователем объявленных требований и порядка.
Среда — совокупность рабочего пространства и инструментов на нем, поддерживающая хранение и изменение, преемственность проектов и интерпретирующая свойства объектов и систем из них
Иногда модели пишут на языках программирования, но это долгий и дорогой процесс. Для моделирования можно использовать математические пакеты, но, как показывает опыт, в них обычно не хватает многих инженерных инструментов. Оптимальным является использование среды моделирования.
В нашем курсе в качестве такой среды выбрана «Система проектирования и моделирования Stratum-2000». Лабораторные работы и демонстрации, которые вы встретите в курсе, следует запускать как проекты среды Stratum-2000.
Модель, выполненная с учетом возможности ее модернизации, конечно, имеет недостатки, например, низкую скорость исполнения кода. Но есть и неоспоримые достоинства. Видна и сохранена структура модели, связи, элементы, подсистемы. Всегда можно вернуться назад и что-то переделать. Сохранен след в истории проектирования модели (но когда модель отлажена, имеет смысл убрать из проекта служебную информацию). В конце концов, модель, которая сдается заказчику, может быть оформлена в виде специализированного автоматизированного рабочего места (АРМа), написанного уже на языке программирования, внимание в котором уже, в основном, уделено интерфейсу, скоростным параметрам и другим потребительским свойствам, которые важны для заказчика. АРМ, безусловно, вещь дорогая, поэтому выпускается он только тогда, когда заказчик полностью оттестировал проект в среде моделирования, сделал все замечания и обязуется больше не менять своих требований.
Моделирование является инженерной наукой, технологией решения задач. Это замечание — очень важное. Так как технология есть способ достижения результата с известным заранее качеством и гарантированными затратами и сроками, то моделирование, как дисциплина:
Смежными моделированию предметами являются: программирование, математика, исследование операций.
Программирование — потому что часто модель реализуют на искусственном носителе (пластилин, вода, кирпичи, математические выражения…), а компьютер является одним из самых универсальных носителей информации и притом активным (имитирует пластилин, воду, кирпичи, считает математические выражения и т. д.). Программирование есть способ изложения алгоритма в языковой форме. Алгоритм — один из способов представления (отражения) мысли, процесса, явления в искусственной вычислительной среде, которой является компьютер (фон-Неймановской архитектуры). Специфика алгоритма состоит в отражении последовательности действий. Моделирование может использовать программирование, если моделируемый объект легко описать с точки зрения его поведения. Если легче описать свойства объекта, то использовать программирование затруднительно. Если моделирующая среда построена не на основе фон-Неймановской архитектуры, программирование практически бесполезно.
Какова разница между алгоритмом и моделью?
Алгоритм — это процесс решения задачи путем реализации последовательности шагов, тогда как модель — совокупность потенциальных свойств объекта. Если к модели поставить вопрос и добавить дополнительные условия в виде исходных данных (связь с другими объектами, начальные условия, ограничения), то она может быть разрешена исследователем относительно неизвестных. Процесс решения задачи может быть представлен алгоритмом (но известны и другие способы решения). Вообще примеры алгоритмов в природе неизвестны, они суть порождение человеческого мозга, разума, способного к установлению плана. Собственно алгоритм — это и есть план, развернутый в последовательность действий. Следует различать поведение объектов, связанное с естественными причинами, и промысел разума, управляющий ходом движения, предсказывающий результат на основе знания и выбирающий целесообразный вариант поведения.
Итак:
модель + вопрос + дополнительные условия = задача.
Математика — наука, предоставляющая возможность исчисления моделей, приводимых к стандартному (каноническому) виду. Наука о нахождении решений аналитических моделей (анализ) средствами формальных преобразований.
Исследование операций — дисциплина, реализующая способы исследования моделей с точки зрения нахождения наилучших управляющих воздействий на модели (синтез). По большей части имеет дело с аналитическими моделями. Помогает принимать решения, используя построенные модели.
Проектирование — процесс создания объекта и его модели; моделирование — способ оценки результата проектирования; моделирования без проектирования не существует.
Смежными дисциплинами для моделирования можно признать электротехнику, экономику, биологию, географию и другие в том смысле, что они используют методы моделирования для исследования собственного прикладного объекта (например, модель ландшафта, модель электрической цепи, модель денежных потоков и т. д.).
Рядом стоят дисциплины «Компьютерная графика» и «Модели и методы искусственного интеллекта» (см. рис. 1.4).

Рис. 1.4. Основные подсистемы при проектировании комплексных моделей
Компьютерная графика помогает организовать удобный естественный интерфейс для управления моделью, для наблюдения за ее реакциями. Важно понимать, что пользователь взаимодействует с моделью не напрямую, а именно через интерфейс: с одной стороны он посылает ей исходные (входные) данные (например, с помощью окон ввода, кнопок, движков, командной строки и т. д.), с другой — смотрит на результат работы модели, то есть воспринимает посредством интерфейса выходные данные.
Искусственный интеллект подразумевает построение высших моделей (например, адаптивных, которые умеют самонастраиваться, умеют создавать друг друга и т. д.). Подразумевается, что модель интеллекта в состоянии сама строить модели прикладных объектов и систем; объяснение того, как это делается, дается в курсе «Модели и методы искусственного интеллекта». Вместе с тем заметим, что ряд исследователей, говоря об искусственном интеллекте, имеют в виду применение моделей (обучения, воспроизведения, языка и т. д.) для изучения и имитации одной из самых сложных систем во Вселенной — человека.
Заметим, что искусственный интеллект — достаточно большая модель, которая содержит обширную информацию об окружающем мире и мета-модели, умеющие ее достраивать. Мета-модели имеют большое подобие с имитируемым ими человеком.
В зависимости от носителя различают модели: натурные, мысленные, математические, имитационные, графические, фотографические и так далее. Каждая из моделей обладает различной способностью к прогнозу свойств объекта. Например, по фотографии человека в анфас вряд ли можно верно представить, как выглядит его затылок. Приближение в виде трехмерной модели — намного лучше, но можно ли с ее помощью определить, когда, например, у виртуального человека вырастут волосы длиной 50 см? Имитационная модель еще более информативна. Но наибольшей ценностью обладают модели, пригодные для решения задач, то есть обладающие прогностическими свойствами, умеющие отвечать на вопросы. Следует различать два понятия — «модель» и «задача». Модель связывает переменные между собой законами. Эти законы действуют независимо от того, какая сейчас задача стоит перед нами. Модель объективна, она подобна миру, который нас окружает, и содержит в себе информацию об этом. Структура мира (в общем смысле) неизменна, фундаментальна, модель, следовательно, тоже. А человек, как существо субъективное, имеющее собственные цели, часто меняющиеся желания, ставит, в зависимости от своих потребностей, каждый раз новые задачи, требует решить возникающие у него проблемы. Он ставит вопросы к окружающему миру, с законами которого нельзя не считаться. Удобно ставить вопросы к модели, которая содержит нужную информацию о мире. Поэтому задача — это совокупность вопроса и модели. Можно к модели задавать все новые и новые вопросы и при этом не менять модель, но менять задачу.
То есть модель — способ нахождения ответов на вопросы. Чтобы ответить на поставленный вопрос, модель должна быть преобразована по правилам, обеспечивающим ее эквивалентность, к виду, соответствующему ответу на вопрос. Это означает, что модель должна быть сформирована по правилам определенной алгебры (алгебра есть правила преобразования). Об этом говорит сайт https://intellect.icu . А процедура, которая помогает применить такие правила к модели, называется методом.
Рассмотрим пример.
Модель падения тела под углом к горизонту содержит информацию о координатах траектории, заданных в осях (x, y): y = –x2 + 4 · x – 3 (координаты тела в полете) — см. рис. 1.5.

Рис. 1.5. Траектория движения тела, брошенного под углом к горизонту
Модель связывает две переменные y и x законом f(y, x) = 0. Модель может быть расширена некоторыми исходными данными, например, так: y = –x2 + 4 · x – 3, y = 0 (интересуют не все возможные значения y, а только точки на поверхности Земли).
y = 0 — это тоже закон, но более мелкого масштаба. Такие уравнения могут появляться и исчезать в зависимости от исследуемой проблемы. Обычно их называют гипотезами.
Вопрос: x = ?
Теперь модель и вопрос вместе образовали задачу:
y = –x2 + 4 · x – 3,
y = 0,
x = ?
Модель подразумевает, что исследователь может решать с ее помощью прямые и обратные задачи.Трактовать задачу можно так: при каких значениях x тело окажется на поверхности Земли?
Прямая задача не требует алгебраических преобразований, достаточно только арифметических подстановок: x = 2, y = –x2 + 4 · x – 3, y = ?. Ответ: y = 1. То есть, если на вход модели подать значение 2, то на выходе модели будет значение 1 — см. рис. 1.6.
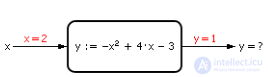
Рис. 1.6. Вид модели для решения прямой задачи
Обратная задача: y = 0, y = –x2 + 4 · x – 3, x = ? Ответ: x = 1, x = 3. То есть ответ говорит: чтобы на выходе модели обеспечить значение 0, надо, чтобы на вход модели было подано значение 1 (или 3).
И в первом, и во втором случае мы в разной мере преобразовывали модель, но всегда так, чтобы на входе у нее была известная величина, а на выходе — неизвестная.
В первом варианте y := –x2 + 4 · x – 3.
Во втором варианте модель преобразуется к виду: 0 = –x2 + 4 · x – 3. Здесь мы опустили ряд преобразований, известных из курса средней школы, а именно:
D := b2 – 4 · a · c, где a = –1, b = 4, c = –3.
x := (–b ± sqrt(D))/(2 · a).
x := 1 или x := 3.
Способность модели преобразовываться с помощью алгебры дает возможность в дальнейшем использовать ее многократно для решения различных задач, делать на ней прогнозы.Преобразования происходили с учетом правил алгебры. Если бы правила алгебры были нам неизвестны, то решить обратную задачу нам бы не удалось. А значит, не удалось бы ответить на поставленный вопрос: «x = ?».
Сравните: телефонный справочник — это тоже своеобразная модель, но какие прогнозы вы можете сделать, какие обратные задачи решить? Как вычислить фамилию абонента по номеру телефона? Какую алгебру вы используете?
Поэтому, создавая модель, следует обязательно думать о том, какой алгеброй она будет преобразовываться. Создавать алгебру следует параллельно с моделью или использовать уже готовую алгебру и не отходить при построении модели от ее правил.
Еще один тип задач, который приходится решать на моделях — задачи настройки модели.
Приведем пример. При каких значениях параметра a модель y = a · x2 + 4 · x – 3 обеспечит y = 9при x = 2? Решаем систему уравнений:
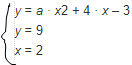
или
9 = a · 22 + 4 · 2 – 3
Далее, по правилам арифметики и алгебры, получим ответ: a = 1.
От показанного на рис. 1.7 структурного изображения модели можно перейти к другому, математическому, ее виду: Y = M(X).

Рис. 1.7. Структурное изображение модели в среде моделирования
Модель — закономерность, преобразующая входные значения в выходные. А как известно из математики, с выражением Y = M(X) можно решить три вида задач, которые приведены в табл. 1.1.
Таблица 1.1. Формы записи модели и типы решаемых задач
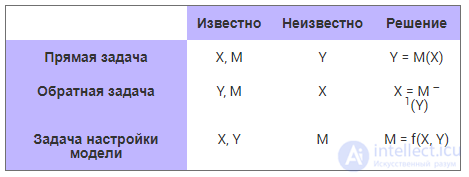
Ряд моделей может быть недоопределен — это означает, что вариантов ответов много (два, три, сто или бесконечное множество). Если нужен один ответ, то проблему надо доопределять, дополнять условиями. «Недоопределен» означает, что можно произвольно, кроме гипотез, законов, ответа, потребовать дополнительно выполнение еще каких-то условий. Возможно, при построении модели что-то не было учтено, не хватает каких-то законов. Рецепт понятен: модель надо достроить. Но может быть и по-другому. Решений много и есть, видимо, лучшие решения, и есть похуже. Тогда для нахождения лучшего решения следует сузить область решений, накладывая определенные ограничения, чтобы отсеять остальные. Такие задачи часто называют задачами управления.
Часть определений, которым надо безусловно удовлетворить, называются ограничениями.
Часть определений, относительно которых высказывают только пожелания («быть как можно больше или меньше»), называются критериями.
В целом получается обратная задача. А то, что надо определить — управляемая переменная. То есть интересуются: как следует изменить входной параметр (управление), чтобы обеспечить выполнение законов, не выйти за ограничения и чтобы при этом критерий принял наилучшее значение?
Пример. Модель: y = –x2 + 4 · x – 3. Вопрос: x = ? Доопределение модели: y должен быть максимизирован, x ≥ 2.5. Так как y должен быть максимизирован, то мы должны стараться двигаться вверх вдоль графика функции (рис. 1.8) и следить, чтобы значение x не стало меньше 2.5. Как видно из рисунка, значение y станет максимальным при x = 2.5. Ответ: y = 0.75, x = 2.5.
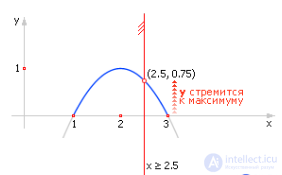
Рис. 1.8. Графическая иллюстрация решения задачи с ограничениями
Отметим, что создать модель бывает проще, чем сразу дать себе ответ на интересующий вопрос. Наверное, на практике вы замечали, что часто гораздо проще составить уравнения, чем угадать решение задачи. Например: решено разделить огромный шар размером с Землю на две половинки, полученную половинку снова поделить пополам и так далее. Попробуйте ответить на вопрос: сколько раз (n) надо провести такую операцию, чтобы размер делимой частички в результате достиг размера атома? Наверняка, сразу ответить на этот вопрос не удастся, интуиция подводит, придется составить модель.
Пусть D = 6 400 км = 6 400 000 м — диаметр шара (Земли), а d = 10–9 м — диаметр атома. Тогда модель есть выражение: 2n = D/d или 2n = 6 400 000/10–9. Отсюда получаем: 2n = 6.4 · 1015 илиn = log2(6.4 · 1015). Итак, приближенно, n = 53. Неожиданный результат, не правда ли?! Можно ли было его предугадать?
Еще несколько примеров. Тривиальные модели: x = 5°; телефон друга Сидорова — 912–36–54. Такие модели не несут в себе прогностических свойств, поскольку на основе известной информации невозможно вычислить каким-либо образом другую информацию. Зная телефон одного друга Сидорова, невозможно вычислить телефон другого его друга. Это так называемые пра-модели (pra-model). Фактически это данные.
Заметим, что недооценка в современных условиях понятия моделирования ведет к использованию в АРМах коммерческого назначения только данных. Именно поэтому такие АРМы не способны решать прогностические задачи и решают, в основном, только учетные задачи (см. рис. 1.9).
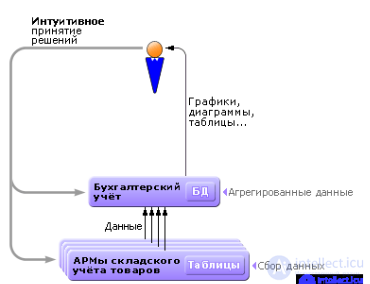
Рис. 1.9. Типовая схема взаимодействия АРМов в АСУ (без решения задач прогнозирования)
Чтобы проиграть ситуацию на предприятии на будущее, узнать, к чему приведет то или иное решение, следует в состав АРМов включать модели (см. рис. 1.10).
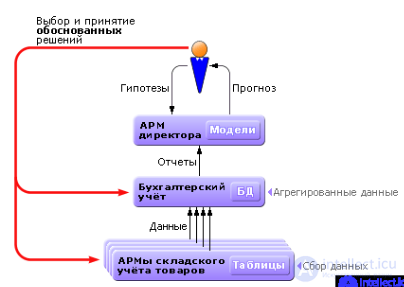
Рис. 1.10. Схема взаимодействия АРМов в АСУ (при постановке задач прогнозирования)
На рис. 1.11 показана пирамида моделей, различных по степени прогностичности.
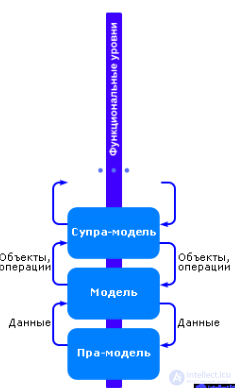
Рис. 1.11. Соотношение типов моделей по степени прогностичности
Обратите внимание: уровень «Модель» «питается» информацией, структурированной по типу предыдущего уровня «Пра-модель», то есть она потребляет на входе данные, перерабатывает их и возвращает тоже данные, то есть модели более низкого уровня (пра-модели). Подчеркнем еще раз, чтоданные — это тоже модели! Уровень «Супра-модель» потребляет на входе модели в виде объектов и операций, перерабатывает их и возвращает модели (примером таких супра-моделей могут служить грамматики, способные преобразовывать модели (уравнения). Более детально см. рис. 1.12). Данный принцип справедлив и для всех последующих (вышестоящих) уровней. Пирамида на рис. 1.11представлена в виде функциональных уровней; это означает, что каждый последующий уровень мощнее предыдущего, то есть он позволяет получить больший, более мощный качественный результат.
Модели могут принимать различную форму, в зависимости от способа мышления исследователя, его взгляда на мир, используемой алгебры. Использование различных математических аппаратов впоследствии приводит к различным возможностям в решении задач.
Модели могут быть:
Феноменологические модели сильно привязаны к конкретному явлению. Изменение ситуации часто приводит к тому, что моделью воспользоваться в новых условиях достаточно сложно. Это происходит оттого, что при составлении модели ее не удалось построить с точки зрения подобия внутреннему строению моделируемой системы. Феноменологическая модель передает внешнее подобие.
Абстрактная модель воспроизводит систему с точки зрения ее внутреннего устройства, копирует ее более точно. У нее больше возможностей, шире класс решаемых задач.
Активные модели взаимодействуют с пользователем; могут не только, как пассивные, выдавать ответы на вопросы пользователя, когда тот об этом попросит, но и сами активируют диалог, меняют его линию, имеют собственные цели. Все это происходит за счет того, что активные модели могут самоизменяться.
Статические модели описывают явления без развития. Динамические модели прослеживают поведение систем, поэтому используют в своей записи, например, дифференциальные уравнения, производные от времени.
Дискретные и непрерывные модели. Дискретные модели изменяют состояние переменных скачком, потому что не имеют детального описания связи причин и следствий, часть процесса скрыта от исследователя. Непрерывные модели более точны, содержат в себе информацию о деталях перехода.
Детерминированные и стохастические модели. Если следствие точно определено причиной, то модель представляет процесс детерминировано. Если из-за неизученности деталей не удается описать точно связь причин и следствий, а возможно только описание в целом, статистически (что часто и бывает для сложных систем), то модель строится с использованием понятия вероятности.
Распределенные, структурные, сосредоточенные модели. Если параметр, описывающий свойство объекта, в любых его точках имеет одинаковое значение (хотя может меняться во времени!), то это система с сосредоточенными параметрами. Если параметр принимает разные значения в разных точках объекта, то говорят, что он распределен, а модель, описывающая объект, — распределенная. Иногда модель копирует структуру объекта, но параметры объекта сосредоточенны, тогда модель — структурная.
Функциональные и объектные модели. Если описание идет с точки зрения поведения, то модель построена по функциональному признаку. Если описание каждого объекта отделено от описания другого объекта, если описываются свойства объекта, из которых вытекает его поведение, то модель является объектно-ориентированной.
Каждый подход имеет свои достоинства и недостатки. Разные математические аппараты имеют разные возможности (мощность) для решения задач, разные потребности в вычислительных ресурсах. Один и тот же объект может быть описан различными способами. Инженер должен грамотно применять то или иное представление, исходя из текущих условий и стоящей перед ним проблемы.
Приведенная выше классификация является идеальной. Модели сложных систем обычно имеют комплексный вид, используют в своем составе сразу несколько представлений. Если удается свести модель к одному типу, для которого уже сформулирована алгебра, то исследование модели, решение задач на ней существенно упрощается, становится типовым. Для этого модель должна быть различными способами (упрощением, переобозначением и другими) приведена к каноническому виду, то есть к виду, для которого уже сформулирована алгебра, ее методы. В зависимости от используемого типа модели (алгебраические, дифференциальные, графы и т. д.) на разных этапах ее исследования используются различные математические аппараты.
Полный (расширенный) вариант схемы, представленной на рис. 1.13, см. на рис. 1.14. После прочтения всего курса лекций рекомендуется вернуться к рис. 1.14 и детально, на более глубоком уровне, ознакомиться с ним.
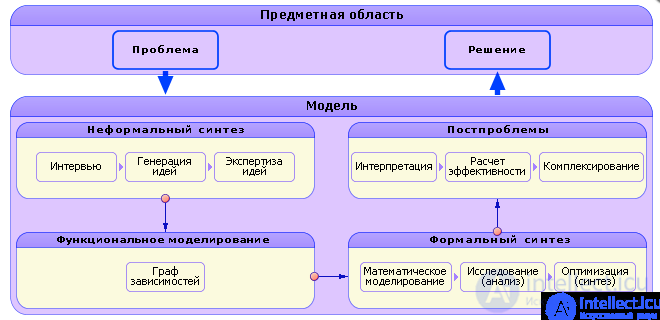
Рис. 1.13. Схема процесса моделирования (уточненный вариант)

продолжение следует...
Часть 1 Понятие моделирования. Способы представления моделей
Часть 2 Имитационный способ представления задачи 1 - Понятие моделирования. Способы представления
Надеюсь, эта статья об увлекательном мире понятие моделирования, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое понятие моделирования, моделирование, способы представления моделей, модели, виды моделей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем