Лекция
Это окончание невероятной информации про понятие моделирования.
...
alt="Понятие моделирования. Способы представления моделей" >
Рис. 1.15. Этапы процесса моделирования
Спираль, которая была рассмотрена на рис. 1.3, представлена на рис. 1.15 как виток. Но обратите внимание на возможность возвращения с каждого этапа на более ранний (или более ранние) при обнаружении ошибки. Спираль имеет достаточно сложный вид, прошита дополнительными связями.
Общее описание технологии моделирования расположено в файле справки системы «Stratum-2000» в разделе «Теория моделирования» («Помощь» > «Теория моделирования»). Сначала данный раздел стоит прочитать бегло, а затем подробно — после того, как вы усвоите весь курс и накопите опыт описания объектов на примерах и опыте, приобретенном в ходе выполнения курсовой работы.
Конечно, моделирование, как уже было сказано, в соединении с проектированием — это технология решения проблем, задач. Но у каждой технологии все-таки есть граница, за которой она менее эффективна. Такая граница есть и здесь. Посмотрите снова на рис. 1.13. Очевидно, что первые этапы решают менее формализованные задачи, а последующие — все более формальные. Соответственно, методы первых этапов менее формализованы, а последующих — более формальные, мощные. Это означает, что самые трудные и ответственные этапы для моделировщика — первые. Здесь от него требуется больше интуитивных решений. И ошибка на более ранних этапах больше сказывается на дальнейших решениях, возвращаться и переделывать приходится гораздо больше, чем на последних этапах. Поэтому удачные решения на первых этапах вызывают пристальный интерес системотехников, наука моделирования проявляет к ним повышенное внимание. Поскольку формальные методы легко автоматизируются, то последние этапы схемы поддержаны программными продуктами и легко доступны конечным пользователям, но наибольший интерес сегодня представляют программные продукты, поддерживающие первые этапы — системы, помогающие формализовать задачи. А также системы, обеспечивающие сквозное проектирование, доведенное до моделирования и конечной реализации (автоматическое порождение кода по описанию проекта).
Здесь можно упомянуть два направления. Первое — инструментальное. Проектировщику необходим инструмент для формального описания рассматриваемого им объекта. Известно несколько таких инструментов: RationalRose, «Аналитик», IDEF по технологии SADT, Stratum. Есть инструменты, подсказывающие решения, есть просто пассивные наборы, библиотеки. Одним из инструментов нахождения решений является технология АЛРИЗ; следуя ее алгоритму, отвечая на вопросы этой технологии, можно гарантированно придти к решению.
Второй путь — аналитические системы, выводящие из фактов знания. О них пойдет речь в следующем нашем курсе — «Модели и методы искусственного интеллекта».
В качестве примера посмотрим, как можно обнаружить, а потом описать закономерность.
Допустим, что нам нужно решить «Задачу о разрезаниях», то есть надо предсказать, сколько потребуется разрезов в виде прямых линий, чтобы разделить фигуру (рис. 1.16) на заданное число кусков (для примера достаточно, чтобы фигура была выпуклой).
Попробуем решить эту задачу вручную.
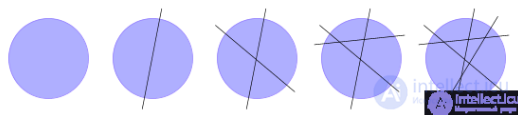
Рис. 1.16. Задача о разрезании фигуры на заданное число кусков
Из рис. 1.16 видно, что при 0 разрезах образуется 1 кусок, при 1 разрезе образуется 2 куска, при двух — 4, при трех — 7, при четырех — 11. Можете ли вы сейчас сказать наперед, сколько потребуется разрезов для образования, например, 821 куска? По-моему, нет! Почему вы затрудняетесь? — Вам неизвестна закономерность K = f(P), где K — количество кусков, P — количество разрезов. Как обнаружить закономерность?
Составим таблицу, связывающую известные нам числа кусков и разрезов.
Таблица 1.2. Таблица соответствия разрезов и получающихся фрагментов фигуры

Пока закономерность не ясна. Поэтому рассмотрим разности между отдельными экспериментами, посмотрим, чем отличается результат одного эксперимента от другого. Поняв разницу, мы найдем способ перехода от одного результата к другому, то есть закон, связывающий K иP.
Таблица 1.3. Таблица соответствия разрезов и получающихся фрагментов фигуры
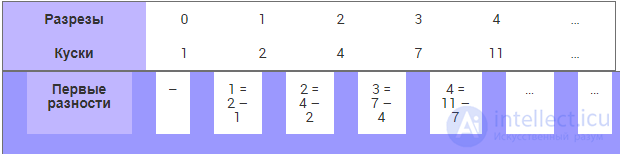
Уже кое-какая закономерность проявилась, не правда ли?
Вычислим вторые разности.
Таблица 1.4. Таблица соответствия разрезов и получающихся фрагментов фигуры
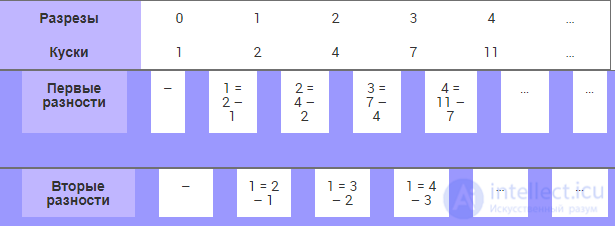
Очевидно, что далее продолжать процедуру вычисления разностей смысла нет.
Теперь все просто. Функция f называется производящей функцией. Если она линейна, то первые разности равны между собой. Если она квадратичная, то вторые разности равны между собой. И так далее.
Функция f есть частный случай формулы Ньютона:
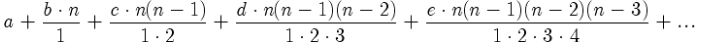
Коэффициенты a, b, c, d, e для нашей квадратичной функции f находятся в первых ячейках строк экспериментальной таблицы 1.5.
Таблица 1.5. Таблица соответствия разрезов и получающихся фрагментов фигуры
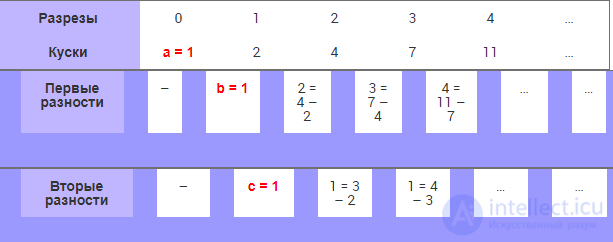
Итак, закономерность есть, и она такова:
K = a + b · p + c · p · (p – 1)/2 = 1 + p + p · (p – 1)/2 = 0.5 · p2 + 0.5 · p + 1.
Теперь, когда закономерность определена, можно решить обратную задачу и ответить на поставленный вопрос: сколько надо выполнить разрезов, чтобы получить 821 кусок? K = 821,K = 0.5 · p2 + 0.5 · p + 1, p = ?
Решаем квадратное уравнение 821 = 0.5 · p2 + 0.5 · p + 1, находим корни: p = 40.
Подведем итоги (обратите на это внимание!).
Сразу угадать решение мы не смогли. Поставить эксперимент оказалось затруднительно. Пришлось построить модель, то есть найти закономерность между переменными. Модель получилась в виде уравнения. Добавив к уравнению вопрос и уравнение, отражающее известное условие, образовали задачу. Поскольку задача оказалась типового вида (канонического), то ее удалось решить одним из известных методов. Поэтому задача оказалась решена.
И еще очень важно отметить, что модель отражает причинно-следственные связи. Между переменными построенной модели действительно есть крепкая связь. Изменение одной переменной влечет за собой изменение другой. Мы ранее сказали, что «модель играет системообразующую и смыслообразующую роль в научном познании, позволяет понять явление, структуру изучаемого объекта, установить связь причины и следствия между собой». Это означает, что модель позволяет определить причины явлений, характер взаимодействия ее составляющих. Модель связывает причины и следствия через законы, то есть переменные связываются между собой через уравнения или выражения.
Но!!! Сама математика не дает возможности выводить из результатов экспериментов какие-либо законы или модели, как это может показаться после рассмотренного только что примера. Математика это только способ изучения объекта, явления, и, причем, один из нескольких возможных способов мышления. Есть еще, например, религиозный способ или способ, которым пользуются художники, эмоционально-интуитивный, с помощью этих способов тоже познают мир, природу, людей, себя.
Итак, гипотезу о связи переменных А и В надо вносить самому исследователю, извне, сверх того. А как это делает человек? Посоветовать внести гипотезу легко, но как научить этому, объяснить это действо, а значит, опять-таки как его формализовать? Подробно мы покажем это в будущем курсе «Моделирование систем искусственного интеллекта».
А вот почему это надо делать извне, отдельно, дополнительно и сверх того, поясним сейчас. Носит это рассуждение имя Геделя, который доказал теорему о неполноте — нельзя доказать правильность некоторой теории (модели) в рамках этой же теории (модели). Посмотрите еще раз нарис. 1.12. Модель более высокого уровня преобразует эквивалентно модель более низкого уровня из одного вида в другой. Или генерирует модель более низкого уровня по эквивалентному опять же ее описанию. А вот саму себя она преобразовать не может. Модель строит модель. И эта пирамида моделей (теорий) бесконечна.
А пока, чтобы «не подорваться на ерунде», вам надо быть настороже и проверять все здравым смыслом. Приведем пример, старую известную шутку из фольклора физиков
«О вреде огурцов»
Огурцы вас погубят! Каждый съеденный огурец приближает вас к смерти. Удивительно, как думающие люди до сих пор не распознали смертоносности этого растительного продукта и даже прибегают к его названию для сравнения в положительном смысле («как огурчик!»). И, несмотря ни на что, производство консервированных огурцов растет.
С огурцами связаны все телесные недуги и вообще все людские несчастья.
Есть данные и о том, что вредное действие огурцов сказывается очень долго: среди людей, родившихся в 1889 году и питавшихся впоследствии огурцами, смертность равна 100%. Все лица рождения 1889—1909 годов имеют дряблую морщинистую кожу, потеряли почти все зубы, практически ослепли (если болезни, вызванные потреблением огурцов, не свели их уже давно в могилу).
Еще более убедительный результат, полученный известным коллективом ученых-медиков: морские свинки, которым принудительно скармливали по 20 фунтов огурцов в день в течение месяца, потеряли аппетит!
Единственный способ избежать вредного действия огурцов — изменить диету. Ешьте суп из болотных орхидей. От него, насколько нам известно, еще никто не умирал.
Движемся дальше. Сложность задачи часто диктует тот способ представления модели, который будет использоваться при ее описании. Покажем это на примере простейшей задачи.
Задача 1. Пусть два объекта (например, пешеход и велосипедист) движутся друг другу навстречу (рис. 1.17) со скоростями V1 и V2 соответственно. Необходимо узнать: когда и где встретятся эти объекты?
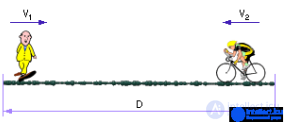
Рис. 1.17. Задача о встрече
Эта модель весьма далека от реальности. Что-либо изучить на ней представляется проблематичным, так как из нее можно найти только время T и место встречи S. Идеализация заключается в том, что дорога считается идеально прямой, без уклонов и подъемов, скорости объектов считаются постоянными, желания объектов не меняются, силы безграничны, отсутствуют помехи для движения, модель не зависит от величин D, V1, V2 (они могут быть сколь угодно большими или малыми).
T1 := D/(V1 + V2)
S1 := V1 · T1
Реальность обычно не имеет ничего общего с такой постановкой задачи. Но за счет большой идеализации (идеализации большого порядка) получается очень простая модель, которая может быть разрешена в общем виде (аналитически) математическими способами. Так формулируются чаще всего алгоритмические модели, где протянута цепочка вычислений от исходных данных к выходу. Поэтому мы применили в записи знак присваивания (:=). После вычисления правой части выражения ее значение присваивается переменной, стоящей в левой части. Далее значение этой переменной применено в правой части следующего выражения. Схематически это выглядит так, как показано нарис. 1.18.
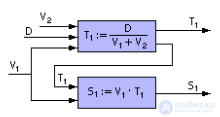
Рис. 1.18. Схема решения задачи о встрече (аналитический явный способ)
В данной формулировке за счет использования знака уравнивания получена связь переменныхf(T, V1, V2, D, S) = 0 в виде системы уравнений. Устанавливая знак «?» на различные переменные, можно формулировать при необходимости целый ряд произвольных задач, например так:
T1 · (V1 + V2) = D
S1 = V1 · T1
T1 = ?
При этом задачи формулируются пользователем и не предусматриваются специально моделировщиком. То есть модель имеет вид объекта. Мы получили более качественную модель. Идеализация ее велика, но за счет неявной формы записи появилась возможность изменения задачи, изучения на ней целого ряда проблем.
При имитационном способе решения обязательным является наличие некоего счетчика, который позволяет моделировать процесс по шагам или по деталям процесса.
Повторяя пошагово расчет в цикле, на каждом этапе работы алгоритма будем имитировать течение процесса (рис. 1.19). Обратите внимание, что процесс берется не в целом, а как бы в деталях, по шагам. Переменная t является координатой, а значит, отслеживается счетчиком с шагом h. Идея имитации — продвигать пешехода и велосипедиста на величину V · h на каждом такте, где h — достаточно малая величина. Поскольку мы рассматриваем множество актов движения по отдельности, можно по ходу менять все переменные модели, например, V. Если путь пройден большой (S1), то можно устроить привал (V = 0) на некоторое время. Остановка процесса имитации определяется суммой путей, пройденных велосипедистом и пешеходом навстречу друг другу, и сравнением ее с расстоянием D.
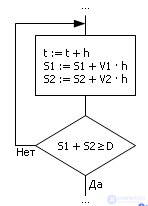
Рис. 1.19. Блок-схема решения задачи о встрече (имитационный алгоритмический способ)
На формально-математическом языке алгоритм выглядит так, как показано ниже.
t := t + h · e
S1 := S1 + V1 · h · e
S2 := S2 + V2 · h · e
e := ed(D – (S1 + S2))
f := not(e)
stop(f)
e — вспомогательный флаг;
f — флаг, показывающий, был ли пройден к текущему моменту t весь путь или нет;
ed(x) — единичная функция: ed(x) = 1 при x ≥ 0, иначе ed(x) = 0;
stop(z) — функция останова вычислений при z > 0.
Решение может быть найдено геометрически. Для этого в осях (t, S) схемой, показанной нарис. 1.20, строятся траектории движения объектов.
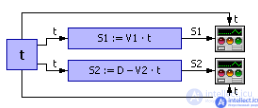
Рис. 1.20. Схема решения задачи о встрече (имитационный геометрический способ)
На рис. 1.21 вы видите картину, образованную двумя осциллограммами. Точка, в которой пересекаются осциллограммы, является предполагаемой точкой встречи двух объектов.
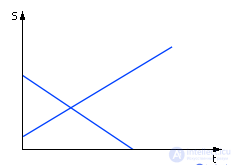
Рис. 1.21. Вид решения задачи о встрече (имитационный геометрический способ)
Главное отличие имитационных моделей от аналитических, которые мы рассмотрели выше, состоит в том, что имитационную модель можно постепенно усложнять, при этом результативность модели не падает.
Усложним задачу 1, введя в нее дополнительное условие. Представим, что на пути первого и/или второго объекта встретится помеха — пусть это будет участок железной дороги со шлагбаумом, который работает по случайному закону. Если шлагбаум открыт, то объект может переходить железную дорогу, в противном случае он не имеет права этого делать.
Промоделировать случайную работу шлагбаума можно с помощью генератора случайных чисел (ГСЧ). В различные моменты времени ГСЧ будет выдавать случайное число r = 0 или r = 1, это будет означать, что шлагбаум закрыт или, соответственно, открыт (см. рис. 1.22).
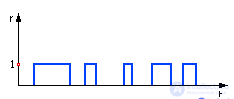
Рис. 1.22. Вид функции случайных помех (к задаче о встрече)
Частоту открывания шлагбаума можно контролировать, увеличивая или, наоборот, уменьшая число q, пересчитав случайное число r в z по формуле: z := ed(q – r).
На рис. 1.23 дана иллюстрация усложненной задачи 1.
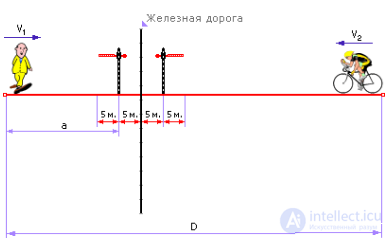
Рис. 1.23. Иллюстрация к усложненной задаче о встрече
На рис. 1.24 представлена алгоритмическая схема задачи.
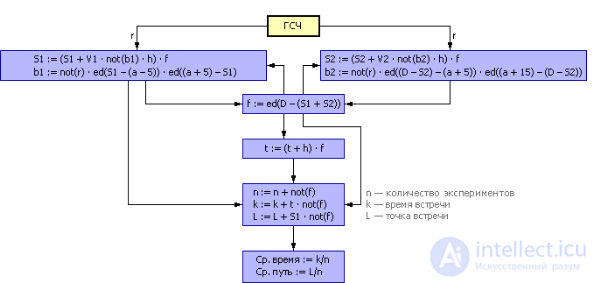
Рис. 1.24. Схема решения задачи о встрече (имитационный статистический способ)
Поскольку алгоритм использует случайные числа в качестве исходных данных, придется сделать несколько экспериментов и найти средние значения выходных величин. Результат одного эксперимента случаен и ни о чем не говорит. Среднее значение более информативно. Еще более информативны сведения о первом и втором моменте — среднем и разбросе значений вокруг него (дисперсии) и так далее.
Этот способ — еще один шаг к усложнению модели и приближению ее к реальным условиям. Если во всех предыдущих случаях скорость V была известна, то теперь она — непредсказуема, даже статистически, что чаще всего и наблюдается в реальных условиях. Скорость V объекта принимается из некоторых дополнительных моделей. Причем эти модели могут быть с обратными связями. Например, скорость может зависеть от обстановки, степени достижения цели, плана, целесообразности поведения, знания местности, желания двигаться (психологический мотив). Такая постановка ведет к адаптивным системам и системам искусственного интеллекта.
Например, если объект (пешеход) имеет возможность осмотреть местность с обзорной башни, то он может заранее просчитать свой путь и затем следовать ему. Без обзорной башни пешеход может зайти в безвыходный тупик или бесконечно долго перебирать варианты пути. Для адаптивных систем вводится критерий для оценки перспективности выбора направления движения.
Итак, подведем итог.
Модель — способ замещения реального объекта, используемый для его исследования, когда натуральный эксперимент невозможен, дорог, опасен, долговременен.
Примеры. Поскольку исследование Луны небезопасно для человека, для этой цели используют луноход как модель исследователя; поскольку реальные эксперименты над экономикой страны дороги по своим последствиям, то используют математические модели экономики для изучения последствий управляющих решений; поскольку процесс обработки металлов взрывом скоротечен во времени, то его изучают на модели в увеличенном масштабе времени, а процесс коррозии — в уменьшенном; атом изучается в увеличенном масштабе пространства, а космогонические процессы — в уменьшенном масштабе пространства; поскольку при проектировании объекта его попросту не существует, то исследование будущих свойств объекта ведется на модели.
Модель несет системообразующую и смыслообразующую роль в научном познании. На модели изучают неизвестные свойства предметов. Модель стремится как можно более ярко выразить структуру явления, его главные аспекты. Модель является концентрированным выражением сущности предмета или процесса, выделяя только его основные черты.
Знания — это модели окружающего мира, фиксируемые человеком в его мозгу или на технических носителях. Модели обладают повышенной наглядностью, выделяя главные аспекты сущности, и активно используются в процессах познания и обучения. Человек, решая, как ему поступить в той или иной ситуации, всегда пытается представить себе последствия решения, для этого он проигрывает ситуацию, представляет ее себе мысленно, строя модель в голове. Компьютер является усилителем для производства данной деятельности, инструментом информационной технологии. Компьютерные модели ускоряют процесс исследования, делают его более точным.
Алгоритмы — знания, выстраиваемые человеком (или, шире, разумным существом) в цепочку так, чтобы соединить исходное состояние с желаемым, целью; это один из вариантов ряда мероприятий, шагов, приводящих к цели.
Таким образом, модели — это основа разумной мыслительной деятельности; модели играют роль базиса, а моделирование — роль инструмента для прогнозирования.
Процесс моделирования состоит из трех стадий: формализации (переход от реального объекта к модели), моделирования (исследование и преобразования модели), интерпретации (перевод результатов моделирования в область реальности).
Модель есть зависимость F между входом X и выходом Y. Модель отражает закономерностьY = F(X). Часто модель является законом. Модель верна в рамках допущенных при ее построении гипотез. Поэтому модель ограничена некоторой областью и адекватна в ней.
Набор моделей образует научную дисциплину (механика, физика, горное дело и т. д.) Модель может быть расширена путем учета в ней дополнительных параметров. Тогда область ее применения становится шире.
Объект может быть представлен в виде аналитической или имитационной модели.
Аналитическое представление подходит лишь для очень простых и сильно идеализированных задач и объектов, которые, как правило, имеют мало общего с реальной (сложной) действительностью, но обладают высокой общностью. Аналитические модели обычно применяют для описания фундаментальных свойств объектов (поэтому ими так широко пользуется теоретическая физика), так как фундамент прост по своей сути. Сложные объекты редко удается описать аналитически.
Имитационное моделирование позволяет разлагать большую модель на части (объекты, «кусочки»), которыми можно оперировать по отдельности, создавая другие, более простые или, наоборот, более сложные модели. Таким образом, имитационное моделирование тяготеет к объектно-ориентированному представлению, которое естественным образом описывает объекты, их состояние, поведение, а также взаимодействие между ними. Имитационную модель можно постепенно усложнять и усложнять; аналитический способ этого не допускает или допускает, но с большими ограничениями.
Модель может быть соединена с другими моделями. Математически это означает совместное решение моделей (пересечение) и наложение тождеств на связываемые переменные. При связывании модели образуют систему, которая имеет определенную структуру (вложенную, параллельную, последовательную, смешанную, с обратными связями и т. д.)
Если к построенной модели добавить вопрос, то с помощью нее можно решить задачу, получить ответ, который заранее не очевиден. Если ответ заранее очевиден, то модель не строят. Обычно одна и та же модель годится для решения множества задач. Решая задачи, человек обычно строит модели в своей голове и оживляет (интерпретирует) их там же или на искусственном носителе (в среде моделирования).
Повторим:
модель + вопрос + дополнительные условия = задача.
В виде условий могут быть любые дополнительные выражения: равенства, присваивания начальных данных, неравенства, цели, функционалы и т. д., имеющие смысл ограничений, условий, дополнительных связей.
В виде вопроса может служить одна (или несколько) из неизвестных переменных.
Задача доопределяет свободные переменные модели, сужает область возможных решений.
Задачи, решаемые на модели, делятся на прямые и обратные. Прямые задачи по заданному Xнаходят Y путем подстановки X в уравнение Y = F(X). Обычно такие задачи называют задачами анализа. Обратные задачи по заданному Y находят X путем нахождения обратной функции F–1 и подстановки X = F–1(Y). Обычно их называют задачами синтеза. Если найти обратную функцию F–1 в явном виде затруднительно, то составляют вычислительные схемы для численного определения X. Часто к этому виду приводятся задачи управления объектами.
Еще одной специфической задачей является нахождение по заданным X и Y зависимости F или ее коэффициентов. Это задача построения (или настройки) модели.
Построив модель, исследователь может:
Поскольку модель является выражением конечного ряда и только важнейших для конкретного исследования аспектов сущности, то она не может быть абсолютно идентичной моделируемому объекту. Кроме этого, реальный объект бесконечен для познания. Поэтому нет смысла стремиться к бесконечной точности при построении модели. Для выяснения необходимой степени адекватности обычно строят ряд моделей, начиная с грубых, простых моделей и двигаясь ко все более сложным и точным. Как только затраты на построение очередной модели начинают превышать планируемую отдачу от модели, то уточнение модели прекращают. Первоначальные шаги производятся в каком-либо существующем универсальном моделирующем пакете. После одобрения модели под нее пишется специализированный пакет. Необходимость в этом возникает в случае, если функционирование модели в универсальной среде моделирования не удовлетворяет требованиям быстродействия (или каким-то другим).
В задачи данного курса входит изучение приемов и способов, необходимых для формализации, изучения и интерпретации систем.
Моделирование — прикладная инженерная наука класса технологических. Моделирование — дисциплина, ставящая целью построение моделей и их исследование посредством собственных универсальных методов, а также специфических методов смежных с ней наук (математика, исследование операций, программирование)
Надеюсь, эта статья об увлекательном мире понятие моделирования, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое понятие моделирования, моделирование, способы представления моделей, модели, виды моделей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем
Часть 1 Понятие моделирования. Способы представления моделей
Часть 2 Имитационный способ представления задачи 1 - Понятие моделирования. Способы представления
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем