Модель динамической системы в виде Фурье представления (модель сигнала)

Привет, сегодня поговорим про модель динамической системы в виде фурье представления модель сигнала , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое модель динамической системы в виде фурье представления модель сигнала , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.

Этот способ моделирования динамических систем основывается на том, что в любом сигнале присутствуют гармонические составляющие. В зависимости от частоты, составляющие называютсягармониками (первая, вторая и так далее). Сумма гармоник с соответствующими весами составляетмодель сигнала.

Пусть, например, в некотором сигнале присутствует сумма трех гармоник:3 · cos(t) + 2 · cos(3t) + 0.5 · cos(5t). Это значит, что в сигнале присутствует первая гармоника с амплитудой 3, третья гармоника с амплитудой 2, пятая гармоника с амплитудой 0.5. Сам суммарный сигнал выглядит так, как показано на рис. 7.1.

Рис. 7.1. Пример гармонического сигнала

Спектр этого сигнала показан на рис. 7.2. Ясно, что в нашем примере больший вес (амплитуду) в сигнале имеет (более других представлена) первая гармоника, наименьший вес имеет пятая гармоника.

Рис. 7.2. Пример спектра гармонического сигнала

Любой сигнал, сколь сложен бы он ни был, может быть представлен суммой гармоник. Более простой сигнал представляется меньшим числом гармоник, более сложный — большим. Быстро меняющийся сигнал, содержащий резкие пики, имеет в своем составе гармоники высоких порядков. Чем больше гармоник представлено в модели сигнала, тем точнее, в общем случае, модель отражает реальный сигнал.

Пусть задан некий сигнал X(t) (рис. 7.3).

Рис. 7.3. Временной сигнал на входе преобразования Фурье (возможный вид)

Определимся со временем рассмотрения сигнала: если сигнал периодический, то время рассмотрения равно периоду p сигнала; если сигнал непериодический, то периодом сигнала считается все время его рассмотрения.

…	…
…	…

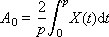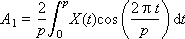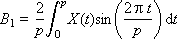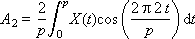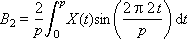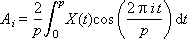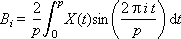A_i и B_i — это веса соответствующих гармоник, присутствующих в сигнале; i — номер гармоники. Об этом говорит сайт https://intellect.icu . Формулы их расчета называются прямым преобразованием Фурье.

Значение 2π · i/p = ω_i — это частота i-ой гармоники. Отметим также, что частота i-ой гармоники связана с частотой первой гармоники простым соотношением: ω_i = i · ω₁.

Отметим важную особенность данного способа представления: вместо всего сигнала во всех его подробностях достаточно хранить вектор чисел, представляющих весовые коэффициенты составляющих его гармоник: (A₀, A₁, A₂, …, B₁, B₂, …). То есть эти числа полностью характеризуют исходный сигнал, так как по ним сигнал можно полностью восстановить формулой обратного преобразования Фурье:

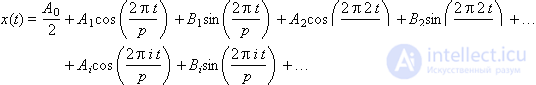
Именно эти числа используются также при обработке сигнала в модели динамической системы. Изображение этих чисел на графике в зависимости от номера гармоники (частоты) называетсяспектром сигнала (рис. 7.4). Спектр показывает, насколько присутствует в сигнале соответствующая составляющая. Спектр — это частотная характеристика сигнала.

Рис. 7.4. Сигнал, представленный в частотной области на выходе преобразования Фурье, спектр сигнала (возможный вид)

Здесь сигнал представлен в частотной области. Всегда по формулам прямого преобразования Фурье можно перейти из временной области в частотную, а по формулам обратного преобразования Фурье перейти из частотной области во временную. В какой области (частотной или временной) работать с сигналом в отдельный момент, решают из соображений удобства, наглядности и экономии вычислений. Заметим, что емкие с точки зрения вычислений операции интегрирования и дифференцирования сигнала во временной области заменяются на операции алгебраического сложения и умножения в частотной области, что с вычислительной точки зрения реализуется намного точнее и быстрее.

Система чисел A_i и B_i является полной характеристикой сигнала. Такой же полной характеристикой сигнала является система чисел S и φ, которые также образуют спектр (рис. 7.5). S — это амплитудно-частотная характеристика (АЧХ), φ — фазо-частотная характеристика (ФЧХ).

Рис. 7.5. Сигнал, представленный в частотной области, амплитудно-частотная и фазо-частотная характеристика сигнала (возможный вид)

Системы «A и B» и «S и φ» являются полностью равнозначными. Переход из системы «A и B» в систему «S и φ» производится по следующим формулам: S_i = sqrt(A_i² + B_i²) — абсолютная амплитуда сигнала; φ_i = arctg(B_i/A_i) — фаза сигнала, при сложении гармоник нужно учитывать сдвиг фаз (сдвиг фаз проиллюстрирован на рис. 7.8).

В случае с системой «S и φ» обратное преобразование Фурье имеет вид:

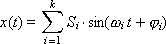
Рис. 7.6 и рис. 7.7 разъясняют смысл коэффициентов A и B разных гармоник. Эти коэффициенты — амплитуды синусов и косинусов соответствующих частот (гармоник). Во временной области графически они соответствуют размаху гармонических колебаний (рис. 7.6 и рис. 7.7); в частотной — высоте спектральной полоски на соответствующей частоте (рис. 7.4).

Рис. 7.6. Геометрическая иллюстрация параметров А и ω для косинусной составляющей гармонического сигнала

Рис. 7.7. Геометрическая иллюстрация параметров В и ω для синусной составляющей гармонического сигнала

Смысл чисел S_i и φ_i разъяснен на рис. 7.8.

Рис. 7.8. Геометрическая иллюстрация параметров S и φ для составляющей гармонического сигнала

Надеюсь, эта статья об увлекательном мире модель динамической системы в виде фурье представления модель сигнала , была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое модель динамической системы в виде фурье представления модель сигнала и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем