МЕТОДЫ МОДЕЛИРОВАНИЯ ТРАНСПОРТНОГО ПОТОКА

Привет, Вы узнаете о том , что такое моделирование транспортного потока, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое моделирование транспортного потока , настоятельно рекомендую прочитать все из категории Моделирование и Моделирование систем.

Основные принципы моделирования загрузки транспортных потоков

Транспортные потоки складываются из отдельных передвижений, совершаемых участниками движения, или пользователями транспортной сети. В общем случае, говоря о передвижениях, мы включаем в это понятие не только поездки различными
видами транспорта, но и пешие передвижения. Основными факторами, определяющими количество совершаемых передвижений и их распределение по транспортной
сети города, являются:

• • Потокообразующие факторы, т.е. размещение объектов, порождающих передвижения, таких как места проживания, места приложения труда, культурнобытового обслуживания и др.
• • Характеристики транспортной сети, такие как количество и качество улиц и дорог, параметры организации движения, маршруты и провозные способности общественного транспорта и др.
• • Поведенческие факторы, такие как мобильность населения, предпочтения при выборе способов и маршрутов передвижений и др.

можно моделировать и взаимодействовать между собой следующие типы трафика:

• Транспортные средства (легковые автомобили, автобусы и грузовики)
• Общественный транспорт (трамваи, автобусы)
• Велосипеды (велосипеды , мотоциклы )
• Пешеходы
• Рикши
• Людей и транспорт при эвакуации и поведении в толпе

Для построения математических моделей необходимо формальное описание указанных факторов. Основа такого описания — транспортный граф, узлы которого соответствуют перекресткам и станциям внеуличного транспорта, дуги — сегментам
улиц и линий внеуличного транспорта. В число дуг также включаются дуги, изображающие пересадки с уличного на внеуличный транспорт. Отдельной составляющей
транспортного графа является маршрутный граф общественного транспорта. Узлами маршрутного графа являются остановочные пункты, дугами — сегменты маршрутов между остановочными пунктами. С обычными узлами графа узлы-остановки
соединены дугами-посадками и дугами-высадками.
Для описания распределения потокообразующих объектов необходимо разделить
город на некоторое количество условных районов прибытия и отправления (ПО).
Каждый район ПО включается в граф как узел, соединенный с обычными узлами
графа специальными дугами-связями. Общий объем передвижений из одного района
ПО в другой (независимо от конкретных путей передвижения) называется межрайонной корреспонденцией.
Основой для моделирования поведения пользователей является математическая
формулировка критерия, на основании которого пользователь оценивает альтернативные пути и способы передвижения. Данный критерий принято называть обобщенной ценой пути. Увеличение обобщенной цены снижает привлекательность пути. Обобщенная цена пути складывается из обобщенных цен входящих в него дуг.
Кроме того, в цену пути может добавляться цена переходов с дуги на дугу, например
цена поворота при движении по улично-дорожной сети (УДС) или цена посадки при
переходе с дуги-пересадки на дугу, соответствующую поездке.
Пример эволюции транспортной сети и ее характеристик сети по модели Эрдеша-Реньи приведен на рисунке 3.

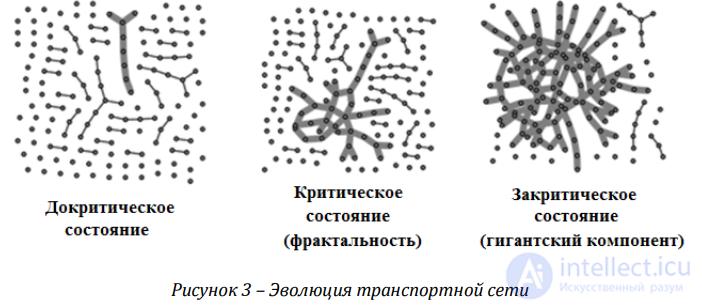
Рисунок 3 – Эволюция транспортной сети

Классификации моделей транспортного потока

Модели, применяемые для анализа транспортных сетей, весьма разнообразны. При этом на данный момент не существует исчерпывающей классификации методов моделирования. Систематизации в зависимости от решаемых задач осуществлялись по разным признакам. К примеру, в зависимости от метода решения – на аналитические и имитационные [2, 6]; по методам представления данных – на динамические модели, работающие в реальном времени, и статические, в которых параметры усредняются за определенный интервал времени [16]. По временной шкале различают непрерывные и дискретные модели [17]. По типу представления процесса модели делят на стохастические, в основе которых лежит зависимость от случайного сочетания параметров, и детерминированные, в которых следующее состояние транспортного потока однозначно определяется на основе предыдущего [15]. Основываясь на функциональной роли моделей, можно условно выделить три основных класса [16]: прогнозные модели, имитационные модели, оптимизационные модели. Подобная классификация не отражает метод решения, а также допущения, положенные в основу модели.

Наиболее популярной является классификация по уровню детализации транспортного потока [22], где выделяют макроскопические модели, мезоскопические модели, микроскопические модели, субмикроскопические модели. Однако такая классификация не дает представления ни об области применения, ни о методе моделирования.

На взгляд авторов настоящей работы, возможна следующая классификация моделей транспортного потока по двум основным признакам: уровню детализации и методу моделирования.

– Макроскопические:

• модели – аналоги (модель Лайтхилла и Уизема, модель Гриншилдса);

– Мезоскопические:

• модели расчета матрицы межрайонных корреспонденций (гравитационная, энтропийная модели);
• модели распределения потоков (модель равновесного распределения потоков и оптимальных стратегий);

– Микроскопические:

• модели следования за лидером (модель оптимальной скорости, «модель умного водителя»);
• клеточные автоматы.

Данная классификация учитывает как методы моделирования, так и степень детализации. Рассмотрим более подробно некоторые из вышеперечисленных моделей.

Рисунок 1– Модели моделирования транспортной сети

Макроскопические модели

Аналоговое моделирование описывает движение транспортных средств как движение специфической жидкости . В процессе моделирования изучаются усредненные характеристики потока, такие как плотность, средняя скорость, интенсивность, но отдельные транспортные средства не рассматриваются. Макроскопические модели могут быть непрерывными, описываемыми дифференциальными уравнениями в частных производных, или дискретными. Гидродинамические модели могут учитывать или не учитывать инерцию. Модели, не учитывающие инерцию, нередко получают из уравнения неразрывности и рассматривают скорость как функцию плотности. Данное обстоятельство позволяет описывать движение локально равновесного потока [14]. Модели, представленные уравнениями Навье – Стокса, учитывают эффект инерции и описывают тенденцию автомобилистов ехать с желаемой скоростью.

Рассмотрим распространенные примеры методов, наиболее точно отражающих основные характеристики макроскопического подхода [3, 11]. Модель Лайтхилла – Уизема – Ричардса (LWR) [19] относится к моделям-аналогам, основана на уравнениях гидродинамики и выполнении закона сохранения массы, под массой подразумевают количество автомобилей. Модель LWR не работает при очень низких и высоких плотностях транспортного потока, неадекватна вблизи «узких мест» и перекрестков со светофорами. Но, несмотря на это, гидродинамический подход стал основой для более совершенных моделей. Так, Пэйн [18] в 1971 г. предложил описать динамическую зависимость с помощью дифференциального уравнения конвекционного типа (уравнение было выведено из модели следования за лидером). Модель Пэйна следует понимать как закон сохранения, но из-за того, что скорость не зависит от плотности, вводится правая часть уравнения – сохранение импульса. Филипс учел внутреннее давление потока, которое заставляет водителей реагировать аналогично действиям лидирующего автомобиля [21]. Модель Гриншилдса (1934) содержит линейную зависимость плотности от скорости. Позднее она была модифицирована Ричардсоном. В модели Гриншилдса при определении пропускной способности важно правильно выбрать скорость свободного движения. В противном случае большое значение приведет к завышенным результатам, что подтверждается в работе [11]. Две последние модели имеют одну особенность: чем ниже скорость свободного движения, тем больше расчетные данные соответствуют экспериментальным. Логарифмический тип зависимости между плотностью потока и скоростью движения имеют макромодели Гринберга и Эл-Хозаини [17]. Модель Гринберга имеет серьезный недостаток: если плотность транспортного потока стремится к нулю, то значение скорости может стать больше, чем скорость свободного движения. Модель Эл-Хозаини работает адекватно, если задана высокая плотность потока, а его скорость не меньше 17 км/ч. Модели Андервуда, Дрейка и Зырянова имеют экспоненциальный тип зависимости между плотностью и скоростью автомобильного потока. Эти модели имеют один общий недостаток: если значение плотности движения будет достаточно большим, то полученная интенсивность превысит фактическую. Степенную зависимость между плотностью и скоростью имеют модели Д. Дрю и Л. Пайпса [17]. Особенность этих моделей заключается в том, что они могут быть приспособлены к экспериментальным данным благодаря коэффициенту пропорциональности.

В результате применения макроскопических моделей обычно определяются время движения, средняя скорость, уровень загрузки сети, интенсивность движения. Моделирование на макроуровне имеет определенные достоинства [12]: невысокие требования к ЭВМ, высокая скорость расчетов. Однако обладает и недостатками: полученные результаты являются статичными и недостаточно точными; для решения задач сложно определять исходные данные.

Мезоскопические модели

Мезомоделирование описывает автотранспортные средства (АТС) достаточно точно, но при этом рассматривает их взаимодействие и поведение так же, как на макроуровне [10, 16, 13]. Одной из первых моделей, отражающих взаимодействие пары районов, которые порождают транспортные потоки (корреспонденции), считается гравитационная модель. Основой для ее создания послужил закон всемирного тяготения. К ее недостаткам можно отнести то, что суммарное количество корреспонденций связывается только с одной парой районов. Однако посещения могут зависеть от расположения района прибытия среди других районов. Этот недостаток учтен в моделях семейства конкурирующих центров. Использование концепции энтропии для решения транспортных задач было предложено Вильсоном [4, 24]. В основе этой модели лежит второй закон термодинамики . Транспортная система схожа с физической тем, что в них имеется большое число неуправляемых элементов. Поэтому проблему определения корреспонденций предложено заменить максимизацией энтропии в транспортной системе [15].

В модели равновесного распределения предполагается, что все участники движения выбирают пути следования, исходя из минимальной цены поездки. В результате процесса «проб и ошибок» в системе устанавливается равновесное распределение потоков, обладающее свойствами, известными как требования Вардрупа [23]. Суть свойств заключается в следующем: при равновесном распределении автомобилей ни один участник движения не меняет свой путь, потому что цена поездки уже минимальна.

Основным достоинством перечисленных моделей является их сравнительная компактность. Однако эти модели имеют ряд недостатков: они охватывают лишь ограниченный набор параметров (скорость, задержки, очереди), слабо учитывают динамику транспортного потока.

Микроскопические модели

Базовая модель трафика, определяющая движение транспортных средств, была разработана Райнером Видеманном в 1974 году в Университете Карлсруэ . Об этом говорит сайт https://intellect.icu . Это модель для следования за автомобилем , которая учитывает физические и психологические аспекты водителей.

Модель, лежащая в основе динамики пешеходов, - это Модель социальной силы , разработанная Дирком Хелбингом и др. от 1995 г.

«Микроскопическое моделирование », иногда называемое микросимуляцией , означает, что каждый объект (автомобиль, поезд, человек) реальности моделируется индивидуально, т.е. соответствующей сущностью в моделировании, тем самым учитывая все соответствующие свойства. То же самое и для взаимодействий между сущностями. Противоположным ему было бы «макроскопическое моделирование», в котором описание реальности смещается с отдельных лиц на «усредненные» переменные, такие как поток и плотность . Называется соответствующий товар от того же производителя.Википедия site:tftwiki.ru

В этих моделях описывается движение каждой машины в отдельности. Микромодели стали популярными после появления мощных вычислительных компьютеров, потому что требовали большого объема расчетов. Такие модели хорошо подходят для представления движения по дороге с несколькими полосами, потому что могут описывать реалистичные правила перемещения автомобилей [5, 8, 15, 19]. Модель «следования за лидером» была одной из первых , разработали ее А. Решель (1950) и Л. Пайпс (1953). Основная идея заключена во влиянии головного автомобиля на следующие за ним машины. Влияние лидера косвенно выражено через зависимость оптимальной скорости от дистанции до впереди идущего автомобиля. С течением времени теорию разрабатывали и вносили изменения, в частности стали учитывать время реакции водителей, исследовали движение на многополосных дорогах, изучали устойчивость движения. В 1959 г. работники автоконцерна General Motors предложили для описания одной полосы движения свою микроскопическую модель, с помощью которой можно получить фундаментальную диаграмму. Следующим шагом стала модель Ньюелла [20], представленная в 1961 г. Основное предположение заключается в следующем: у каждого водителя есть своя «безопасная» скорость движения, которая зависит от расстояния до лидера. В этой модели важно правильно выбрать функцию зависимости скорости от интервала между машинами. Время реакции водителей стоит выбирать с осторожностью, при слишком больших значениях времени реакции появятся столкновения, а при малых могут возникнуть нереалистичные ускорения. Две последние рассмотренные модели можно объединить в одну общую микромодель «разумного водителя» . Она была предложена Трайбером в 1999 г. Движение в модели описывается как сочетание двух стратегий: ускорения и торможения. В зависимости от расстояния до впереди идущего автомобиля приоритет отдается одной из них. В модели умного водителя учитываются психофизические параметры людей, что помогает моделировать транспортные потоки более реалистично, случайно выбирая параметры автомобилистов.

Модели следования за лидером некорректно описывают динамику отдельного транспортного средства, что позволяет нам отнести их к мезоскопическим моделям. Также в моделях есть парадокс – если отсутствует лидер, то ускорение становится равным нулю.

Очень удобным аппаратом для реализации микроскопических моделей оказались клеточные автоматы . Предложил такую модель Дж. Фон Нейман в начале 1950-х г. . В моделях клеточных автоматов дорога разбивается на клетки, время считается дискретным. Каждая ячейка может находиться в каком-либо состоянии, которое определяется набором правил, зависящих от состояний соседних ячеек. Случайные возмущения вносят элемент стохастичности. Достоинством такого подхода является высокая эффективность при компьютерном моделировании. Недостатком же является относительно низкая точность в микроскопических масштабах, из-за дискретной природы клеточного автомата.

В результате работы микроскопических моделей, как правило, получают следующие данные: длина очереди, время задержки транспортных средств, средняя скорость, максимальная или минимальная скорость, время движения автомобилей. Основным достоинством микроскопических моделей является возможность получения оценок с высокой точностью. Однако высокая степень детализации в микромоделях влечет за собой следующие недостатки: требуется много ресурсов для сбора исходных данных; для получения достоверных результатов нужно большое число прогонов модели; необходима калибровка параметров; высокая чувствительность к ошибкам в исходных данных; сложности в получении аналитических зависимостей [15].

Математический аппарат моделирования трафика

Следует отметить, что для описания процессов в транспортных сетях могут быть применено множество подходов. Например, теория массового обслуживания [3-5], сети Петри [6,7], теория нечетких множеств [8,9], теория клеточных автоматов и многое другое. Несмотря на существующие разработки и конкретные решения в области управления, транспортные сети с точки зрения математического моделирования и управления являются очень сложными и плохо изученными объектами, требующими дальнейшего исследования На сегодняшний день, существует множество реализаций программных комплексов для моделирования транспортных потоков. Д

Как правило, во всех программах, моделирование транспортного потока происходит на микроуровне. Поэтому, начнем наш обзор именно с него. Рассмотрим самые распространенные модели.

Гравитационная модель.
Исторически одной из первых математических моделей, предложенных для оценки межрайонных корреспонденций, была гравитационная модель ]. Рассмотрим систему, состоящую из некоторого множества R районов
прибытия-отправления, соединенных между собой путями по транспортной сети. Исходными данными к расчету матрицы корреспонденций являются:
Oi — объем отправления из района i ∈ R,
Dj — объем прибытия в район j ∈ R.
В зависимости от типа корреспонденций объемы могут измеряться в автомобилях,
пассажирах или других удобных единицах. Предполагается выполненным условие
баланса общего прибытия и отправления

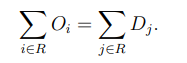
Если исходные данные не удовлетворяют этому условию, необходимо скорректировать данные умножением на постоянный коэффициент.
Гравитационная модель основана на следующем простом положении: корреспонденция из района i в район j пропорциональна общему объему отправления из центра i, общему объему прибытия в центр j и некоторой функции C(tij ), зависящей от
транспортного расстояния tij между центрами i и j. С интуитивной точки зрения
транспортное расстояние отражает степень близости районов с учетом скорости и
удобства передвижений, предоставляемых транспортной сетью. Способ определения
этой величины может различаться в разных вариантах модели.

При расчете однородной матрицы корреспонденций, т.е. корреспонденций, составленных из передвижений одного типа и пользователей одного класса, числовым выражением транспортного расстояния является обобщенная цена (в частном случае
время проезда) оптимального (кратчайшего) пути, соединяющего два района. Если
оцениваются смешанные корреспонденции, например включающие поездки как на
общественном, так и на легковом транспорте, необходимо вычислить оптимальную
цену передвижений на разных видах транспорта 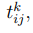, где k - типы передвижений. В
качестве транспортного расстояния тогда можно принять средневзвешенное этих цен
с учетом коэффициентов расщепления корреспонденции по типам передвижений:

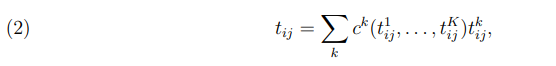
) - коэффициенты расщепления корреспонденции на типы передвижений как функции от набора оптимальных времен передвижений для разных типов;
эти коэффициенты удовлетворяют условию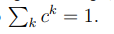
Обозначим через Fij корреспонденцию из района i в район j. Тогда гравитационная модель может быть сформулирована в виде

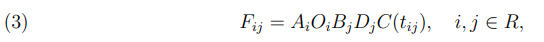
где коэффициенты определяются из условий

Функция C(t) называется функцией тяготения. Она является главным фактором, определяющим распределение передвижений по дальности, поэтому применяется также термин кривая расселения. В некоторых публикациях эта функция трактуется как «априорная вероятность зарождения корреспонденции» в зависимости
от расстояния, хотя в общем случае она не должна удовлетворять никаким условиям нормировки. Выбор этой функции осуществляется в ходе калибровки модели
на основе сопоставления выходного модельного распределения дальностей с данными обследований. Проведено большое количество исследований по калибровке этой
функции для разных городов . При практических расчетах часто
используется следующая аппроксимация:

Кинематическая модель использует в своей основе элементарное кинематическое уравнение, для того чтобы определить максимальную степень ускорения либо замедления, которое транспортное средство должно проявить, чтоб избежать столкновения с другим транспортным средством, движущемся впереди. В каждом временном отрезке (time-step) новое значение an+1должно быть достаточно высоким для того, чтоб избежать столкновения в выбранном часовом промежутке, который называется временем до столкновения – tc. Кроме того, необходимо постоянно изменять расстояние Dx, чтоб достичь определенного оптимального значения следующего отрезка dx. Скорость корректируется таким образом, чтобы оставаться в пределах [0 … Vmax].

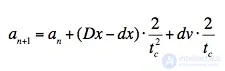
Так как модель опирается лишь на 2 параметра, усилия по ее калибровке будут достаточно невысокими. Но моделирование, очевидно, не достигнет высоких уровней правдоподобности также. Из-за ее ограничений, кинематическая модель имеет крайне малый вес в современном моделировании транспортных потоков и не рекомендована к применению с целью установления ширины проезжей части магистрали. Она включена в учебный процесс во многих ВУЗах Европы лишь с образовательной целью.

Энтропийная модель.
Использование концепции энтропии для решения транпортных задач было предложено Вильсоном , и затем данный подход развивался во многих работах . Энтропийная модель исходит из вероятностного описания поведения пользователей сети. Пользователи сети случайным образом распределяются
по некоторому набору возможных состояний. При расчете корреспонденций состоянием пользователя можно считать принадлежность его к корреспонденции из i в j.
Независимый и случайный выбор всеми пользователями своих состояний приводит к
тем или иным макроскопическим состояниям системы. Согласно основной концепции
энтропийной модели состояние системы, которое реализуется в реальности, есть состояние с наибольшим статистическим весом. Использование статистического веса
состояний вместо распределения вероятностей тех или иных состояний объясняется
тем, что в энтропийных моделях может не существовать конечного и нормированного распределения вероятностей. Статистические веса состояний отражают сравнительные вероятности реализации различных состояний в системе. С учетом этой
оговорки состояния с наибольшим статистическим весом часто также называются
наиболее вероятными состояниями.
Математически состояние с наибольшим статистическим весом определяется как
состояние, доставляющее максимум некоторой функции в пространстве состояний,
называемой энтропией системы. В применении к задаче определения корреспонденций в транспортной сети энтропия определяется следующим выражением:

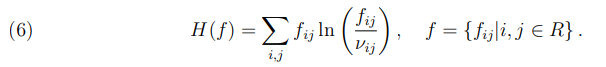
Здесь fij — числа заполнения состояний, т.е. количества элементов системы, находящихся в состояниях (i, j). Величины νij имеют смысл «априорных наиболее вероятных» значений fij . Фактические наиболее вероятные значения Fij определяются
из решения задачи о максимизации энтропии при некоторой системе ограничений
на fij . В отсутствие ограничений решение задачи максимизации приводит к априорным значениям Fij = νij . Ограничения, накладываемые на распределения, могут
быть самой разной природы. Как правило, эти ограничения отражают имеющуюся информацию о макроскопических характеристиках состояния системы. В системе
ограничений, применяемых в энтропийных моделях транспортных сетей, можно выделить группу стандартных линейных ограничений, выражающих баланс прибытий
и отправлений. Эта группа ограничений называется также транспортными ограничениями. С учетом сказанного энтропийная модель расчета корреспонденций может
быть записана в виде

Здесь явно выделены транспортные ограничения, а также включены в общем виде N
дополнительных ограничений-равенств и M ограничений-неравенств. Задача оптимизации (7)-(8) является стандартной задачей математического программирования
с выпуклой целевой функцией. Система ограничений в этой задаче, как правило,
линейна. Решение задачи в общем случае может быть получено методом множителей Лагранжа. В частном случае, когда имеются только транспортные ограничения,
можно получить аналитическое выражение для решения задачи (7)-(8). Это выражение совпадает с выражением, даваемым гравитационной моделью, если задать
априорные вероятности в соответствии с функцией тяготения: νij = C(tij ). Другой
способ установить связь между энтропийной и гравитационной моделью предложен
в [112]. Предположим, что передвижения между районами прибытия и отправления
i и j связаны с некоторым количеством «обобщенных затрат». Пусть для каждого
района отправления известны суммарные общие затраты на передвижения:

Данные равенства могут быть использованы в качестве ограничений в задаче максимизации энтропии. Они называются затратными ограничениями. Рассмотрим энтропийную задачу, в которой априорные вероятности тех или иных значений корреспонденций равны: νij = const, а в число ограничений включены балансовые и
затратные ограничения. Решение задачи также будет совпадать по виду с выражением гравитационной модели, если принять tij = cij и взять функцию тяготения
вида

Коэффициент λ в этом выражении есть множитель Лагранжа задачи оптимизации,
его значение определяется в ходе решения самой задачи. Согласно такой аргументации энтропийная модель может служить статистическим обоснованием для гравитационной модели, причем дает основание для выбора функции тяготения.
В рамках задачи максимизации энтропии может быть также осуществлен расчет корреспонденций с одновременным расщеплением по типам передвижений. Согласно общему подходу будем считать, что случайное состояние пользователя транспортной сети заключается в принадлежности к корреспонденции из i в j и выборе способа передвижения k. Состояние системы тогда определяется трехиндексным набором

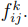. Выражения для энтропийной функции и соответствующей задачи максимизации вполне аналогичны (6)-(8). При этом в состав ограничений должны быть включены дополнительные ограничения по общему объему передвижений для разных типов .

Вероятностная модель BANDO. В 1995 году Бандо и его коллеги презентовали так называемую «оптимальную скоростную модель» (Optimal Velocity Model). Она представляет собой скоростную модель плотности, которая относится к группе детерминированных ведущих моделей и связывает целевую скорость транспортных средств с макроскопической плотностью транспортного потока. Бандо вывел оптимальную скорость таким образом, чтобы каждое транспортное средство старалось следовать следующему отношению:

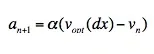
где:

an+1– ускорение для следующего отрезка времени;

α – фактор чувствительности (значение, обратное времени реакции

водителя);

vopt – оптимальная скоростная функция;

dx – изменение расстояния к предыдущему автомобилю;

vn – текущая скорость транспортного средства.

Команда Бандо предложила оптимальную скоростную функцию, которая монотонно увеличивается, с верхней границей в vmax.

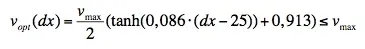
Со временем, модель была модифицирована еще несколькими оптимальными скоростными функциями. Например, используя разные функции ускорения или дифференцируя между свободной скоростью транспортного средства (ненасыщенный транспортный поток) и скоростью на пределе пропускной способности (speed-at-capacity) (насыщенный транспортный поток) с уравнением с 4-мя параметрами (Van Aerde, 1995).

Вероятностная модель GAZIS. Так называемая теория следования за автомобилем («гонка за лидером»), основана на исследованиях Gazis, Herman і Rothery (1961), старается следовать поведению транспортного средства, детерминируя расстояние, рассматривая время реакции водителя к определенным стимулам (например, разные скорости впередиидущего автомобиля), согласно формулы:

где:

an+1 – ускорение после времени реакции tp;

α0 – фактор чувствительности;

m, l – параметры калибровки (коэффициенты);

dx – разница скорости с предыдущим транспортным средством.

Для немецких магистралей значения параметров m і l были установлены в исследованиях Hoefs (1972) для различных сценариев (отдаление или приближение автомобиля спереди, с тормозными сигналами или без них). Однако, из-за стабильного увеличения автомобилей на европейских магистралях, в ходе развития пакета моделирования BABSIM была выполнена перекалибровка эталонных параметров, что привело к получению новых наборов параметров и более реалистичным результатам моделирования.

Вероятностная модель смены полосы движения Sparmann. Опираясь на работы Вайдемана, Спарман развивал алгоритм изменения полосы движения для двухполосного шоссе (Sparmann, 1978). Принимая во внимание все шесть потенциальных партнеров для взаимодействия (то есть каждое транспортное средство спереди, сзади на текущей полосе, а так же на двух соседних), транспортное средство могло бы изменить полосу движения, используя параметры Вайдеманна. Как только появилась потребность в изменении полосы движения, осуществляется проверка – подвергнет ли такой переход опасности или его или его так называемого “партнера взаимодействия”. Если обеспечивается безопасность всех транспортных средств, начинается процесс перестроения и транспортное средство оказывается на соседней полосе. Одно неудобство модели Спармана – нехватка более упреждающего стратегического подхода. Рассматриваются только соседствующие транспортные средства, игнорируя потребность других транспортных средств сменить полосу движения.

Вероятностная модель смены полосы движения THEIS. Тейс (1997) добавил стратегический компонент к модели Спармана: если транспортное средство пытается перестроиться на определенную полосу, оно должно для начала “просить” помощь у соседних транспортных средств. И наоборот, участвующее во взаимодействии транспортное средство должно решить, ускориться ли или замедлиться, чтобы создать интервал для меняющего полосу транспортного средства, или самому сменить полосу, чтобы создать ему место.

Модель WIEDEMANNа в составе программного комплекса PTV Vision VISSIM. Имитационное моделирование. Система имитации VISSIM состоит из двух отдельных программ, которые взаимодействуют друг с другом с помощью интерфейса, в котором происходит обмен данными измерений детекторов и данными о состояниях систем регулирования. Результат имитации – это анимация движения транспорта в виде графики в режиме реального времени и последующая выдача всевозможных транспортно-технических параметров, таких как, например, распределение времени в пути и времени ожидания, дифференцированных по группам пользователей.

В модель транспортного потока заложены модель следования за впереди идущим транспортным средством (ТС) с целью отображения движения в колонне за впереди идущим ТС по одной полосе движения и модель смены полосы движения. Зависящая от транспортного движения логика регулирования моделируется с помощью внешних программ регулирования светосигнальных установок. Программа для логического управления запрашивает параметры детекторов в такте от 1 секунды до 1/10 секунды (в зависимости от настройки и типа светофорных установок). Из полученных значений и временных интервалов программа определяет состояние всех систем регулирования для следующего шага имитации и вносят их в имитацию транспортного потока.

Существенным для точности системы имитации является качество модели потока транспортного движения, т.е. метода, с помощью которого рассчитывается передвижение транспортных средств в сети. В отличие от более простых моделей, в которых за основу берутся постоянные скорости и неизменное поведение следования за впереди идущими транспортными средствами, PTV Vision® VISSIM использует психофизиологическую модель восприятия Вайдеманна (1974 г., 1999 г.). Основная идея модели заключается в том, что водитель транспортного средства, движущегося с более высокой скоростью, начинает тормозить при достижении своего индивидуального порога восприятия относительно удаленности от впереди идущего транспортного средства, когда дистанция до впереди идущего транспортного средства начинает восприниматься им как слишком маленькая. Так как он не может точно оценить скорость впереди идущего транспортного средства, то его скорость будет падать ниже скорости впереди идущего транспортного средства до тех пор, пока он не начнет снова немного ускоряться после достижения своего порога восприятия, когда он начнет воспринимать возникшую между ним и впереди идущим ТС дистанцию как слишком большую. Это ведет к постоянному легкому ускорению и замедлению. С помощью функций распределения для скорости и дистанции имитируется различное поведение водителей.

Имитационные модели этого типа относятся к семейству car- following:

• • Gazis-Herman-Rothery(GHR)
• • CollisionAvoidancemodel(CA)– Модели Kametani и Sasaki, Гиппс, Лѐйцбаха, Крауса
• • PsychophysicalorActionPointmodel(AP) – Модель Видеманна
• • Linearmodel– Модели Helly, Hanken и Rockwell, Burnham и Seo, Aron Xing
• • Fuzzylogic-basedmodel28.06.2010 – Модели Rekersbring, Henn, McDonald и Wu.

Модели семейства car-following ориентируются на характеристики индивидуального транспортного средства. Модель Вайдеманна класса PSM выигрывает по количеству учитываемых факторов в моделировании транспортного трафика на микроуровне. Модель Вайдеманна включает в себя характеристики водителя, самого транспортного средства и представляет золотую середину между клеточными автоматами и остальными классами моделей семейства car-following.

После многочисленных эмпирических исследований, проведенных техническим университетом города Карлсруэ, эта модель следования за впереди идущим ТС стала эталонной. Более актуальные измерения доказывают, что изменившаяся за последние годы манера езды и технические возможности транспортных средств корректно отображаются в данной модели.

На многополосных проезжих частях водитель в VISSIM-модели учитывает не только впереди идущие транспортные средства, но и транспортные средства на обеих соседних полосах. Особенное внимание у водителя дополнительно вызывает светофор в 100 м перед достижением стоп – линии.

В VISSIM так называемые единицы водитель – транспортное средство двигаются по сети. Каждый водитель со своими индивидуальными параметрами поведения соотносится с определенным транспортным средством. При этом манера езды совпадает с техническими возможностями транспортного средства.

Имитационное моделирование, на данном этапе представляется мощным инструментом для оценки и анализа движения транспортных и пешеходных потоков. Кроме того, программа уровня PTV Vision® VISSIM позволяет в значительной мере упростить работу проектировщика и создает достоверную платформу для проектирования как дорожно-транспортных, так и любых градостроительных объектов.

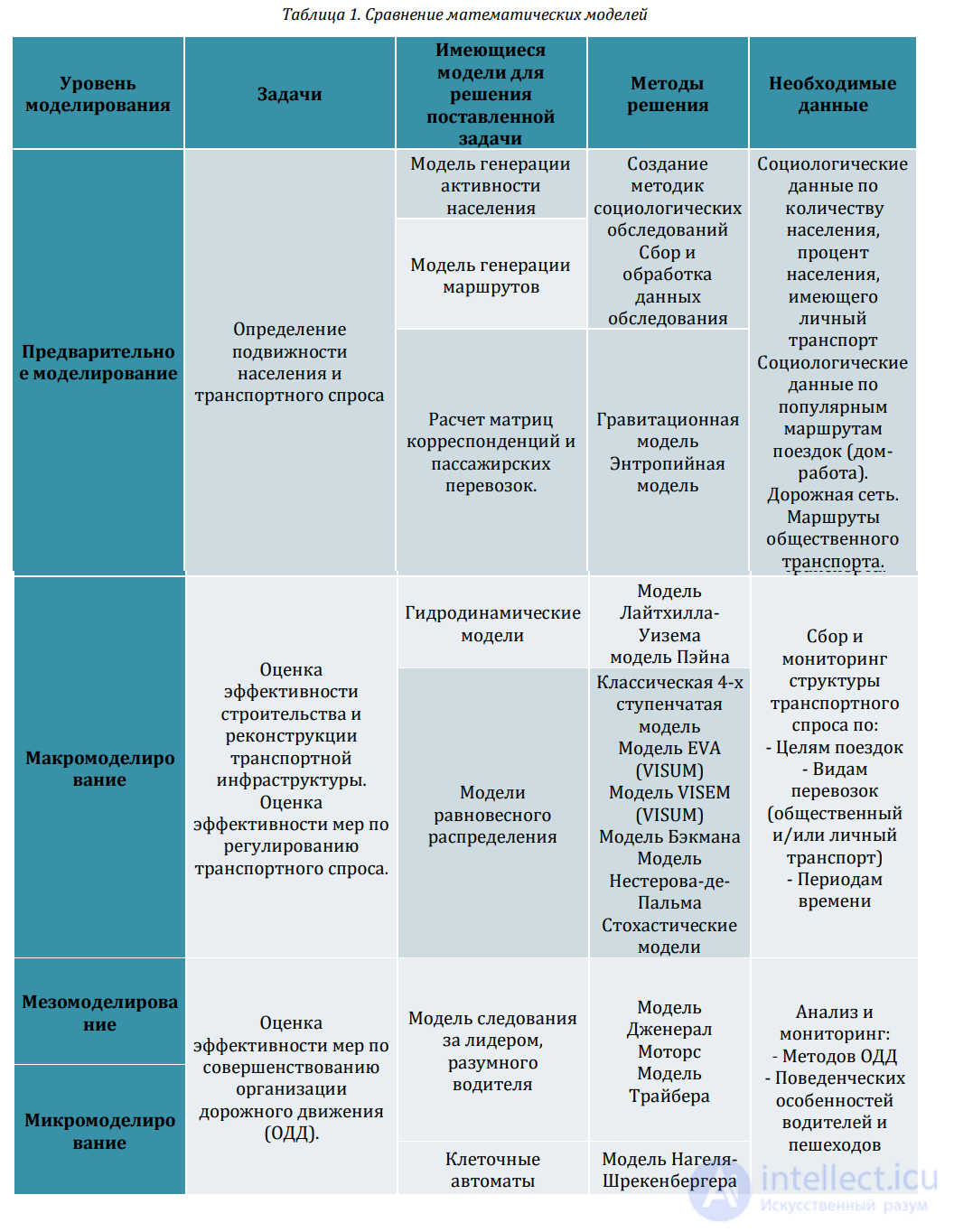
Таблица 1. Сравнение математических моделей

Исследование, описанное в статье про моделирование транспортного потока, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое моделирование транспортного потока и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Моделирование и Моделирование систем