Рис. 7. Схема образования тора
Поведение системы характеризуется следующими параметрами:
• особь может переместиться на любую клетку, имеющую с данной общую
сторону. Направление выбирается случайно из возможных свободных.
• особь может оставить потомство в той клетке, из которой она переместилась.
Потомство появляется периодически, период является параметром.
• если особь является «хищной», то она может поглотить свою жертву, при этом
перемещаясь на место жертвы.
• особь живет ограниченное количество времени, называемое временем жизни
особи – так же параметр.
• если «хищная» особь не находит себе пищи в течение определенного времени
(называемого временем голодной смерти), то она погибает. Время голодной
смерти является параметром.
Построенная модель исследует поведение простейшей качественной модели
экосистемы Мирового океана, состоящей из хищников и жертв. Таким образом,
«хищниками» являются акулы, «травоядными» – рыбы. Дополнительным фактором
является течение – справа налево. Об этом говорит сайт https://intellect.icu . Течение влияет на поведение рыб, на поведение
акул оно не влияет – акулы выбирают направление случайно из четырех возможных.
Если же акула находится на соседней клетке с рыбой, то она перемещается в клетку
своей жертвы, поглощая ее.
Потомство появляется и у акул и у рыб. Рыбы, как травоядные, приносят
потомство чаще, чем хищные акулы. Кроме того, время смерти акулы подобрано
таким образом, что акула приносит потомство только один раз за весь период жизни.
Особь умирает по истечении периода жизни. Если особи пришло время
«родить», но период жизни истек, особь умирает, не оставляя потомства.
Модель описывает несколько важных явлений реальной жизни, например,
процесс развития популяции на закрытом ареале (график зависимости численности от
времени ложится на так называемую логистическую кривую, см. рис. 8). По этому
графику видно, что, имея неограниченное количество пищи, популяция не будет
расти безгранично, а выйдет на некоторый постоянный уровень.

Рис. 8. Логистическая кривая
Рис. 9 Статистика поведения двух популяций
Рост популяции исследуется с точки зрения многих наук, таких как: экология,
демография, биология и др. Ключевую роль в этом вопросе играет модель
Ферхюльста, предложенная им в 1843 году:
 (1)
(1)
здесь N – количество особей в популяции, K – вместимость ареала (максимально
возможное количество особей),µ – коэффициент, характеризующий скорость роста
популяции. Это уравнение называется также логистическим, а график его решения,
соответственно, называется логистической кривой. Решение этого уравнения
выглядит следующим образом:
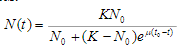
(2)
причем в момент времени t=t0
численность популяции составляла N(t0)=N0
В случае двух популяций модель описывает поведение биологического
маятника (рис. 9). На этом рисунке обе популяции находятся в равновесии, то есть
сосуществуют, взаимодействуя между собой.
Отчетливо виден пик развития популяции рыб (верхний график), далее после
добавления популяции акул (нижний) обе популяции выходят на периодические
изменения.
практическое задание к игре аква-тор
• Поместить на поле несколько рыб. Проследить динамику популяции на ареале,
получить логистическую кривую. Сопоставить с решением логистического
уравнения (1). Подобрать параметры уравнения Ферхюльста так, чтобы его
решение наилучшим образом соответствовало изменению численности
популяции.
• Поместить на поле несколько рыб и акул. Объяснить, почему со временем
численность акул не увеличивается.
• Поместить на поле несколько рыб и акул. Изменить параметр времени жизни
акулы так, чтобы акула успевала два раза принести потомство за время жизни
(параметр в интервале 21–24). Дождаться установления динамического
равновесия, оценить период и амплитуду колебаний численности популяций.
Поместить на поле несколько рыб. Позволить им размножиться. Далее
поместить несколько акул. Изменить параметры популяции акул так, чтобы
рыбы вымерли. Привести значения этих параметров.
• То же самое, но добиться вымирания акул, изменяя параметры рыб, привести
значения этих параметров.


 (1)
(1)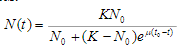 (2)
(2)
Комментарии
Оставить комментарий
Моделирование и Моделирование систем
Термины: Моделирование и Моделирование систем