Лекция
Привет, Вы узнаете о том , что такое Конечные автоматы как структуры данных - Индексируйте ключей с помощью автоматов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Конечные автоматы как структуры данных - Индексируйте ключей с помощью автоматов , настоятельно рекомендую прочитать все из категории Индексирование большого набора ключей с помощью конечных автоматов.
Конечные автоматы как структуры данных
Конечный автомат (FSM) - это набор состояний и набор переходов, которые переходят из одного состояния в другое. Одно состояние помечено как начальное, а ноль или несколько состояний помечены как конечные. Конечный автомат всегда находится только в одном состоянии.
Конечные автоматы являются довольно общими и могут использоваться для моделирования ряда процессов. Например, рассмотрим пример повседневной жизни моего кота Коши:
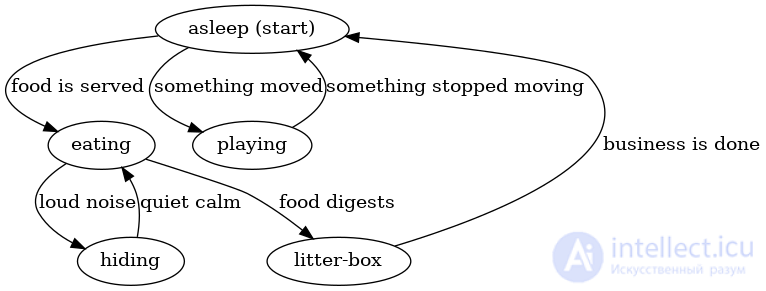
Некоторые состояния - это «спит» или «ест», а некоторые переходы - «еда подана» или «что-то перемещено». Здесь нет никаких конечных состояний, потому что это было бы излишне болезненно!
Обратите внимание, что конечный автомат приближается к нашему представлению о реальности. Коши не может одновременно играть и спать, поэтому он удовлетворяет нашему условию, что машина всегда находится только в одном состоянии за раз. Также обратите внимание, что для перехода от одного состояния к другому требуется только один ввод из среды. А именно, «засыпание» не запоминает, было ли оно вызвано усталостью от игры или чувством удовлетворения после еды. Независимо от того, как засыпал Коши, он всегда просыпается, если слышит, как что-то движется, или если звонит обеденный звонок.
Конечный автомат Коши может выполнять вычисления при заданной последовательности входных данных. Например, рассмотрим следующие входные данные:
Если мы применим эти входные данные к машине, описанной выше, то Коши будет проходить следующие состояния по порядку: «спит», «ест», «прячется», «ест», «туалетный лоток». Следовательно, если мы заметим, что еда была подана, затем последовал громкий шум, затем последовало тихое спокойствие и, наконец, пищеварение Коши, то мы могли бы сделать вывод, что Коши в настоящее время находится в лотке.
Этот особенно глупый пример демонстрирует, насколько на самом деле являются обычные конечные автоматы. Для наших целей нам нужно будет наложить несколько ограничений на тип конечного автомата, который мы используем для реализации нашего упорядоченного набора и сопоставления структур данных.
Упорядоченный набор похож на обычный набор, за исключением того, что ключи в наборе упорядочены. То есть упорядоченный набор обеспечивает упорядоченную итерацию по своим ключам. Обычно упорядоченный набор реализуется с помощью двоичного дерева поиска или btree, а неупорядоченный набор реализуется с помощью хеш-таблицы. В нашем случае мы рассмотрим реализацию, которая использует детерминированный ациклический акцептор с конечным состоянием (сокращенно FSA).
Детерминированный ациклический акцептор конечного состояния - это конечный автомат, который:
Как мы можем использовать эти свойства для представления множества? Хитрость заключается в том, чтобы хранить ключи набора в переходах машины. Таким образом, учитывая последовательность входных данных (то есть символов), мы можем определить, входит ли ключ в набор, основываясь на том, заканчивается ли оценка FSA в конечном состоянии.
Рассмотрим набор с одной клавишей jul. FSA выглядит так:

Подумайте, что произойдет, если мы спросим FSA, содержит ли он ключ «jul». Нам нужно обработать символы по порядку:
Поскольку все члены ключа были переданы в FSA, мы можем теперь спросить: находится ли FSA в конечном состоянии? Это (обратите внимание на двойной кружок вокруг состояния 3), поэтому мы можем сказать, что julэто в наборе.
Подумайте, что происходит, когда мы тестируем ключ, которого нет в наборе. Например jun:
FSA не может двигаться, потому что единственный выход из состояния 2- это l, а текущий вход - n. Поскольку l != nFSA не может следить за этим переходом. Как только FSA не может двигаться при вводе данных, он может сделать вывод, что ключа нет в наборе. Дальнейшая обработка ввода не требуется.
Рассмотрим еще один ключ ju:
В этом случае весь вход исчерпан, и FSA находится в состоянии 2. Чтобы определить, juнаходится ли он в наборе, он должен спросить, 2является ли оно конечным состоянием или нет. Поскольку это не так, он может сообщить, что juключ отсутствует в наборе.
Здесь стоит указать, что количество шагов, необходимых для подтверждения того, входит ли ключ в набор или нет, ограничено количеством символов в ключе! То есть время, необходимое для поиска ключа, никак не связано с размером набора.
Давайте добавим в набор еще один ключ, чтобы посмотреть, как он выглядит. Следующий FSA представляет собой упорядоченный набор с ключами «jul» и «mar»:
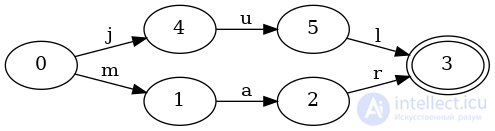
FSA стало немного сложнее. Начальное состояние 0теперь имеет два перехода: jи m. Следовательно, при наличии ключа marон сначала будет следовать за mпереходом.
Там еще одна важная вещь , чтобы заметить здесь: государство 3является общим между julи marключами. А именно, в состояние 3входят два перехода: lи r. Это разделение состояний между ключами действительно важно, потому что оно позволяет нам хранить больше информации в меньшем пространстве.
Давайте посмотрим, что произойдет, когда мы добавим junк нашему набору общий префикс с jul:
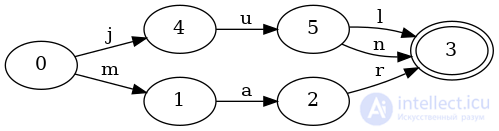
Вы видите разницу? Это небольшое изменение. Этот FSA очень похож на предыдущий. Есть только одно отличие: добавлен новый переход,, nот состояний 5к 3. Примечательно, что у FSA нет новых состояний! Поскольку оба junи julимеют общий префикс ju, эти состояния можно повторно использовать для обоих ключей.
Давайте перейдем вещи немного и посмотреть на набор со следующими ключами: october, novemberа december:

Поскольку все три ключа имеют общий суффикс ber, он кодируется в FSA только один раз. Два ключа имеют еще больший суффикс:, emberкоторый также кодируется в FSA ровно один раз.
Прежде чем перейти к упорядоченным картам, мы должны на мгновение убедиться, что это действительно упорядоченный набор. А именно, учитывая FSA, как мы можем перебирать ключи в наборе?
Чтобы продемонстрировать это, давайте воспользуемся набором, который мы создали ранее с ключами jul, junи mar:

Мы можем перечислить все ключи в наборе, пройдя весь FSA, следуя переходам в лексикографическом порядке. Например:
Этот алгоритм легко реализовать со стеком состояний для посещения и стеком переходов, которые были выполнены. Он имеет временную сложность O(n)в количестве ключей в наборе с пространственной сложностью, O(k) где k- размер самого большого ключа в наборе.
Как и в случае с упорядоченными наборами, упорядоченная карта похожа на карту, но с упорядочением, определяемым ключами карты. Как и наборы, упорядоченные карты обычно реализуются с помощью двоичного дерева поиска или btree, а неупорядоченные карты обычно реализуются с помощью хеш-таблицы. В нашем случае мы рассмотрим реализацию, в которой используется детерминированный ациклический преобразователь конечных состояний (сокращенно FST).
Детерминированный ациклический преобразователь конечного состояния - это конечный автомат, который (первые два критерия такие же, как и в предыдущем разделе):
Другими словами, FST похож на FSA, но вместо ответа «да» / «нет» для данного ключа он ответит либо «нет», либо «да, и вот значение, связанное с этим ключом».
В предыдущем разделе представлял набор, необходимый только для хранения ключей в переходах машины. Об этом говорит сайт https://intellect.icu . Машина «принимает» входную последовательность тогда и только тогда, когда она представляет собой ключ в наборе. В этом случае карта должна делать больше, чем просто «принимать» входную последовательность; ему также необходимо вернуть значение, связанное с этим ключом.
Один из способов связать значение с ключом - присоединить некоторые данные к каждому переходу. Подобно тому, как входная последовательность используется для перемещения машины из состояния в состояние, выходная последовательность может создаваться при переходе машины из состояния в состояние. Эта дополнительная «мощность» делает машину преобразователем .
Давайте посмотрим на пример карты с одним элементом jul, который связан со значением 7:

Этот автомат такой же, как и соответствующий набор, за исключением того, что первый переход jиз состояния 0в 1имеет 7связанный с ним выход . С другими переходами uи lтакже связаны выходные данные, 0которые не показаны на изображении.
Как и в случае с наборами, мы можем спросить карту, содержит ли она ключ «jul». Но нам также нужно вернуть вывод. Вот как машина обрабатывает ключевой запрос для «jul»:
Поскольку все входные данные были поданы в FST, мы можем теперь спросить: находится ли FST в конечном состоянии? Это так, мы знаем, что это julесть на карте. Кроме того, мы можем сообщить , valueкак значение , связанное с ключом jul, который 7.
Не так уж и удивительно, правда? Пример слишком упрощен. Карта с одним ключом не очень поучительна. Посмотрим, что произойдет, когда мы добавим marна карту, связанную со значением 3:
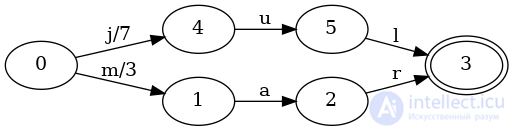
В начальное состояние вырос новый переход m, с выходом 3. Если мы найдем ключ jul, то процесс будет таким же, как и на предыдущей карте: мы вернем значение 7. Если мы ищем ключ mar, то процесс выглядит так:
Единственное изменение здесь - кроме следующих различных входных переходов - это то, что 3было добавлено valueв первом ходу. Поскольку все последующие ходы добавляют 0к value, машина сообщает 3как значение, связанное с mar.
Давайте продолжим. Что происходит, когда у нас есть ключи с общим префиксом? Рассмотрим ту же карту, что и выше, но с junдобавленным ключом, связанным со значением 6:
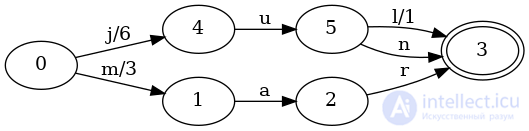
Как и в случае с наборами, был добавлен дополнительный nпереход, соединяющий состояния 5и 3. Но было еще два дополнительных изменения!
Эти изменения в выходных данных действительно важны, потому что теперь изменяются некоторые детали для поиска значения, связанного с ключом jul:
Конечное значение остается прежним 7, но мы пришли к значению иначе. Вместо того, чтобы добавлять 7начальный jпереход, мы только добавили 6, но мы дополнили 1его, добавив его в последний lпереход.
Мы также должны убедить себя, что поиск junключа тоже правильный:
Первый переход добавляет 6к value, но мы никогда не добавить ничего больше , 0чтобы valueна последующих переходах. Это потому, что junключ не проходит тот же последний lпереход, что julи. Таким образом, оба ключа имеют разные значения, но мы сделали это таким образом, чтобы большая часть структуры данных использовалась для ключей с общими префиксами.
Действительно, ключевое свойство, обеспечивающее этот обмен, заключается в том, что каждый ключ на карте соответствует уникальному пути через машину. Следовательно, всегда будет какая-то комбинация переходов, выполняемых для каждого ключа, уникального для этого конкретного ключа. Все, что нам нужно сделать, это выяснить, как расположить выходы вдоль переходов. (Мы увидим, как это сделать в следующем разделе.)
Такое совместное использование выходов работает и для ключей с общими префиксами и суффиксами. Рассмотрим ключи tuesdayи thursday, связанные со значениями 3 и 5, соответственно (для дня недели).

Обе клавиши имеют общий префикс, tи общий суффикс sday. Обратите внимание, что значения, связанные с ключами, также имеют общий префикс в отношении добавления значений. А именно, 3можно записать как 3 + 0и 5можно записать как 3 + 2. Эта идея зафиксирована в машине; общий префикс t имеет вывод 3, в то время как hпереход (которого нет в tuesday) имеет 2связанный с ним вывод . А именно, при поиске ключа будет выдан tuesdayпервый вывод t, но hпереход не будет выполняться, поэтому 2связанный с ним вывод не будет выдан. Остальные переходы имеют выход 0, который не меняет окончательный value излучается.
То, как я описал результаты, может показаться немного ограничительным; что, если они не целые? Действительно, типы выходов, которые могут использоваться в FST, ограничены вещами, в которых определены следующие операции:
Выходы также должны иметь аддитивную идентичность I, так что выполняются следующие законы:
Целые числа тривиально удовлетворяют этой алгебре (где prefixопределяется как min) с дополнительным преимуществом, заключающимся в том, что они очень малы. Можно создать и другие типы, удовлетворяющие этой алгебре, но пока мы будем работать только с целыми числами.
Нам нужно было использовать только сложение в приведенных выше примерах, но нам понадобятся две другие операции для построения FST. Это то, что мы рассмотрим дальше.
В предыдущих двух разделах я старался избегать разговоров о построении конечных автоматов, которые используются для представления упорядоченных наборов или карт. А именно, построение немного сложнее простого обхода.
Чтобы не усложнять задачу, мы накладываем ограничение на элементы в нашем наборе или карте: они должны добавляться в лексикографическом порядке. Это обременительное ограничение, но позже мы увидим, как его смягчить.
Чтобы мотивировать создание конечных автоматов, давайте поговорим о попытках .
Строительство Trie
Trie можно рассматривать как детерминированный ациклический акцептор с конечным состоянием. Поэтому все, что вы узнали в предыдущем разделе об упорядоченных наборах, применимо и к ним. Единственное различие между trie и FSA, показанными в этой статье, состоит в том, что trie разрешает совместное использование префиксов между ключами, тогда как FSA разрешает совместное использование как префиксов, так и суффиксов.
Рассмотрим набор с ключами mon, tuesи thurs. Вот соответствующий FSA, который выигрывает от совместного использования как префиксов, так и суффиксов:
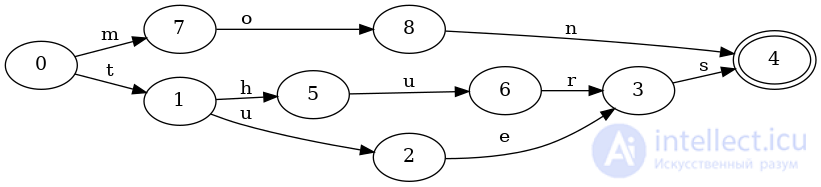
И вот соответствующее дерево, которое разделяет только префиксы:
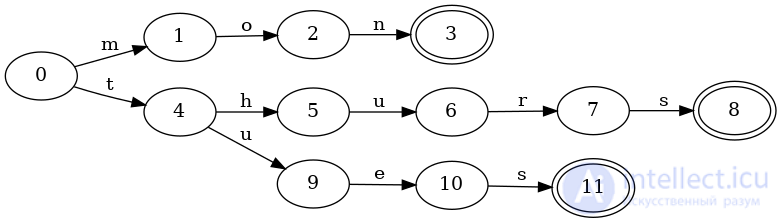
Обратите внимание, что теперь есть три различных конечных состояния и ключи tuesи thursтребуют дублирования последнего перехода sк конечному состоянию.
Построить дерево довольно просто. Учитывая новый ключ для вставки, все, что нужно сделать, это выполнить обычный поиск. Если вход исчерпан, то текущее состояние следует пометить как окончательное. Если машина останавливается до того, как ввод будет исчерпан, потому что нет действительных переходов, которым нужно следовать, просто создайте новый переход и узел для каждого оставшегося ввода. Последний созданный узел должен быть помечен как окончательный.
Строительство FSA
Напомним, что единственная разница между деревом и FSA заключается в том, что FSA разрешает совместное использование суффиксов между ключами. Поскольку дерево само по себе является FSA, мы могли бы построить дерево и затем применить общий алгоритм минимизации , который достигнет нашей цели совместного использования суффиксов.
Однако общие алгоритмы минимизации могут быть дорогими как по времени, так и по пространству. Например, дерево часто может быть намного больше, чем FSA, который разделяет структуру между суффиксами ключей. Вместо этого, если мы можем предположить, что ключи добавляются в лексикографическом порядке, мы можем добиться большего. Существенный трюк состоит в том, чтобы понять, что при вставке нового ключа любые части FSA, которые не имеют префикса с новым ключом, могут быть заморожены. А именно, никакой новый ключ, добавленный к FSA, не может уменьшить эту часть FSA.
Некоторые изображения могут помочь лучше объяснить это. Рассмотрим снова ключи mon, tuesи thurs. Поскольку мы должны добавлять их в лексикографическом порядке, мы добавим monсначала, затем, thursа затем tues. Вот как выглядит FSA после добавления первого ключа:

Это не так уж и интересно. Вот что происходит, когда мы вставляем thurs:

Вставка thursпривела к зависанию первого ключа mon,, (обозначено синим цветом на изображении). Когда определенная часть FSA была заморожена, мы знаем, что ее никогда не нужно будет изменять в будущем. А именно, поскольку все будущие ключи будут добавлены >= thurs, мы знаем, что никакие будущие ключи не будут начинаться с mon. Это важно, потому что это позволяет нам повторно использовать эту часть автомата, не беспокоясь о том, может ли она измениться в будущем. Другими словами, состояния, окрашенные в синий цвет, являются кандидатами для повторного использования другими ключами.
Пунктирные линии представляют то, что thursеще не было добавлено в FSA. Действительно, его добавление требует проверки, существуют ли какие-либо повторно используемые состояния. К сожалению, мы пока не можем этого сделать. Например, верно, что состояния 3и 8эквивалентны: оба являются окончательными и ни один из них не имеет переходов. Однако неверно, что состояние 8всегда будет равно состоянию 3. А именно, следующий ключ , который мы могли бы добавить, к примеру, быть thursday. Это изменит состояние 8на наличие dперехода, что сделает его не равным состоянию 3. Таким образом, мы пока не можем окончательно сделать вывод, как thurs выглядит ключ в автомате.
Перейдем к вставке следующего ключа tues:
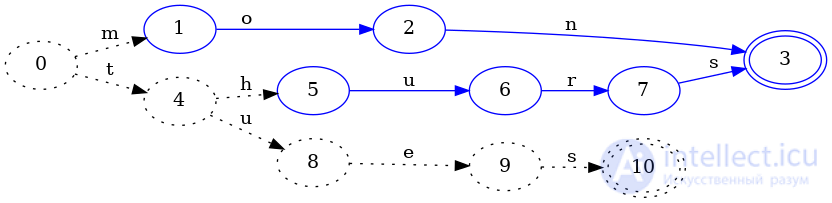
В процессе добавления tuesмы сделали вывод, что hursчасть thurs ключа могла быть заморожена. Зачем? Потому что ни один будущий ключ не может минимизировать пройденный путь, hursпоскольку ключи вставляются в лексикографическом порядке. Например, теперь мы знаем, что ключ thursdayникогда не может быть частью набора, поэтому мы можем сделать вывод, что конечное состояние thursэквивалентно конечному состоянию mon: они оба окончательные и оба не имеют переходов, и это всегда будет правдой. ,
Обратите внимание, что состояние 4осталось пунктирным: возможно, что состояние 4могло измениться при последующих вставках ключа, поэтому мы пока не можем считать его равным какому-либо другому состоянию.
Давайте добавим еще один ключ, чтобы довести дело до конца. Рассмотрим вставку zon:
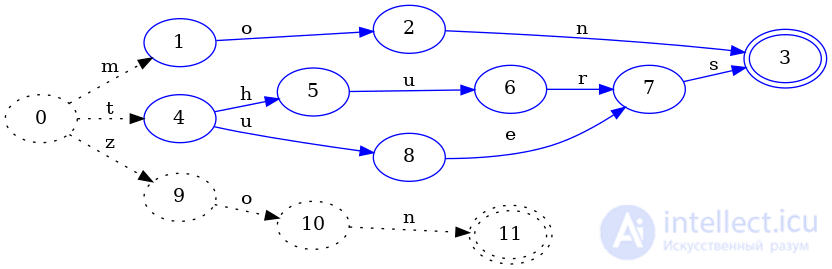
Здесь мы видим, что состояние 4было окончательно заморожено, потому что никакая последующая вставка не zonможет изменить состояние 4. Кроме того, мы также можем заключить, что thursи tuesимеют общий суффикс, и что, действительно, состояния 7и 9(из предыдущего изображения) эквивалентны, потому что ни один из них не является окончательным и оба имеют один переход с вводом, s который указывает на одно и то же состояние . Очень важно, чтобы оба их sперехода указывали на одно и то же состояние, иначе мы не сможем повторно использовать одну и ту же структуру.
Наконец, мы должны сообщить, что мы закончили вставку ключей. Теперь мы можем заморозить последнюю часть FSA zonи поискать дублирующую структуру:

И, конечно же, поскольку monи zonимеют общий суффикс, действительно существует избыточная структура. А именно, состояние 9на предыдущем изображении во всех отношениях эквивалентно состоянию 1. Это верно только потому, что состояния 10и 11также эквивалентны состояниям 2и 3. Если бы это было не так, то мы не могли бы рассматривать состояния 9и 1равенство. Например, если бы мы вставили ключ momв наш набор и по-прежнему предполагали, что состояния 9и 1равны, то результирующий FSA будет выглядеть примерно так:

И это было бы неправильно! Зачем? Потому что это FSA будет утверждать, что ключ zomнаходится в наборе, но мы никогда его не добавляли.
Наконец, стоит отметить, что описанный здесь алгоритм построения может выполняться во O(n)времени, где n- количество ключей. Легко видеть, что первоначальная вставка ключа в FST без проверки избыточной структуры не занимает больше времени, чем цикл по каждому символу в ключе, предполагая, что поиск перехода в каждом состоянии занимает постоянное время. Более сложный вопрос: как найти избыточную структуру в постоянное время? Краткий ответ - это хеш-таблица, но я объясню некоторые проблемы с ней в разделе, посвященном построению на практике .
Строительство FST
Построение детерминированной ациклической конечных преобразователей работы во многом таким же образом , как и построении детерминированных ациклических конечных акцепторов . Ключевое отличие - это размещение и совместное использование выходных данных на переходах.
Для того, чтобы сохранить низкое бремя психического, мы будем повторно использовать в качестве примера в предыдущем разделе с помощью кнопок mon, tuesи thurs. Так , F представляют собой карту, мы будем ассоциировать числовой день недели с каждой клавишей: 2, 3и 5, соответственно.
Как и раньше, начнем со вставки первого ключа mon:

(Напомним, что пунктирные линии соответствуют частям FST, которые могут измениться при последующей вставке ключа.)
Это не так интересно, но, по крайней мере, стоит отметить, что вывод 2 размещается на первом переходе. Технически такой преобразователь будет не менее правильным:
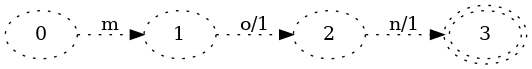
Однако размещение выходов как можно ближе к начальному состоянию значительно упрощает написание алгоритма, который разделяет выходные переходы между ключами.
Перейдем к вставке ключа, thursсопоставленного со значением 5:

Как и в случае построения FSA, вставка ключа thursпозволяет нам сделать вывод, что monчасть FST никогда не изменится. (Как показано на изображении синим цветом.)
Так как monи thursключи не имеют общий префикс , и они являются только две клавиши в карте, их все выходные значения могут быть помещены друг на первом переходе из начального состояния.
Однако, когда мы добавляем следующий ключ tues, все становится немного интереснее:
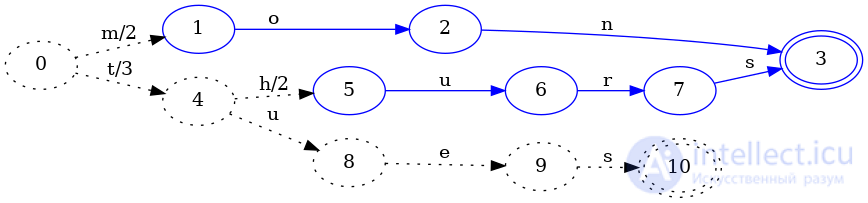
Как и в случае построения FSA, это определяет другую часть FST, которая никогда не может измениться, и замораживает ее. Разница здесь в том, что вывод при переходе из состояния 0в 4изменился с 5на 3. Это связано с тем, что tuesзначение ключа равно 3, поэтому, если начальный tпереход добавляется 5к значению, значение будет слишком большим. Мы хотим использовать как можно больше структуры, поэтому, когда мы определяем общий префикс, мы также ищем общий префикс в выходных значениях. В этом случае префиксом 5и 3является 3. Поскольку 3это значение, связанное с ключом tues, все его оставшиеся переходы могут иметь на выходе 0.
Однако, если мы изменим вывод 0->4перехода с 5на 3, значение, связанное с ключом thurs, теперь будет неправильным. Затем мы должны «отодвинуть» оставшееся значение от префикса 5и 3вниз. В этом случае 5 - 3 = 2, поэтому мы добавляем 2к каждому переходу 4(кроме нового uперехода, который мы добавили).
Таким образом, мы сохраняем выходные данные предыдущих ключей, добавляем новый выход для нового ключа и разделяем как можно больше структуры в FST.
Как и раньше, попробуем добавить еще один ключ. На этот раз давайте выберем ключ, который более интересно влияет на результаты. Давайте добавим tyeна карту и свяжем ее со значением, 99чтобы посмотреть, что произойдет.

Установка tyeключа позволила заморозить esчасть tues ключа. В частности, как и при построении FSA, мы определили эквивалентные состояния, чтобы thursи tuesмогли совместно использовать состояния в FST.
Отличие конструкции FST заключается в том, что выходной сигнал, связанный с 4->9переходом (который был только что добавлен для tyeключа), имеет выходной сигнал 96. Он выбрал, 96потому что переход до него 0->4имеет выход 3. Так как общий префикс 99и 3есть 3, вывод 0->4оставлен без изменений, а вывод для 4->9установлен в 99 - 3 = 96.
Для полноты, вот последний FST после указания, что больше никаких ключей не будет:

Единственное реальное отличие от предыдущего шага состоит в том, что последний переход tyeключа связан с конечным состоянием, общим для всех остальных ключей.
Строительство на практике
На самом деле написание кода для реализации описанных выше алгоритмов выходит за рамки этой статьи. (Его быстрая реализация, конечно, находится в свободном доступе в моей fst библиотеке.) Однако есть некоторые важные проблемы, которые стоит обсудить.
Одним из важнейших вариантов использования структуры данных FST является ее способность хранить и выполнять поиск по очень большому количеству ключей. Эта цель несколько расходится с описанным выше алгоритмом, поскольку требует, чтобы все замороженные состояния сохранялись в памяти. А именно, чтобы определить, есть ли части FST, которые можно повторно использовать для данного ключа, вы должны иметь возможность фактически искать эквивалентные состояния.
В литературе, описывающей этот алгоритм (ссылка на которую приведена в следующем разделе), говорится, что для этого можно использовать хеш-таблицу, которая обеспечивает постоянный доступ по времени к любому конкретному состоянию (при условии хорошей хэш-функции). Проблема с этим подходом заключается в том, что хеш-таблица обычно вызывает некоторые накладные расходы в дополнение к фактическому хранению всех состояний в памяти.
Можно уменьшить обременительные затраты на память, пожертвовав гарантированной минимальностью результирующего FST. А именно, можно поддерживать хеш-таблицу ограниченного размера . Это означает, что часто повторно используемые состояния сохраняются в хэш-таблице, а менее часто повторно используемые состояния удаляются. На практике хеш-таблица с примерно 10,000слотами обеспечивает достойный компромисс и близко приближается к минимальности в моих собственных ненаучных экспериментах. (Фактическая реализация немного лучше и хранит небольшой кеш LRU в каждом слоте, так что, если два общих, но разных узла сопоставляются с одним и тем же сегментом, их все равно можно использовать повторно.)
Интересным следствием использования ограниченной хеш-таблицы, в которой хранятся только некоторые состояния, является то, что построение FST может быть передано в файл на диске. А именно, когда состояния замораживаются, как описано в предыдущих двух разделах, нет причин хранить их все в памяти. Вместо этого мы можем немедленно записать их на диск (или сокет, или что-то еще).
Конечным результатом является то, что мы можем построить приблизительно минимальный FST из предварительно отсортированных ключей за линейное время и в постоянной памяти .
Ссылки
Представленные выше алгоритмы не являются моими собственными. (Насколько мне известно, я придумал идею кеширования LRU. Но это все!)
Я получил алгоритм построения FSA от инкрементального построения минимальных ациклических конечных автоматов . В частности, раздел 3 достаточно хорошо объясняет детали, но в целом документ хорошо читается.
Я получил алгоритм построения FST от Direct Construction of Minimal Acyclic Subsequential Transducers . Вся статья действительно хорошо читается, но мне пришлось перечитать ее 3-5 раз в течение недели, чтобы она действительно прониклась. В конце статьи есть псевдокод для алгоритма, то есть легко читается, когда ваш мозг привыкнет к тому, что означают все переменные.
Эти две статьи в значительной степени охватывают все, что было в статье. Тем не менее, чтобы написать эффективную реализацию, стоит прочитать больше. В частности, в этой статье не будет подробно рассмотрено, как узлы и переходы представлены в FST. Короткий ответ заключается в том, что представление FST - это последовательность байтов в памяти, и подавляющее большинство состояний занимают ровно один байт пространства. Действительно, представление конечных автоматов - активная область исследований. Вот две статьи, которые мне больше всего помогли:
Для отличного, но очень подробного и глубокого обзора данной области отлично подойдет диссертация Яна Дачука (предупреждение о PostScript в сжатом виде).
Для краткого и приятного экспериментально мотивированного обзора алгоритмов построения очень хорошо подойдет Сравнение алгоритмов построения для минимальных, ациклических, детерминированных, конечных автоматов из наборов строк .
Исследование, описанное в статье про Конечные автоматы как структуры данных - Индексируйте ключей с помощью автоматов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Конечные автоматы как структуры данных - Индексируйте ключей с помощью автоматов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Индексирование большого набора ключей с помощью конечных автоматов
Комментарии
Оставить комментарий
Индексирование большого набора ключей с помощью конечных автоматов
Термины: Индексирование большого набора ключей с помощью конечных автоматов