Лекция
Привет, Вы узнаете о том , что такое асимптотическое поведение функции восстановления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое асимптотическое поведение функции восстановления, элементарная теорема восстановления , настоятельно рекомендую прочитать все из категории вероятностные процессы.
Теперь исследуем асимптотическое поведение функции восстановления при t→∞.
ТЕОРЕМА 2.1. Для простого процесса восстановления при t→∞ имеет место следующее асимптотическое разложение
, 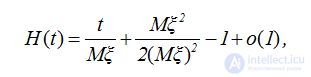 (2.22)
(2.22)
если существует математическое ожидание и второй момент.
ДОКАЗАТЕЛЬСТВО. При доказательстве используется тауберова теорема, формулировка которой приведена в математическом приложении 3. Об этом говорит сайт https://intellect.icu . Для того чтобы воспользоваться этой теоремой, необходимо построить разложение функции H*(s) при s→0. В рассматриваемом случае
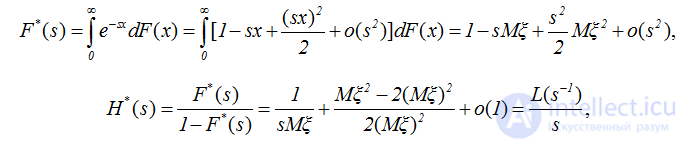
где обозначены
, 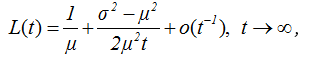 (2.23)
(2.23)
μ= Mξ, σ2=Mξ2-(Mξ)2.
Далее необходимо проверить, является ли функция L(t) медленно меняющейся на бесконечности, то есть имеет ли место равенство
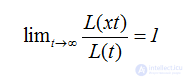
при любом положительном x. Последнее равенство для функции (2.23) очевидно. Таким образом, все условия тауберовой теоремы выполняются. Следовательно, при t→∞
,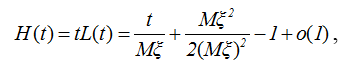
что и доказывает утверждение теоремы.*
Доказанную теорему называют элементарной теоремой восстановления и дают ее в форме следующего утверждения .
Сделаем два замечания к доказанной теореме.
Замечание 1. Почти дословное повторение доказательства для функции восстановления H1(t) дает следующее асимптотическое разложение при t→∞
.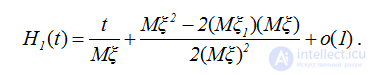
Из последнего равенства можно заключить, что главный член разложения не зависит от распределения F1(t). Последнее разложение будет получено также ниже с использованием узловой теоремы восстановления.
Замечание 2. Для плотностей восстановления очевидны равенства
.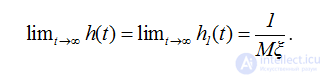
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области асимптотическое поведение функции восстановления имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое асимптотическое поведение функции восстановления, элементарная теорема восстановления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Из статьи мы узнали кратко, но содержательно про асимптотическое поведение функции восстановления
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы