Мартингалы, субмартингалы, супермартингалы. Примеры. Разложение Дуба.

Привет, мой друг, тебе интересно узнать все про мартингалы, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое мартингалы, субмартингалы, супермартингалы, теорема дуба о разложении , настоятельно рекомендую прочитать все из категории вероятностные процессы.

мартингалы , субмартингалы , супермартингалы . Примеры. Разложение Дуба.

§ 3 Мартингалы, супермартингалы, субмартингалы.

3.1. Пусть (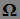,,,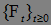Р) – стохастический базис, последовательность { 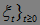- согласована с потоком 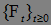, и принимает значения в .

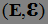Определение. Последовательность (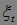,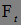)_t>1 называется мартингалом, если:
1) 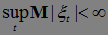, 2)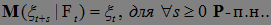

Если выполнено 1) и 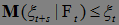Р -п. н., то последовательность (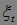,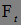)_t>0 называется супермартингалом.

Если выполнено 1) и 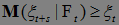Р - п. н., то последовательность (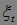,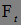)_t>0 называется субмартингалом.

Пример. Пусть 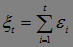, где 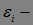независимые в совокупности случайные величины. Пусть 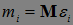, 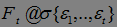. Ясно, что

=

=++ +.

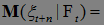
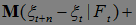
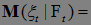
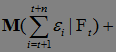
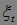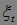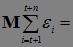
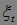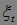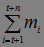Отсюда следует, что:

а) (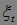,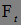)_t>1- мартингал, если 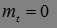для любого t;

б) (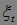,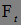)_t>1- супермартингал, если 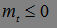для любого t;

в) (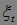,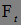)_t>1- субмартингал, если 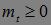для любого t;

Утверждение 5. Если (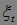,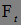)_t>0– марковская случайная последовательность с переходной вероятностью P(s,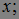,t,B), то
P(s, 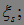t,B) – мартингал для , относительно потока 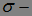алгебр и меры Р.

Доказательство. Из соотношения Чепмена – Колмогорова имеем
Р-п. н. при :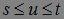

M(P(u, 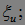,t,B)|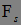)=M(P(u, 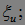,t,B)| ) = .

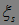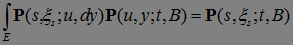3.2. Теорема 6 (Дуба). Пусть (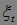,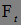)_t>0 – неотрицательный супермартингал, тогда с вероятностью 1 существует .

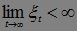Замечания. 1) Покажем, что предложения о неотрицательности супермартингала (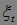,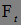)_t>0 можно отказаться. Очевидно, что 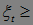ММ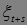, т.е. в среднем последовательность 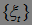- убывает. Пусть 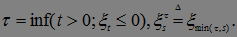Образуем новую последовательность 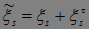. Понятно, что 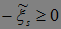.Тогда 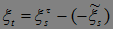, значит любой супермартингал представим в виде разности двух неотрицательных супермартингалов.

2) Если 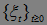- супермартингал, то 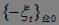- субмартингал. Поэтому утверждение теоремы 6 верно и для субмартингалов.

3.2.1 Доказательство теоремы Дуба опирается на две вспомогательные леммы.

Пусть 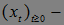числовая последовательность, a<b, [a,b] – отрезок. Обозначим 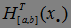- число пересечений отрезка [a,b] последовательностью 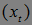снизу вверх.

Лемма 7 (О числе пересечений отрезка [a,b] снизу вверх).

Справедливо неравенство:

,

где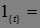

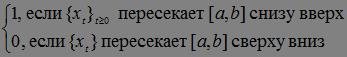
Доказательство. Обозначим

, ,

, ,

,

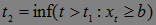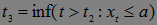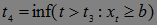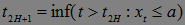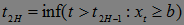
Очевидно, что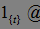

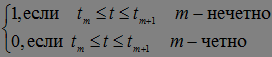
Отсюда следует, что

(b-a) =.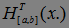

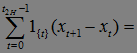
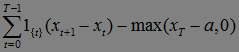Докзательство закончено.

Лемма 8. (О среднем числе пересечений). Об этом говорит сайт https://intellect.icu . Пусть (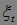,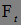)_t>0– неотрицательный супермартингал, тогда М.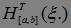

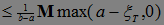Доказательство. В силу леммы 7 имеем неравенство:

.

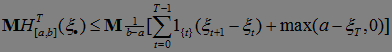Так как (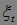,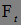)_t>0 - супермартингал, то М() ≤ 0. Отсюда следует неравенство

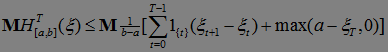
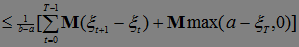
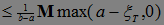. Доказательство закончено.

3.2.2. Доказательство теоремы 6. Предположим, что у последовательности 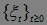не существует конечного предела. Через В обозначим множество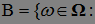 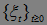не имеет конечного предела}. Наше предположение выполнено, если:

1) 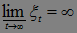Р - п. н.,

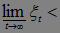
2) 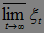Р - п. н.

Обозначим: А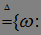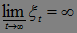}, C=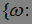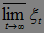}. Очевидно, что 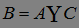, поэтому 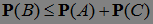. Значит для доказательства теоремы достаточно доказать, что Р(А) =0 и Р(С)=0.

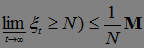
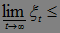
Покажем, что Р(А)=0. В силу неравенства Чебышева и леммы Фату имеем Р(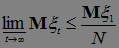. Устремляя теперь 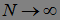, получаем Р(А)=0.

Теперь докажем, что Р(С)=0. Заметим, что

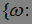
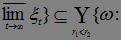
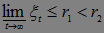
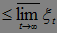, где и - рациональные числа}==.

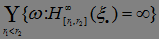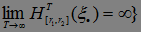Рассмотрим вероятность Р(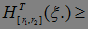N) в силу неравенства Чебышева и леммы 8 мы имеем:

Р(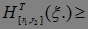N).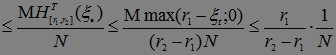

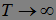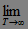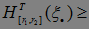Устремляя теперь , получаем неравенство Р(N)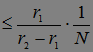. Отсюда следует, что Р(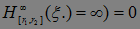, т.е.Р(С)=0. Доказательство закончено.

3.3. Определение. Мартингал называется равномерно интегрируемым, если .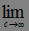

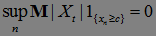Теорема 9. Пусть равномерно интегрируемый мартингал, тогда Р -п.н. существует случайная величина 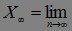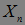такая, что:

а) 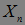= Р - п. н.,

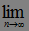б) М|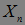- 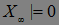Р - п. н.

Доказательство этой теоремы следует из теоремы 6.

Мартинга́л Ду́ба в теории случайных процессов — это случайный процесс, построенный достаточно общим образом, который всегда оказывается мартингалом.

Пусть дана произвольная последовательность случайных величин . Пусть случайная величина такова, что ее математическое ожидание конечно: . Определим последовательность

.

Тогда случайный процесс является мартингалом и называется мартингалом Дуба.

теорема дуба о разложении

В теории случайных процессов в дискретном времени , являющейся частью математической теории вероятностей , теорема о разложении Дуба дает уникальное разложение каждого адаптированного и интегрируемого случайного процесса в виде суммы мартингала и предсказуемого процесса (или «дрейфа»). начиная с нуля. Теорема была доказана Джозефом Л. Дубом и названа в его честь .

Аналогичная теорема в случае непрерывного времени - это теорема Дуба – Мейера о разложении .

утверждение

Пусть (Ω,  F , ℙ) - вероятностное пространство , I = {0, 1, 2 ,. . . , N } с N ∈ ℕ или я = ℕ ₀ конечное или бесконечное множество индексов, ( F _п ) _{п ∈ Я} фильтрации из F , и Х = ( Х _п ) _{п ∈ Я} адаптированный случайный процесс с E [| X _п |] <∞ для всех п ∈ I . Тогда существует мартингал М = ( М _п ) _{п ∈ I} и интегрируемый предсказуемый процесс A = ( A _п ) _{п ∈ I} , начиная с A ₀ = 0 , так что Х _п = М _п + _п для любого п ∈ I . Здесь предсказуемые означает , что _п является F _{п -1} - измеримы для любого п ∈ I \ {0 }. Это разложение почти наверняка единственное.

Замечание

Теорема дословно справедлива также для случайных процессов X, принимающих значения в d -мерном евклидовом пространстве ℝ ^d или комплексном векторном пространстве ℂ ^d . Это следует из одномерного варианта при индивидуальном рассмотрении компонентов.

Доказательство

Существование

Используя условные ожидания , определите процессы A и M для каждого n ∈ I явно как

1

и2

где суммы для п = 0 являются пустыми и определяется как ноль. Здесь A складывает ожидаемые приращения X , а M складывает неожиданности, т. Е. Ту часть каждого X _k, которая не известна на один временной шаг раньше. Из этих определений, А _{п + 1} (если п + 1 ∈ I ) и М _п есть Р _п -измеримой , потому что процесс Х приспособлен, Е [| A _n |] <∞ и E [| М _п |] <∞ , так как процесс X интегрируем, и разложение X _п = М _п + _п справедлива для любого п ∈ I . Мартингейл недвижимость

так как

также следует из приведенного выше определения ( 2 ) для любого n ∈ I \ {0 }.

Уникальность

Чтобы доказать единственность, пусть X = M ' + A ' - дополнительное разложение. Тогда процесс Y : = M - M ' = A ' - A является мартингалом, из чего следует, что

так как,

а также предсказуемым, подразумевая, что

так как

для любого n ∈ I \ {0 }. Поскольку Y ₀ = A ' ₀ - A ₀ = 0 по соглашению о начальной точке предсказуемых процессов, это итеративно означает, что Y _n = 0 почти наверняка для всех n ∈ I , следовательно, разложение почти наверняка единственное.

Следствие

Вещественнозначный случайный процесс X является субмартингалом тогда и только тогда, когда он имеет разложение Дуба на мартингал M и интегрируемый предсказуемый процесс A, который почти наверняка возрастает . Это супермартингейл тогда и только тогда, когда A почти наверняка убывает .

Доказательство

Если X - субмартингал, то

так как

для всех k ∈ I \ {0 }, что равносильно утверждению, что каждый член в определении ( 1 ) оператора A почти наверняка положителен, следовательно, A почти наверняка возрастает. Аналогично доказывается эквивалентность для супермартингалов.

пример

Пусть X = ( X _n ) _{n ∈ℕ 0} - последовательность независимых интегрируемых вещественных случайных величин. Они адаптированы к фильтрации, порождаемой последовательностью, т. Е. F _n = σ ( X ₀ , ..., X _n ) для всех n ∈ ℕ ₀ . Согласно ( 1 ) и ( 2 ) разложение Дуба задается формулой

и

Если случайные величины исходной последовательности X имеют нулевое среднее значение, это упрощается до

и

следовательно, оба процесса являются (возможно, неоднородными по времени) случайными блужданиями . Если последовательность X = ( X _n ) _{n ∈ℕ 0} состоит из симметричных случайных величин, принимающих значения +1 и −1 , то X ограничено, но мартингал M и предсказуемый процесс A являются неограниченными простыми случайными блужданиями (а не равномерно интегрируемо ), и теорема Дуба о необязательной остановке может быть неприменима к мартингалу M, если время остановки не имеет конечного ожидания.

заявка

В финансовой математике теорема о разложении Дуба может использоваться для определения наибольшего оптимального времени исполнения американского опциона . Пусть X = ( X ₀ , X ₁ , ..., X _N ) обозначает неотрицательные дисконтированные выплаты американского опциона в N- периодной модели финансового рынка, адаптированной к фильтрации ( F ₀ , F ₁ ,. ..., F _N ) , и пусть ℚ обозначает эквивалентную мартингальную меру . Пусть U = ( U ₀ , U ₁ ,..., U _N ) обозначим Snell конверт из X по отношению к ℚ . Конверт Снелла - это наименьший ℚ- супермартингейл, доминирующий над X, и на полноценном финансовом рынке он представляет собой минимальную сумму капитала, необходимую для хеджирования американского опциона до погашения. Пусть U = M + A обозначает разложение Дуба относительно with оболочки Снеллиуса U на мартингал M = ( M ₀ , M ₁ , ..., M _N ) и убывающий предсказуемый процесс A = ( A ₀ , A ₁ , ..., A _N ) с A ₀ = 0 . Тогда наибольшее время остановки для оптимального исполнения американского опциона составляет

Поскольку A предсказуемо, событие { τ _max = n } = { A _n = 0, A _{n +1} <0 } находится в F _n для любого n ∈ {0, 1,. . . , N - 1 }, поэтому τ _max действительно время остановки. Это последний момент перед тем, как дисконтированная стоимость американского опциона упадет в ожидании; до момента τ _max процесс дисконтированной стоимости U является мартингалом по отношению к ℚ .

Обобщение

Теорема Дуба о разложении может быть обобщена с вероятностных пространств на σ-конечные пространства с мерой .

Напиши свое отношение про мартингалы. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое мартингалы, субмартингалы, супермартингалы, теорема дуба о разложении и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы