2.9. Примеры использования узловой теоремы восстановления кратко

Привет, Вы узнаете о том , что такое примеры использования узловой теоремы восстановления , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое примеры использования узловой теоремы восстановления , настоятельно рекомендую прочитать все из категории вероятностные процессы.

2.9. примеры использования узловой теоремы восстановления

1. Вычисление предельных распределений прямого и обратного времен возвращения.

Для обратного времени возвращения нужно перейти к пределу в соотношении (2.39), воспользовавшись узловой теоремой восстановления. Верхний предел определенного интеграла в (2.39) равен t-x, поэтому под знаком интеграла стоит функция Q(t-x-y)=1-F(t+x-x-y)=1-F(t-y). Следовательно, имеем Q(t)=1-F(t+x). Предел первого слагаемого равен единице и окончательно получаем

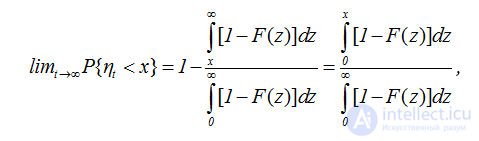, (2.47)

потому что

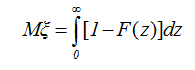(2.48)

(более подробно см. в математическом приложении 4).

Следовательно, плотность предельного распределения равна

.

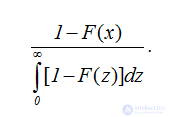
Для прямого времени возвращения нужно перейти к пределу в соотношении (2.41), используя узловую теорему восстановления. Верхний предел определенного интеграла в (2.41) равен t, поэтому под знаком интеграла стоит функция Q(t-y)=1-F(t+x-y). Следовательно, имеем Q(t)=1-F(t+x).

Предел первого слагаемого равен единице и окончательно получаем

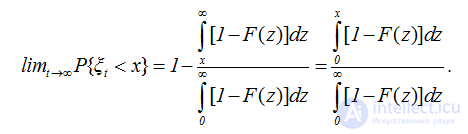. (2.49)

Таким образом, доказано совпадение предельных распределений для прямого и обратного времен возвращения.

2. Об этом говорит сайт https://intellect.icu . Вычисление предельного совместного распределения прямого и обратного времен возвращения.

Для определения предельного совместного распределения нужно перейти к пределу в равенстве (2.44). В этом случае Q(t)=1-F(t+x+y) и поэтому

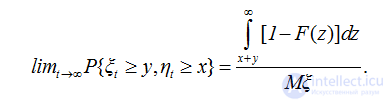(2.50)

Обратим внимание на зависимость случайных величин ξ_t и η_t и в предельном случае. Последнее утверждение следует из равенства (2.50).

Теперь для предельного случая определим математическое ожидание интервала, накрывающего бесконечно далекую точку t. Величина этого интервала равна ξ_t+η_t. Если воспользоваться равенством (2.48) для математического ожидания положительной случайной величины и предельными равенствами (2.42) и (2.44), то можно утверждать, что математическое ожидание этого интервала равно

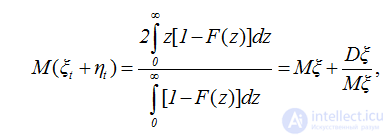(2.51)

где через Dξ обозначена дисперсия случайной величины, если таковая существует. Как следует из равенства (2.51), математическое ожидание исследуемого интервала не совпадает с математическим ожиданием Mξ и отличается тем больше, чем больше дисперсия случайной величины ξ. При выводе равенства (2.51) мы воспользовались свойством математического ожидания суммы даже зависимых слагаемых. Тот же самый результат получим, если непосредственно перейдем к пределу в равенстве (2.39).

3. Вычисление предельного распределения суммы прямого и обратного времен возвращения (распределения интервала, накрывающего бесконечно далекий момент).

Для определения этого предельного распределения нужно перейти к пределу в равенстве (2.45). Равенство (2.45) можно преобразовать заменой переменной интегрирования z=t-ν

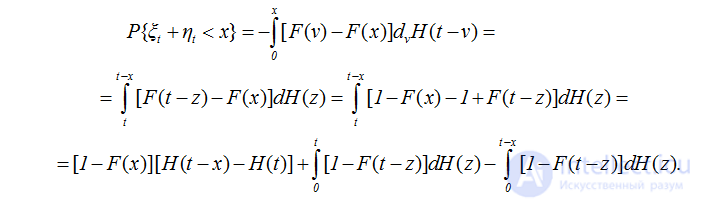
Первое слагаемое имеет предел, равный 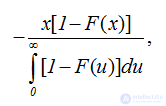на основании теоремы Блекуэлла, второе слагаемое имеет пределом единицу, так как справедливо равенство

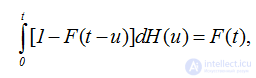если воспользоваться интегральным уравнением восстановления (2.16) или узловой теоремой восстановления, наконец, последнее слагаемое имеет пределом если использовать узловую теорему восстановления.

Окончательно получаем

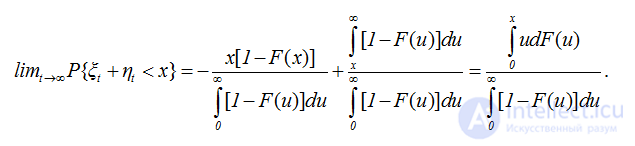(2.52)

4. Построение асимптотического разложения функции восстановления процесса восстановления с запаздыванием.

Из равенства (2.18) элементарными преобразованиями получаем

.

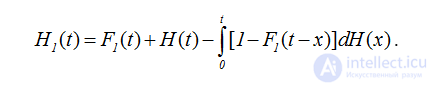
Для функции H(t) воспользуемся асимптотическим разложением (2.22), а для последнего интеграла на основании узловой теоремы имеем

.

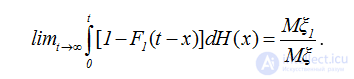
Поэтому для функции восстановления процесса восстановления с запаздыванием получаем

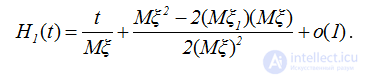. (2.53)

В заключение настоящего раздела еще раз отметим, что полученные формулы для предельных распределений справедливы при неарифметическом (нерешетчатым) распределении F(x).

Вау!! 😲 Ты еще не читал? Это зря!

• Случайная мера Пуассона
• случайный процесс
• случайные блуждания
• процесс восстановления
• модель Крамера-Лундберга
• эмпирические меры
• пуассоновская случайная мера

Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области примеры использования узловой теоремы восстановления имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое примеры использования узловой теоремы восстановления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы

Из статьи мы узнали кратко, но содержательно про примеры использования узловой теоремы восстановления