Лекция
Привет, мой друг, тебе интересно узнать все про метод монте-карло, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое метод монте-карло , настоятельно рекомендую прочитать все из категории вероятностные процессы.
Методы Монте-Карло (ММК) — группа численных методов для изучения случайных процессов. Суть метода заключается в следующем: процесс описывается математической моделью с использованием генератора случайных величин, модель многократно обсчитывается, на основе полученных данных вычисляются вероятностные характеристики рассматриваемого процесса. Например, чтобы узнать методом Монте-Карло, какое в среднем будет расстояние между двумя случайными точками в круге, нужно взять координаты большого числа случайных пар точек в границах заданной окружности, для каждой пары вычислить расстояние, а потом для них посчитать среднее арифметическое.
Методы используются для решения задач в различных областях физики, химии, математики, экономики, оптимизации, теории управления и др.
Название метода происходит от района Монте-Карло, известного своими казино.
метод монте-карло имеет множество различных приложений. Он применяется в следующих областях: в промышленности для моделирования изменчивости производственных процессов; в физике, химии и биологии для моделирования разнообразных явлений; в области игр для моделирования искусственного интеллекта, например, в китайской игре го; в области финансов для оценки производных финансовых инструментов и опционов. По сути, метод Монте-Карло используется везде.
Современный вариант метода сформировался в рамках Манхэттенского проекта, где он применялся для моделирования расстояний, которые могут пройти нейтроны в различных материалах. Идея моделирования на основе генерации набора случайных значений существовала уже в течение некоторого времени, но особое развитие получила при создании атомной бомбы, распространившись затем во многих других областях знаний.
Большим преимуществом метода Монте-Карло является то, что он позволяет учесть в модели элемент случайности и сложность реального мира. Кроме того, метод является робастным по отношению к изменению различных параметров, таких как распределение случайной величины. В его основе лежит закон больших чисел.
Одним из типичных примеров использования метода Монте-Карло являются задачи, в которых необходимо найти математическое ожидание некоторой случайной величины. Для этого нужно сгенерировать набор случайных значений данной величины и найти среднее. Случайная величина обычно характеризуется определенным распределением вероятностей.
Суть метода заключается в следующем: для целевой случайной величины генерируется набор случайных значений, а затем на его основе рассчитываются требуемые значения.
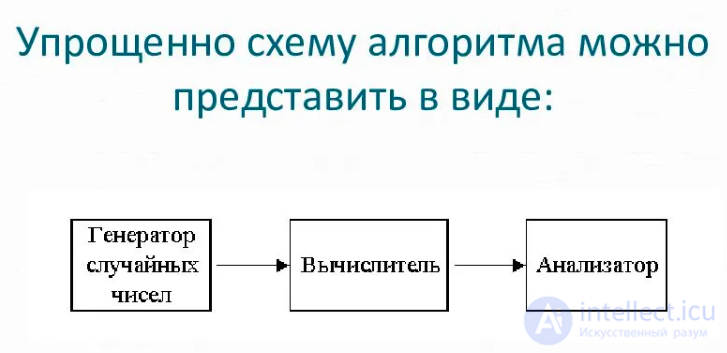
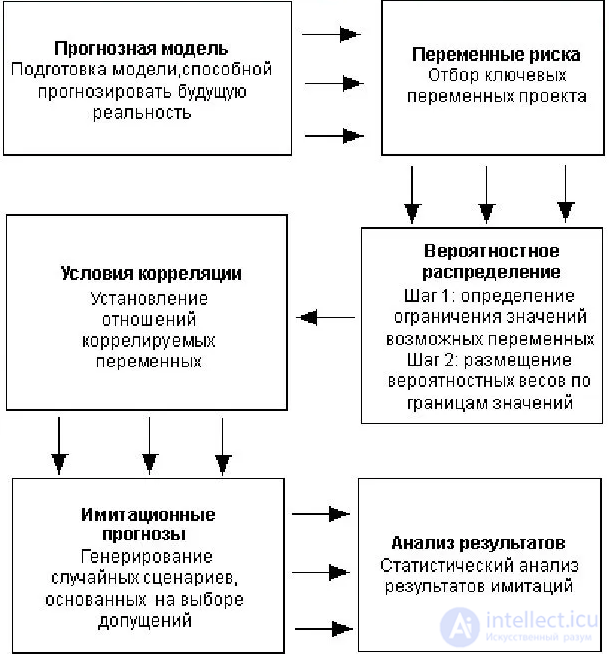
Сущность метода Монте-Карло состоит в следующем: требуется найти значение А некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой равно А: М(Х)= A. Практически же поступают так: производят N испытаний, в результате которых получают N возможных значений X, вычисляют их среднее арифметическое и принимают его в качестве оценки (приближенного значения) A ’ искомого числа A. Как правило, составляется программа для осуществления одного случайного испытания. Погрешность вычислений, как правило, пропорциональна D/ sqrt (N), где D – некоторая постоянная. Это значит, что N должно быть велико, поэтому метод существенно опирается на возможности ЭВМ. Ясно, что добиться таким путем высокой точности невозможно. Это один из недостатков метода. Во многих задачах удается значительно увеличить точность, выбрав способ расчета, которому соответствует значительно меньшее D.
В отличие от аналитических методов, ищущих решение в виде ряда по собственным функциям, методы Монте-Карло ищут решения в виде статистических сумм. Для их применения достаточно описания вероятностного процесса и не обязательна его формулировка в виде интегрального уравнения; оценка погрешности чрезвычайно проста, их точность слабо зависит от размерности пространства. В этом я убедился, проведя опыты для решения двух простых задач. Результаты опытов показали свою точность, поэтому с помощью метода Монте-Карло решаются многие сложные задачи, которые очень сложно или не возможно решить другими методами
Случайные величины использовались для решения различных прикладных задач достаточно давно. Примером может служить способ определения числа Пи, который был предложен Бюффоном еще в 1777 году. Суть метода была в бросании иглы длиной на плоскость, расчерченную параллельными прямыми, расположенными на расстоянии
друг от друга (см. Рис. 1).
Вероятность (как видно из дальнейшего контекста, речь идет не о вероятности, а о математическом ожидании количества пересечений за один опыт; вероятностью это становится лишь при условии ) того, что отрезок пересечет прямую, связана с числом Пи:
где
Этот интеграл просто взять: (при условии, что
), поэтому подсчитав долю отрезков, пересекающих прямые, можно приближенно определить это число. При увеличении количества попыток точность получаемого результата будет увеличиваться.
В 1864 году капитан Фокс, выздоравливая после ранения, чтобы как-то занять себя, реализовал эксперимент по бросанию иглы . Результаты представлены в следующей таблице:
| Число бросаний | Число пересечений | Длина иглы | Расстояние между прямыми | Вращение | Значение Пи | Ошибка | |
|---|---|---|---|---|---|---|---|
| Первая попытка | 500 | 236 | 3 | 4 | отсутствует | 3.1780 | +3,6⋅10-2 |
| Вторая попытка | 530 | 253 | 3 | 4 | присутствует | 3.1423 | +7,0⋅10-4 |
| Третья попытка | 590 | 939 | 5 | 2 | присутствует | 3.1416 | +4,7⋅10-5 |
Комментарии:
С помощью метода Монте-Карло можно вычислить число Пи.
Вписав круг в квадрат (диаметр круга равен стороне квадрата), можно выразить отношение площади круга к площади квадрата следующим образом:
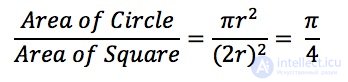
Если мы сможем вычислить это отношение, значит, мы сможем получить значение числа Пи.
Заполним квадрат точками со случайными координатами. Рассчитаем отношение количества точек, попавших в круг, к общему количеству точек. Умножим результат на 4, чтобы получить значение числа Пи.

Чем больше количество точек, тем ближе полученное значение к истинному значению числа Пи.
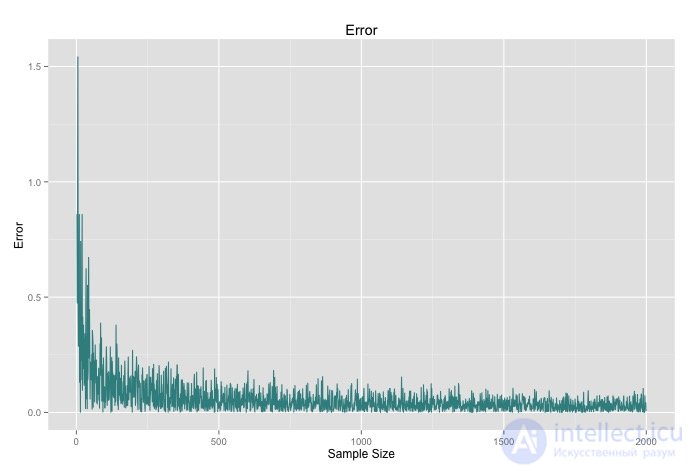
Этот простой пример демонстрирует метод Монте-Карло в действии.
пример на языке R
|
# estimating pi using Monte Carlo methods. This code won't run perfectly for you, because I # didn't save everything I did, like adding vectors to a dataframe named Pi. |
|
| # Just the important stuff is here. | |
| center <- c(2.5, 2.5) # the center of the circle | |
| radius <- 2.5 | |
| distanceFromCenter <- function(a) { | |
| sqrt(sum((center - a) ^ 2)) | |
| } | |
| # let's define a 5 by 5 square matrix | |
| points <- c(0,0, 0,5, 5,5, 5,0) | |
| square <- matrix(points, nrow = 4, ncol = 2, byrow = TRUE) | |
| # now all I need to do is make matrix A a matrix of real simulated points. | |
| n <- 100 # number of points | |
| A <- matrix(runif(n*2, min=0, max=5), nrow = n, ncol = 2, byrow = T) # random sampling occurs here!!! | |
| ## An alternate way to generate randoms, with faster convergence | |
| # library(randtoolbox) | |
| # A <- matrix(5*halton(n*2), nrow = n, ncol = 2, byrow = T) | |
| # here's how you'll test if it's in the circle. Об этом говорит сайт https://intellect.icu . | |
| b <- apply(A, 1, distanceFromCenter) | |
| # d <- subset(b, b < radius) # if you know a better way to do this part, email me. | |
| # num <- length(d) / length(b) | |
| num <- mean(b < radius) | |
| piVec <- c() | |
| for (i in 1:2000) { | |
| n <- i | |
| A <- matrix(runif(n*2, min=0, max=5), nrow = n, ncol = 2, byrow = T) | |
| b <- apply(A, 1, distanceFromCenter) | |
| d <- subset(b, b < radius) | |
| num <- length(d) / length(b) | |
| piVec[i] = num*4 | |
| } | |
| library(data.table) | |
| Pi <- data.frame(piVec) | |
| Pi <- data.table(Pi) | |
| Pi[, ind := seq(0, 1999)] | |
| Pi[, error := abs(pi - piVec)] | |
| Pi <- data.frame(Pi) | |
| names(Pi) <- c("guess", "ind", "error") | |
| ##### Graphing the error | |
| # note - if you want this part to work for you, you'll have to create the appropriate data frame from the piVec vector. | |
| library(ggplot2) | |
| ggplot(Pi, aes(x = ind, y = error)) + | |
| geom_line(colour = '#388E8E') + | |
| ggtitle("Error") + | |
| xlab("Sample Size") + | |
| ylab("Error") | |
Создание математического аппарата стохастических методов началось в конце XIX века. В 1899 году лорд Релей показал, что одномерное случайное блуждание на бесконечной решетке может давать приближенное решение одного из видов параболического дифференциального уравнения . Андрей Николаевич Колмогоров в 1931 году дал большой толчок развитию стохастических подходов к решению различных математических задач, поскольку он сумел доказать, что цепи Маркова связаны с некоторыми интегро-дифференциальными уравнениями. В 1933 году Иван Георгиевич Петровский показал, что случайное блуждание, образующее Марковскую цепь, асимптотически связано с решением эллиптического дифференциального уравнения в частных производных. После этих открытий стало понятно, что стохастические процессы можно описывать дифференциальными уравнениями и, соответственно, исследовать при помощи хорошо на тот момент разработанных математических методов решения этих уравнений.
Сначала Энрико Ферми в 1930-х годах в Италии, а затем Джон фон Нейман и Станислав Улам в 1940-х в Лос-Аламосе предположили, что можно использовать связь между стохастическими процессами и дифференциальными уравнениями «в обратную сторону». Они предложили использовать стохастический подход для аппроксимации многомерных интегралов в уравнениях переноса, возникших в связи с задачей о движении нейтрона в изотропной среде.
Идея была развита Уламом, который, раскладывая пасьянсы во время выздоровления после болезни, задался вопросом, какова вероятность того, что пасьянс сложится. Вместо того, чтобы использовать обычные для подобных задач соображения комбинаторики, Улам предположил, что можно просто поставить эксперимент большое число раз и, подсчитав число удачных исходов, оценить вероятность. Но из-за необходимости проведения большого количества однотипных экспериментальных действий метод не получил большого распространения.
С появлением первого электронного компьютера ENIAC, который мог с большой скоростью генерировать псевдослучайные числа и использовать их в математических моделях, возобновился интерес к стохастическим методам. Станислав Улам обсудил свои идеи с Джоном фон Нейманом, который в конечном итоге использовал ENIAC для предложенного Уламом метода статистического отбора при решении различных проблем перемещения нейтронов . Из-за необходимости в конце 1946 года выключить ENIAC на значительное время, для продолжения исследований перемещения нейтронов Энрико Ферми даже разработал специализированный аналоговый компьютер, которому дали имя FERMIAC (по аналогии с ENIAC, но с указанием на авторство Ферми), где также был на механическом уровне реализован метод Монте-Карло.
После начала использования компьютеров произошел большой прорыв, и метод Монте-Карло применялся во многих задачах, для решения которых стохастический подход оказался более эффективным, чем другие математические методы. Тем не менее, использование такой методики имело и свою ограниченность из-за необходимости очень большого количества вычислений для получения результатов с высокой точностью.
Годом рождения термина «метод Монте-Карло» считается 1949 год, когда в свет вышла статья Метрополиса и Улама «Метод Монте-Карло». Название метода происходит от названия коммуны в княжестве Монако, широко известного своими многочисленными казино, поскольку именно рулетка является одним из самых широко известных генераторов случайных чисел. Станислав Улам пишет в автобиографии «Приключения математика», что название было предложено Николасом Метрополисом в честь его дяди, который был азартным игроком.
В 1950-х годах метод использовался для расчетов при разработке водородной бомбы. Основные заслуги в развитии метода в это время принадлежат сотрудникам лабораторий ВВС США и корпорации RAND. Одними из первых Метод Монте-Карло для расчета ливней частиц применили советские физики А. А. Варфоломеев и И. А. Светлолобов .
В 1970-х годах в новой области математики — теории вычислительной сложности было показано, что существует класс задач, сложность (количество вычислений, необходимых для получения точного ответа) которых растет с размерностью задачи экспоненциально. Иногда можно, пожертвовав точностью, найти алгоритм, сложность которого растет медленнее, но есть большое количество задач, для которого этого нельзя сделать (например, задача определения объема выпуклого тела в n-мерном евклидовом пространстве) и метод Монте-Карло является единственной возможностью для получения достаточно точного ответа за приемлемое время.
В настоящее время основные усилия исследователей направлены на создание эффективных Монте-Карло алгоритмов различных физических, химических и социальных процессов для параллельных вычислительных систем.
Предположим, необходимо взять интеграл от некоторой функции. Воспользуемся неформальным геометрическим описанием интеграла и будем понимать его как площадь под графиком этой функции.
Для определения этой площади можно воспользоваться одним из обычных численных методов интегрирования: разбить отрезок на подотрезки, подсчитать площадь под графиком функции на каждом из них и сложить. Предположим, что для функции, представленной на рисунке 2, достаточно разбиения на 25 отрезков и, следовательно, вычисления 25 значений функции. Представим теперь, мы имеем дело с -мерной функцией. Тогда нам необходимо
отрезков и столько же вычислений значения функции. При размерности функции больше 10 задача становится огромной. Поскольку пространства большой размерности встречаются, в частности, в задачах теории струн, а также многих других физических задачах, где имеются системы со многими степенями свободы, необходимо иметь метод решения, вычислительная сложность которого бы не столь сильно зависела от размерности. Именно таким свойством обладает метод Монте-Карло.
Предположим, требуется вычислить определенный интеграл
Рассмотрим случайную величину , равномерно распределенную на отрезке интегрирования
. Тогда
также будет случайной величиной, причем ее математическое ожидание выражается как
где — плотность распределения случайной величины
, равная
на участке
. Таким образом, искомый интеграл выражается как
но математическое ожидание случайной величины можно легко оценить, смоделировав эту случайную величину и посчитав выборочное среднее.
Итак, бросаем точек, равномерно распределенных на
, для каждой точки
вычисляем
. Затем вычисляем выборочное среднее:
. В итоге получаем оценку интеграла:
Точность оценки зависит только от количества точек .
Этот метод имеет и геометрическую интерпретацию. Он очень похож на описанный выше детерминистический метод, с той разницей, что вместо равномерного разделения области интегрирования на маленькие интервалы и суммирования площадей получившихся «столбиков» мы забрасываем область интегрирования случайными точками, на каждой из которых строим такой же «столбик», определяя его ширину как , и суммируем их площади.
Для определения площади под графиком функции можно использовать следующий стохастический алгоритм:
Для малого числа измерений интегрируемой функции производительность Монте-Карло интегрирования гораздо ниже, чем производительность детерминированных методов. Тем не менее, в некоторых случаях, когда функция задана неявно, а необходимо определить область, заданную в виде сложных неравенств, стохастический метод может оказаться более предпочтительным.
При том же количестве случайных точек, точность вычислений можно увеличить, приблизив область, ограничивающую искомую функцию, к самой функции. Для этого необходимо использовать случайные величины с распределением, форма которого максимально близка к форме интегрируемой функции. На этом основан один из методов улучшения сходимости в вычислениях методом Монте-Карло: выборка по значимости.
Различные вариации метода Монте-Карло можно использовать для решения задач оптимизации. Например, алгоритм имитации отжига.
Компьютерное моделирование играет в современной физике важную роль и метод Монте-Карло является одним из самых распространенных во многих областях от квантовой физики до физики твердого тела, физики плазмы и астрофизики.
Традиционно метод Монте-Карло применялся для определения различных физических параметров систем, находящихся в состоянии термодинамического равновесия. Предположим, что имеется набор возможных состояний физической системы
. Для определения среднего значения
некоторой величины
необходимо рассчитать
, где суммирование производится по всем состояниям
из
,
— вероятность состояния
.
Прямое моделирование методом Монте-Карло какого-либо физического процесса подразумевает моделирование поведения отдельных элементарных частей физической системы. По сути это прямое моделирование близко к решению задачи из первых принципов, однако обычно для ускорения расчетов допускается применение каких-либо физических приближений. Примером могут служить расчеты различных процессов методом молекулярной динамики: с одной стороны система описывается через поведение ее элементарных составных частей, с другой стороны, используемый потенциал взаимодействия зачастую является эмпирическим.
Примеры прямого моделирования методом Монте-Карло:
Квантовый метод Монте-Карло широко применяется для исследования сложных молекул и твердых тел. Это название объединяет несколько разных методов. Первый из них это вариационный метод Монте-Карло, который по сути является численным интегрированием многомерных интегралов, возникающих при решении уравнения Шредингера. Для решения задачи, в которой участвует 1000 электронов, необходимо взятие 3000-мерных интегралов, и при решении таких задач метод Монте-Карло имеет огромное преимущество в производительности по сравнению с другими численными методами интегрирования. Другая разновидность метода Монте-Карло — это диффузионный метод Монте-Карло.
Другие примеры применения метода Монте-карло.
Математическое описание характеристик распространения света может быть выполнено аналитически с помощью уравнения теории Максвелла или через теории переноса. Применимость уравнений Максвелла ограничена из-за сложностей, связанных при выводе точных аналитических решений. С другой стороны, эвристический характер теории переноса позволяет использовать численные методы для решения перенос фотонов через поглощающие и рассеивающие среды. Метод Монте-Карло широко используется для решения задач радиационного передачи в связи с своей гибкости и простоте в моделировании переноса энергии в произвольных геометрий со сложными граничными условиями. Тем не менее, в большинстве моделирования не рассматривается поляризация света.
статистических методах моделирования переноса электронов в веществе.
Математическое моделирование процессов взаимодействия ионизирующего излучения с объектами сложной геометрии и внутренней структуры имеет большое значение во многих приложениях. В частности, в рамках задач рентгеновской диагностики материалов и конструкций требуется определить и исследовать рентгеновские изображения объектов , а при изучении электромагнитного воздействия проникающего излучения необходимо проанализировать распределение потоков релятивистских электронов, возникающих в результате взаимодействия ионизирующего излучения с материалами объектов. Вычислительные алгоритмы, основанные на статистическом моделировании методом Монте-Карло процессов переноса и взаимодействия излучения с веществом . Преимущество метода Монте-Карло перед альтернативными методами, основанными на численном решении кинетического уравнения, определяется удобством и приспособленностью этого метода к решению сложных граничных задач в многокомпонентных средах. Эффективность применения метода Монте-Карло определяется в настоящее время, вопервых, развитием способов уменьшения статистической погрешности результатов расчетов и, во-вторых, прогрессом в области создания быстродействующих многопроцессорных вычислительных систем. Статистическое моделирование переноса электронов и других заряженных частиц представляет значительно большую трудность, чем моделирование переноса фотонов.
Монте-Карло N-Particle Transport ( MCNP ) - это универсальный код переноса излучения Монте-Карло с непрерывной энергией, обобщенной геометрией, зависящий от времени, разработанный для отслеживания многих типов частиц в широком диапазоне энергий и разработанный Лос-Аламосская национальная лаборатория . Конкретные области применения включают, помимо прочего, радиационную защиту и дозиметрию, радиационную защиту , радиографию , медицинскую физику, безопасность ядерной критичности , проектирование и анализ детекторов, ядерный каротаж нефтяных скважин , проектирование мишеней ускорителей , деление иПроектирование, дезактивация и снятие с эксплуатации термоядерного реактора . Код обрабатывает произвольную трехмерную конфигурацию материалов в геометрических ячейках, ограниченных поверхностями первой и второй степени и эллиптическими торами четвертой степени.
Основной проблемой является генерация независимых случайных величин. Это не такая простая задача, как может показаться на первый взгляд. В примерах кода мы просто вызывали встроенные функции R или Python для генерации случайных чисел, но этот процесс может быть намного более сложным. При необходимости вы можете обратиться к научным источникам по данной теме.
Другая проблема состоит в том, как обеспечить сходимость ошибки. Обратите внимание на то, что в примере вычисления числа Пи ошибка перестала уменьшаться. В большинстве приложений метода Монте-Карло для решения этой проблемы используются очень большие выборки.
Напиши свое отношение про метод монте-карло. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое метод монте-карло и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы