Построение последовательности независимых действительных случайных величин кратко

Привет, мой друг, тебе интересно узнать все про построение последовательности независимых действительных случайных величин, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое построение последовательности независимых действительных случайных величин , настоятельно рекомендую прочитать все из категории вероятностные процессы.

построение последовательности независимых действительных случайных величин , имеющих заданные функции распределения.

Многие важные процессы удается строить, отправляясь от последовательности независимых случайных элементов.
Приведем ряд примеров такого рода. Отметим, что для построения последовательности независимых действительных случайных величин достаточно совершенно элементарных средств, как показывают упражнения 2 и 3.

Пример 1. Пусть 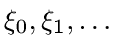— независимые случайные векторы, заданные на некотором вероятностном пространстве 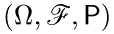и принимающие значения в пространстве 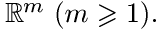. Случайный процесс (с дискретным временем)
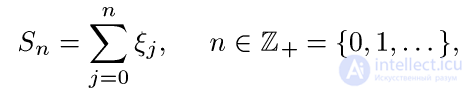, (9)

принято называть случайным блужданием.
Если представить себе частицу, которая в нулевой момент времени находится в точке 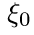и в каждый (дискретный) момент времени 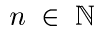смещается на
величину 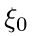, то тогда вектор (n,Sn) будет давать координаты этой частицы во времени и пространстве.

Пример 2. Для последовательности 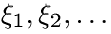независимых одинаково распределенных невырожденных неотрицательных случайных величин процесс восстановления определяется формулой

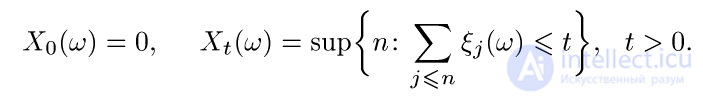
Всюду считаем сумму по пустому множеству равной нулю, поэтому 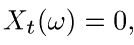, если 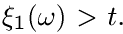. Вообще говоря, так определенные величины 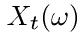принимают значения в 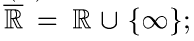; при этом σ-алгебра считается состоящей из множеств В и 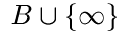, где .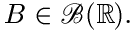
Название "процесс восстановления" объясняет следующая интерпретация. Пусть,
начиная с to = 0, в моменты, отделенные друг от друга промежутками 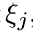происходят поломки некоторого устройства (например, перегорает электрическая лампочка), и вышедшее из строя устройство или его неисправный блок мгновенно заменяется идентичным новым. Тогда 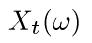есть число замен ("восстановлений") на промежутке (0, t]. Траекторию процесса 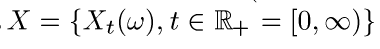дает рис. 2.

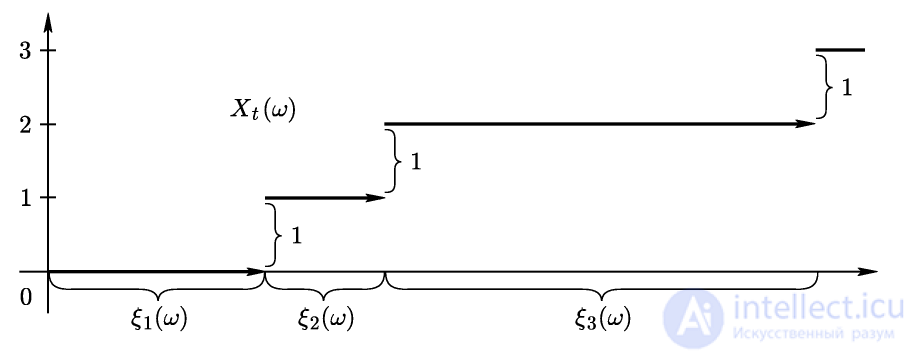
Рис. 2

Пример 3. Об этом говорит сайт https://intellect.icu . Рассмотрим на некотором вероятностном пространстве 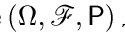две последовательности неотрицательных случайных величин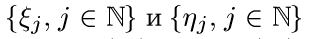
таких, что 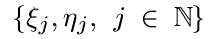независимы в совокупности и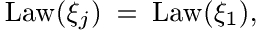

. Для положительных констант у0 и с определим процесс

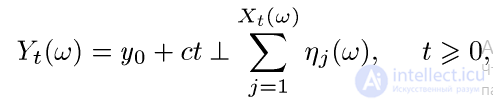
где 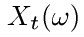задается формулой (10). Процессы вида (11) используются в модели страхования Крамера-Лундберга , в которой уо —
начальный капитал компании, с — скорость поступления взносов, 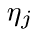— размер выплаты в случайный момент, a Yt интерпретируется как капитал компании в момент t.

Пример 4. Пусть 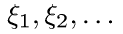— независимые одинаково распределенные случайные векторы, заданные на вероятностном пространстве 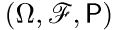и принимающие значения в .

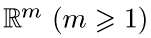Введем эмпирические меры

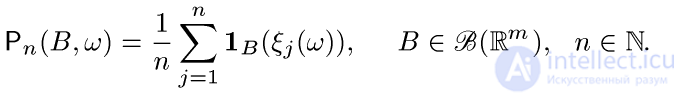(12)

Пользуясь определением 3, легко видеть, что формула (12) при каждом 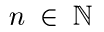задает случайный процесс, индексированный борелевскими множествами В, т.е.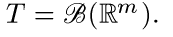
Вместо индикатора 1в в (12) можно было бы взять функцию f из некоторого класса 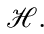. Тогда при должной измеримости f получится случайный процесс, индексированный семейством функций.

Пример 5. Пусть 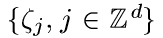— случайное поле, образованное независимыми одинаково распределенными векторами со значениями в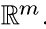 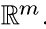Пусть μ есть σ-конечная мера* на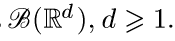

Определим процесс частных сумм

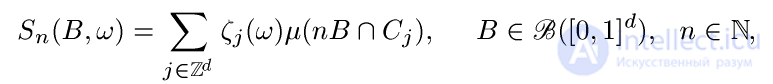(13)

где 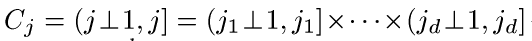- единичный куб с верхней вершиной
в точке .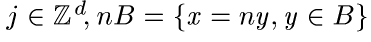
Другими словами, в отличие от (9) здесь берутся определенным образом взвешенные частные суммы.

примечание

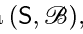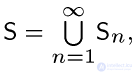*μ есть σ-конечная мера на если где 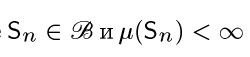для любого

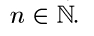
Пример 6. Пусть λ есть конечная мера (λ 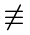0), заданная на некотором измеримом пространстве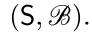

. Пусть Y, Х_1, Х₂,... — независимые случайные элементы на вероятностном пространстве 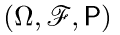такие, что Y — действительная пуассоновская величина с параметром 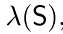, a X1, X2,... — независимые одинаково распределенные величины, являющиеся 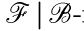измеримыми, для которых

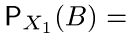
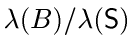при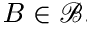

. Возможность такого построения вытекает из теоремы 2. (Обратите внимание, что здесь мы имеем дело с величинами Y и Хk со значениями в
разных пространствах.) Введем на 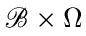функцию 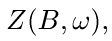положив

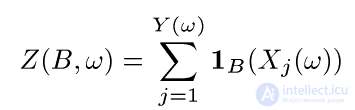(14)
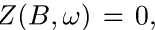( , когда 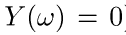). Формула (14) определяет так называемую пуассоновскую случайную меру с мерой интенсивности (или ведущей мерой) λ. Случай σ-конечной меры λ обсуждается в дополнении к этой главе.

Упражнение 2

Пусть — последовательность положительных чисел такая, что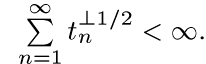

. Докажите, что тогда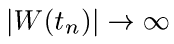 п.н. при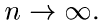


В дополнение к локальному закону повторного логарифма (см. следствие 3) сформулируем следующий полезный результат о локальном поведении траекторий винеровского процесса.

Упражнение 3. Рассмотрим последовательность 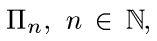, измельчающихся разбиений 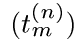отрезка [0, t] точками специального вида

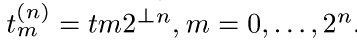
Тогда

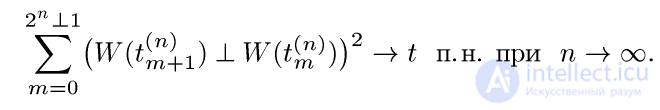
Перейдем непосредственно к описанию явной конструкции винеровского процесса (на отрезке [0,1]) с помощью последовательности независимых стандартных
гауссовских величин.

Теорема 8. Пусть 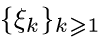— последовательность независимых случайных величин, имеющих стандартное нормальное распределение 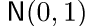и заданных на некотором вероятностном пространстве .

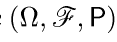Положим для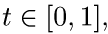

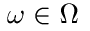
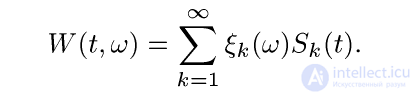
Тогда 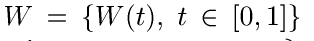есть винеровский процесс на [0,1], к тому же имеющий с вероятностью единица непрерывные траектории.

Основывные обозначения

Напиши свое отношение про построение последовательности независимых действительных случайных величин. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое построение последовательности независимых действительных случайных величин и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы

Из статьи мы узнали кратко, но содержательно про построение последовательности независимых действительных случайных величин