Фильтрация. Марковские моменты, момент остановки. Примеры

Привет, мой друг, тебе интересно узнать все про марковские моменты, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое марковские моменты, момент остановки , настоятельно рекомендую прочитать все из категории вероятностные процессы.

Марковский момент времени (в теории случайных процессов) — это случайная величина, не зависящая от будущего рассматриваемого случайного процесса.

Дискретный случай

Пусть дана последовательность случайных величин . Тогда случайная величина называется марковским моментом (времени), если для любого событие зависит только от случайных величин .

Пример

Пусть — последовательность независимых нормальных случайных величин. Пусть , и

— момент первого достижения процессом уровня . Тогда — марковский момент, ибо тогда и только тогда, когда существует такое, что . Таким образом событие зависит лишь от поведения процесса до момента времени .

Пусть теперь

— момент последнего достижения процессом уровня . Тогда не является марковским моментом, ибо событие предполагает знание поведения процесса в будущем.

Общий случай

• Пусть дано вероятностное пространство с фильтрацией , где . Тогда случайная величина принимающая значения в называется марковским моментом относительно данной фильтрации, если .

• Если дан процесс , и — его естественные σ-алгебры, то говорят, что — марковский момент относительно процесса .

• Марковский момент называется моментом остановки, если он конечен почти наверное, то есть

.

Свойства

Если и — марковские моменты , то

• — марковский момент;
• — марковский момент;
• — марковский момент.

Замечание: момент остановки может не иметь конечного математического ожидания.

Пример

Пусть — стандартный винеровский процесс. Пусть . Определим

.

Тогда — марковский момент, имеющий распределение, задаваемое плотностью вероятности

.

В частности — момент остановки. Однако,

.

Марковские моменты.

3.1. Определение. Пусть - случайная величина 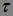называется марковским моментом, если 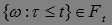для .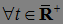

Конечный марковский момент называется моментом остановки (т. е. ).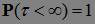

Пример. Пусть 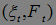непрерывен справа со значениями в 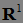тогда момент первого достижения уровня 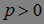: 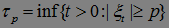, является марковским моментом.

Теорема 10. 1) Пусть 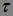- марковский момент, тогда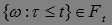
2) Пусть 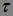- марковский момент, тогда .

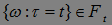Доказательство. 1) Так как 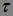- марковский момент, то 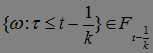. Отсюда при 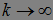получаем .

2) Так как 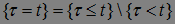, то из пункта 1) получаем утверждение. Доказательство закончено.

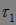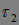Теорема 11. Если и - марковские моменты, то: 1) 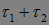- марковский момент, 2) 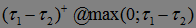- марковский момент.

Докажите самостоятельно.

3.2. Возникает естественный вопрос: при каких условиях случайная величина является марковским моментом?

Теорема 12. Случайная величина 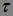- марковский момент, если 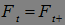для .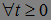

Доказательство. Так как 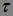- случайная величина, то 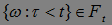. Об этом говорит сайт https://intellect.icu . Докажем, что 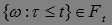. Из определения случайной величины следует, что Пересечем все эти множества, имеем , для 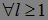. Поэтому в силу условий теоремы имеем 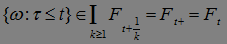.Доказательство закончено.

Теорема 13. Если есть два марковских момента, то 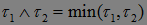и - марковские моменты.

Докажите самостоятельно.

3.3. Определение. Пусть — марковские моменты (м. м.), причем 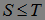Р - п. н.. Множества

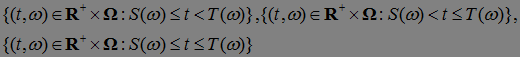
называются, соответственно, открытым справа, открытым слева, открытым справа и слева, за­мкнутым стохастическими интервалами и обозначаются, соответственно, через

Через 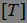обозначим множество 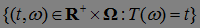и назовем его графиком марковского момента .

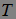Задача. Докажите, что .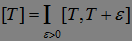

3.4. Определение. Случайное множество А называется тонким, если оно имеет вид , где 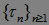- последовательность моментов остановки. Если, кроме того, последовательность 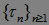такая, что 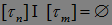при , то такую последовательность назовем исчерпывающей множество A.

Теорема 14. Тонкое множество А и все его 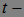сечения 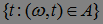не более чем счетны, кроме того, существует исчерпывающая последовательность моментов остановки.

3.5. Определение. Случайный процесс 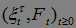называется остановленным если .

Определение. Пусть последовательность марковских моментов такая, что 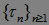, причем 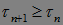Р -п. н. для 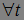и пусть
Р - п. н.. Такую последовательность назовем 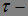локализующей (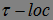). Если же , то последовательность 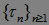назовем локализующей.

Определение. Случайный процесс 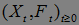называется 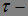локальным мартингалом , если существует 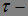локализующая последовательность 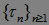марковских моментов такая, что для Р - п. н. .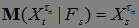

Аналогичным образом определяются локальные субмартингал и супермартингал.

Теорема 15. Пусть 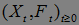- локальный мартингал относительно меры Р. Тогда 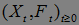- супермартингал (относительно меры Р).

Доказательство. Так как 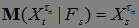Р — п.н. для , где 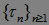- локализующая последовательность, то в силу леммы Фату .
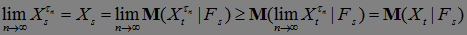Доказательство закончено.

3.6. Займемся теперь классификацией марковских моментов.

3.6.1. Определение. Марковский момент 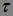называется предсказуемым, если существует последовательность марковских моментов 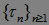такая, что: а) Р - п. н., б) 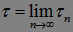Р - п. н., при этом последовательность 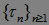называют предвещающей марковский момент .

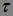Пример. Пусть момент остановки, а 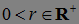. Ясно, что 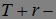момент остановки, более того 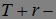предсказуемый момент остановки, так как 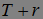предвещает последовательность 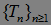, где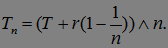

Определение. Марковский момент 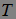называют достижимым, если существует предсказуемая последовательность 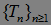марковских моментов таких, что Р - п. н., т. е.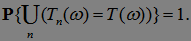

3.6.2. Определение. Марковский момент называется недостижимым (вполне или тотально недостижимым) или опциональным, если для каждого предсказуемого момента остановки 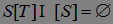Р - п. н. .

Задача. Докажите, что если марковский момент одновременно достижим и тотально не достижим, то 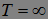Р - п. н..

Теорема 16. Марковский момент 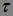- опционален тогда и только тогда, когда существует последовательность моментов остановки 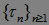такая, что: а) 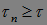Р - п. н. для , б) 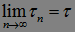Р - п. н..

Докажите самостоятельно.

Очевидно следующее утверждение.

Теорема 17. Пусть 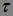— опциональный марковский момент. Тогда для любой предсказуемой последовательности марковских моментов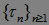

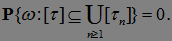
Задача. Докажите, что момент времени в который происходит первый скачок пуассоновского процесса 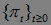является опциональным марковским моментом.

Теорема 18. Пусть 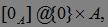где 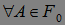, и стохастические интервал вида 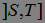, где - опциональные марковские моменты, порождают алгебру .

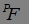Доказательство. Сначала заметим, что 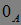- это предсказуемый момент остановки равный нулю на и бесконечности на 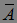. Значит 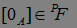. Очевидно, что 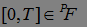. Заметим, что 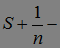предсказуемым м. о., поэтому 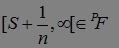, следовательно .

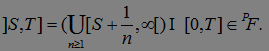Рассмотрим интервал 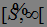, где - предсказуемый м.о. Нам надо показать, что этот интервал принадлежит алгебре порожденной выше рассмотренными интервалами. Действительно, поскольку 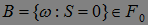, а для последовательностей , предвещающей на множестве 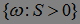, имеем 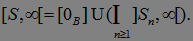Отсюда следует утверждение теоремы.

Примеры и применение

Чтобы проиллюстрировать некоторые примеры случайных моментов, когда правила останавливаются, а некоторые - нет, рассмотрим игрока, играющего в рулетку с типичным преимуществом казино, начиная со 100 долларов и делая ставку 1 доллар на красное в каждой игре:

• Ровно пять игр соответствуют времени остановки τ = 5 и являются правилом остановки.
• Играть, пока у него не закончатся деньги или не сыграет 500 игр, является правилом остановки.
• Игра до тех пор, пока он не наберет максимальное количество очков впереди, не является правилом остановки и не предусматривает время остановки, поскольку требует информации о будущем, а также о настоящем и прошлом.
• Игра до тех пор, пока он не удвоит свои деньги (занимая при необходимости) , не является правилом остановки, поскольку существует положительная вероятность того, что он никогда не удвоит свои деньги.
• Игра до тех пор, пока он не удвоит свои деньги или не закончатся деньги, является правилом остановки, даже если потенциально нет ограничения на количество игр, которые он играет, поскольку вероятность того, что он остановится через конечное время, равна 1.

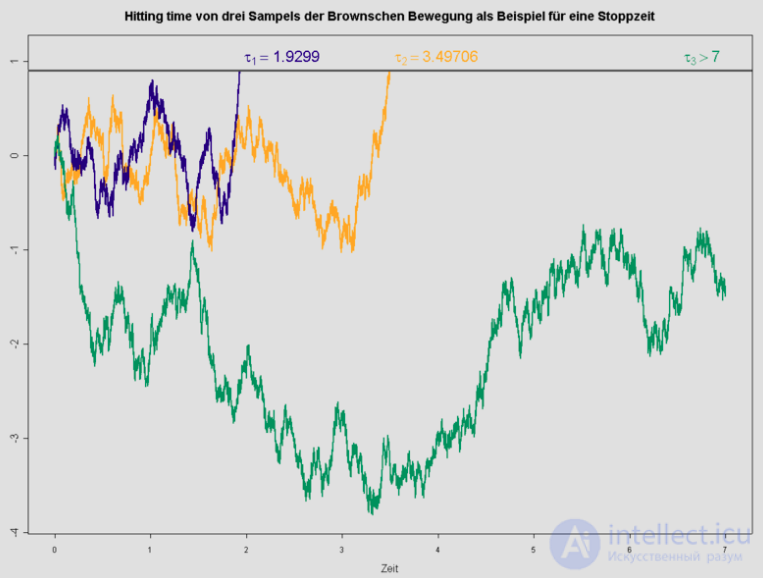
Чтобы проиллюстрировать более общее определение остановки времени, рассмотрим броуновское движение , которое является случайным процессом., где каждый - случайная величина, определенная на вероятностном пространстве . Мы определяем фильтрацию на этом вероятностном пространстве, позволяя- σ -алгебра, порожденная всеми множествами вида куда и - борелевское множество . Интуитивно понятно, что событие E находится втогда и только тогда, когда мы можем определить, истинно или ложно E, просто наблюдая за броуновским движением от времени 0 до момента t .

• Каждая константа (тривиально) время остановки; это соответствует правилу остановки "остановить вовремя".
• Позволять потом - время остановки для броуновского движения, соответствующее правилу остановки: «остановитесь, как только броуновское движение превысит значение a ».
• Другое время остановки задается . Это соответствует правилу остановки: «остановитесь, как только броуновское движение станет положительным на непрерывном участке длиной 1 единицу времени».
• В общем, если τ ₁ и τ ₂ являются временами остановки на тогда их минимум , их максимум , и их сумма τ ₁ + τ ₂ также являются моментами остановки. (Это неверно для различий и продуктов, потому что они могут потребовать «заглянуть в будущее», чтобы определить, когда остановиться.)

Время попадания, подобное приведенному выше второму примеру, может быть важным примером времени остановки. Хотя относительно просто показать, что, по существу, все времена остановки - это времена попадания ^, может быть намного сложнее показать, что определенное время достижения является временем остановки. Последние типы результатов известны как теорема Дебю .

Типы времени остановки

Моменты остановки с установленным индексом времени I = [0, ∞) часто делятся на один из нескольких типов в зависимости от того, можно ли предсказать, когда они вот-вот произойдут.

Время остановки τ является предсказуемым , если она равна пределом возрастающей последовательности моментов остановки т _п , удовлетворяющий т _п < т , когда τ > 0. Последовательности τ _п называется объявить τ и предсказуемые времена остановочных иногда называют анонсируемый . Примерами прогнозируемого времени остановки являются время срабатывания непрерывных и адаптированных процессов. Если τ - это первый раз, когда непрерывный и вещественнозначный процесс X равен некоторому значению a, то это объявляется последовательностью τ _n , где τ _n - это первый момент, когда X находится на расстоянии 1 / n от a .

Доступное время остановки - это время, которое может быть покрыто последовательностью предсказуемых времен. То есть время остановки τ доступно, если P ( τ = τ _n для некоторого n ) = 1, где τ _n - предсказуемые времена.

Стопорное время τ является абсолютно недоступным , если она никогда не может быть объявлена возрастающей последовательностью времени остановки. Эквивалентно, P ( τ = σ <∞) = 0 для каждого предсказуемого времени σ . Примеры полностью недоступных времен остановки включают времена скачков пуассоновских процессов .

Каждый момент остановки τ можно однозначно разложить на доступное и полностью недоступное время. То есть существует единственный доступный момент остановки σ и полностью недоступный момент υ такие, что τ = σ, если σ <∞, τ = υ, если υ <∞, и τ = ∞, если σ = υ = ∞. Обратите внимание, что в формулировке этого результата разложения времена остановки не обязательно должны быть почти наверняка конечными и могут равняться ∞.

Правила остановки в клинических испытаниях

Клинические испытания в медицине часто проводят промежуточный анализ, чтобы определить, достигли ли испытания уже своих конечных точек. Однако промежуточный анализ создает риск ложноположительных результатов, и поэтому границы остановки используются для определения количества и времени промежуточного анализа (также известного как альфа-расход, чтобы обозначить частоту ложноположительных результатов). В каждом из R промежуточных тестов испытание останавливается, если вероятность ниже порогового значения p, которое зависит от используемого метода.

Задачи для самостоятельного решения

1. Пусть задана фильтрация 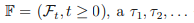— марковские моменты относительно F.

Докажите, что

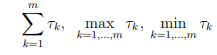
тоже являются марковскими моментами относительно F.

2. Дана фильтрация 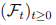и марковские моменты τ и σ относительно нее. Для τ определим сигма-алгебру

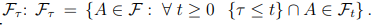. Докажите, что если

Вау!! 😲 Ты еще не читал? Это зря!

• Оптимальная остановка
• Алгоритм коэффициентов
• Проблема секретаря
• Время попадания
• Остановленный процесс
• Проблема расстройства
• Теорема Дебю
• Последовательный анализ

Напиши свое отношение про марковские моменты. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое марковские моменты, момент остановки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы