2.10. Некоторые полезные оценки для функций восстановления кратко

Привет, Вы узнаете о том , что такое полезные оценки для функций восстановления , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое полезные оценки для функций восстановления , настоятельно рекомендую прочитать все из категории вероятностные процессы.

2.10. Некоторые полезные оценки для функций восстановления

Часто возникает необходимость оценивать поведение функции восстановления H(t) при конечном значении аргумента t. Для этого приведем некоторые полезные оценки для функции восстановления на любом конечном интервале времени. Основой получения этих оценок служит равенство (2.4) для функции восстановления и аналогичное равенство для плотности восстановления.

1. Функция восстановления.

Для функции восстановления из (2.4) следует очевидное неравенство F(t)<=H(t). Для получения оценки сверху заметим, что поскольку ξ_k>=0 и справедливо следующее соотношение между событиями

{max_{k=(1,2,...,n)}ξ_k⊇{t_n

и, следовательно, справедливо неравенство

F⁽ⁿ⁾(t)=P(t_n<=P{max_{k=(1,2,...,n)}ξ_kⁿ(t),

так как случайные величины ξ_k независимы. Поэтому из (2.4) получаем двустороннюю оценку

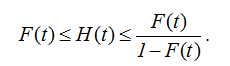. (2.54)

Оценку (2.54) можно уточнить. Об этом говорит сайт https://intellect.icu . Воспользуемся для этого очевидным равенством

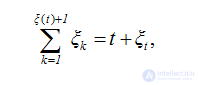
где по-прежнему обозначены ξ(t) число восстановлений, произошедших до момента времени t, ξ_t - прямое время возвращения (время перескока).

Если использовать тождество Вальда (математическое приложение 5), то получаем

M(ξ₁+ξ₂+...+ξ_ξ(t)+1)=Mξ (Mξ(t)+1)= Mξ[H(t)+1]=t+Mξ_t,

поскольку случайные величины ξ_i одинаково распределены и при i>ξ(t)+1 не зависят от ξ(t) по определению процесса восстановления.

Следовательно,

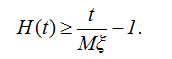. (2.55)

Объединяя неравенства (2.54) и (2.55), получаем

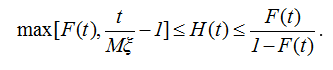. (2.56)

2. Плотность восстановления.

Для производной свертки справедлива оценка при n>1

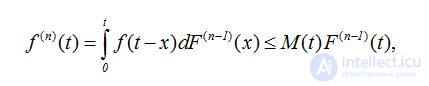
где обозначено .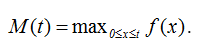

Тогда из равенства для плотности восстановления 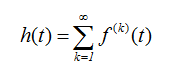получаем следующие оценки

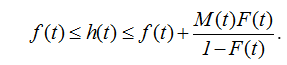. (2.57)

3. Сравнение функций восстановления.

Свойство, о котором пойдет речь, можно назвать свойством монотонной зависимости функции восстановления от функции распределения, соответствующей ей.

Итак, пусть заданы два простых процесса восстановления, для которых интервалы между восстановлениями имеют распределения F(x) и G(x) соответственно. Обозначим через H_F(x) и H_G(x) их функции восстановления. Тогда справедлива следующая

ЛЕММА 2.3. Если при x>=0 справедливо неравенство F(x)>=G(x), то

H_F(x)>=H_G(x). (2.58)

ДОКАЗАТЕЛЬСТВО. Используя метод математической индукции, докажем неравенство F⁽ⁿ⁾(x)>=G⁽ⁿ⁾(x), n>0. В самом деле, коль скоро F⁽¹⁾(x)=F(x) и G⁽¹⁾(x)=G(x), то по условию леммы неравенство справедливо для n=1. Предположим, что оно верно для произвольного n>1. Докажем справедливость этого неравенства для n+1 . Из определения интеграла свертки получаем

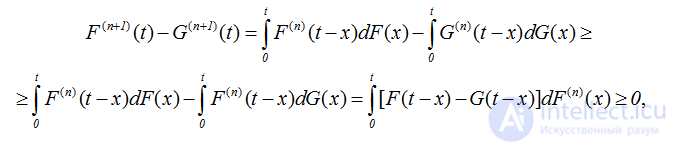
что и доказывает утверждение леммы, если воспользоваться равенством (2.4) для функции восстановления. *

Вау!! 😲 Ты еще не читал? Это зря!

• Случайная мера Пуассона
• случайный процесс
• случайные блуждания
• процесс восстановления
• модель Крамера-Лундберга
• эмпирические меры
• пуассоновская случайная мера

Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области полезные оценки для функций восстановления имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое полезные оценки для функций восстановления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы

Из статьи мы узнали кратко, но содержательно про полезные оценки для функций восстановления