Спектральная плотность. Процесс скользящего среднего как процесс, обладающий спектральной плотностью. кратко

Привет, мой друг, тебе интересно узнать все про спектральная плотность, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое спектральная плотность, процесс скользящего среднего как процесс обладающий спектральной плотностью , настоятельно рекомендую прочитать все из категории вероятностные процессы.

В статистической радиотехнике и физике при изучении детерминированных сигналов и случайных процессов широко используется их спектральное представление в виде спектральной плотности, которая базируется на преобразовании Фурье.

Если процесс имеет конечную энергию и квадратично интегрируем (а это нестационарный процесс), то для одной реализации процесса можно определить преобразование Фурье как случайную комплексную функцию частоты:

(1)

Однако она оказывается почти бесполезной для описания ансамбля. Выходом из этой ситуации является отбрасывание некоторых параметров спектра, а именно спектра фаз, и построении функции, характеризующей распределение энергии процесса по оси частот. Тогда согласно теореме Парсеваля энергия

(2)

Функция характеризует, таким образом, распределение энергии реализации по оси частот и называется спектральной плотностью реализации. Усреднив эту функцию по всем реализациям можно получить спектральную плотность процесса.

Перейдем теперь к стационарному в широком смысле центрированному случайному процессу {\displaystyle x(t)}, реализации которого с вероятностью 1 имеют бесконечную энергию и, следовательно, не имеют преобразования Фурье. спектральная плотность мощности такого процесса может быть найдена на основании теоремы Винера-Хинчина как преобразование Фурье от корреляционной функции:

(3)

Если существует прямое преобразование, то существует и обратное преобразование Фурье, которое по известной определяет :

(4)

Если полагать в формулах (3) и (4) соответственно и , имеем

(5)

(6)

Формула (6) с учетом (2) показывает, что дисперсия определяет полную энергию стационарного случайного процесса, которая равна площади под кривой спектральной плотности. Размерную величину можно трактовать как долю энергии, сосредоточенную в малом интервале частот от {\displaystyle f-df/2} до . Если понимать под {\displaystyle x(t)} случайный (флуктуационный) ток или напряжение, то величина {\displaystyle S_{x}(f)} будет иметь размерность энергии [В2/Гц] = [В2с]. Поэтому иногда называют энергетическим спектром. В литературе часто можно встретить другую интерпретацию: – рассматривается как средняя мощность, выделяемая током или напряжением на сопротивлении 1 Ом. При этом величину называют спектром мощности случайного процесса.

Свойства спектральной плотности

• Энергетический спектр стационарного процесса (вещественного или комплексного) – неотрицательная величина:

.

(7)

• Энергетический спектр вещественного стационарного в широком смысле случайного процесса есть действительная и четная функция частоты:

.

(8)

• Корреляционная функция и энергетический спектр стационарного в широком смысле случайного процесса обладают всеми свойствами, характерными для пары взаимных преобразований Фурье. В частности, чем «шире» спектр тем «уже» корреляционная функция , и наоборот. Этот результат количественно выражается в виде принципа или соотношения неопределенности.

Процессы скользящего среднего

Предположим, что 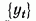процесс скользящего среднего некоррелированных случайных величин

где 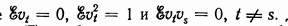Для сходимости в среднем ряда (7) необходимо и достаточно, чтобы

(следствие 7.6.1). Об этом говорит сайт https://intellect.icu . Процесс имеет спектральную плотность, равную а спектральной плотностью процесса является

Процесс называется процессом скользящего среднего. Ковариационной функцией для является величина

так как если и равно 0 в остальных случаях.

Обратно, если стационарный процесс имет спектральную плотность его можно представить в виде (7). Квадратный корень из можно представить следующим образом:

где Так как четная функция, то вещественные. [Заметим, что в том случае, когда не выполняется, определяется (7), является комплексной величиной.] Существует последовательность некоррелированных случайных величин такая, что могут быть представлены как

Определим используя спектральное представление процесса Предположим, Пусть

Тогда

так как

ввиду Таким образом, из формулы (12) получаем требуемое равенство. Более подробное изложение см. в книге Дуба (1953, гл. X, разд. 8).

Если имеет спектральную плотность почти везде на и

то существуют (действительные) постоянные и последовательность случайных величин такие, что

Сумма (16), вообще говоря, бесконечна (см. разд. 7.6.3).

Теперь рассмотрим процесс скользящего среднего с конечными лределами суммирования

где Тогда

где 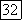корни уравнения

Если то все корней отличны от нуля. Для конечного 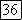будем использовать как стандартную форму в Как было показано в разд. 5.7.1, любой процесс с конечным числом отличных от нуля ковариаций имеет ту же самую последовательность ковариаций, как выбранный соответствующим образом конечный процесс скользящего среднего. Тогда спектральную плотность можно записать в виде (18). Если

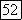Так как к монотонно изменяется от —1 до 1 на отрезке и от 1 до —1 на отрезке то функция возрастает от до на отрезке и убывает до на отрезке для если же то убывает на отрезке и возрастает на Таким образом, если то большую плотность имеют нижние частоты, - если 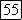верхние. Ввиду того что 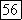спектральную

плотность можно записать следующим образом:

Последняя форма соответствует процессу имеет дисперсию Ковариационные функции этого процесса и процесса, определенного формулой (20), совпадают. Если , то последний процесс скользящего среднего отличается от предыдущего. [Спектральную плотность, соответствующую можно записать в виде где имеет дисперсию .]

Если

Если то 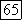есть максимум функции минимум; если то 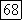минимум, 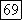максимум. Если то для значения X на отрезке и в точке если (подразумевая, что и корни соответствующего полинома комплексны), то есть минимум, а -относительный максимум; если (подразумевая, что и корни действительны), то есть максимум, а относительный минимум. Если 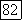корни уравнения

то

Так как 1, то множитель можно заменить на где 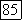сопряжено с 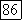можно заменить на Таким образом, для функции верно любое из следующих выражений:

Если действительны, то каждое из приведенных выражений соответствует спектральной плотности процесса скользящего среднего. Четыре процесса скользящего среднего различны, если три процесса скользящего среднего различны, если два процесса скользящего среднего различны, если или если наконец, существует только один процесс скользящего среднего, если Спектральная плотность является произведением двух плотностей указанного типа для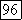

Если комплексно сопряжены, скажем 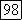то не действительны, если 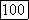и первые два выражения функции 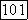в (27) не могут 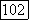соответствовать процессу скользящего среднего с действительными коэффициентами. Два процесса скользящего среднего с действительными коэффициентами различны. Все выражения для 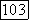и процессы скользящего среднего совпадают, если 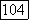(т. е. 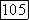Когда корни комплексно сопряжены,

Если у близко к 1, то минимальное значение 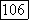достигается для значений X, близких ±0. Действительно, минимум функции (28) достигается при если последнее выражение меньше 1 по абсолютной величине.

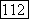Для произвольного спектральная плотность есть произведение, аналогичное формулам (21) и (28). Пусть (Если то Для некоторых Тогда

Если 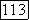близко к 1 (т. е. если 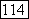лежит близко к единичному кругу в комплексной плоскости), то

будет близко к 0. Таким образом, частоты вблизи 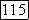будут иметь малую интенсивность.

В общем случае множитель 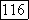как показано в формуле (18), можно переписать так:

где 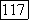комплексно сопряжено 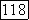Если все корни действительны, различны и отличны от ±1, то существует 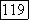различных представлений функции 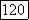соответствующих различным процессам скользящего среднего. Число различных процессов скользящего среднего в общем случае зависит от числа корней, абсолютные значения которых равны 1, а также от кратности различных корней и числа комплексно сопряженных корней. Мы не будем перечислять все возможности для случая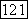

Нам будет удобно представить процесс скользящего среднего в таком виде, чтобы ни один корень формулы (19) не был больше единицы по абсолютной величине. (Заметим, что корень, абсолютное значение которого есть 1, допускается для процесса скользящего среднего.)

Процесс скользящего среднего (17) можно записать в виде

где операторы и 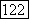определены так, что 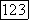Если корни в (19) меньше 1 по абсолютной величине, то из (32) следует

Если

то (33) перепишем в виде

или

Таким образом,

является наилучшим прогнозом величин 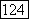по значениям 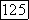в том смысле, что минимизируется среднеквадратичная ошибка.

Вау!! 😲 Ты еще не читал? Это зря!

• Преобразование Фурье
• Теорема Парсеваля
• Теорема Хинчина-Колмогорова
• База сигнала
• Спектральная плотность мощности
• Спектральная плотность излучения

Я хотел бы услышать твое мнение про спектральная плотность Надеюсь, что теперь ты понял что такое спектральная плотность, процесс скользящего среднего как процесс обладающий спектральной плотностью и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы

Из статьи мы узнали кратко, но содержательно про спектральная плотность