Лекция
Привет, мой друг, тебе интересно узнать все про случайные элементы, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое случайные элементы, распределения случайные элементов, случайный процесс как семейство случайных элементов, случайный процесс , настоятельно рекомендую прочитать все из категории вероятностные процессы.
случайные элементы и их распределения. случайный процесс как семейство случайных элементов и как одно измеримое отображение.
Случайный процесс (вероятностный процесс, случайная функция, стохастический процесс) в теории вероятностей — семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты.
Пусть — измеримое пространство,
множество значений параметра
. Функция
параметра
, значениями которой являются случайные величины
на пространстве элементарных событий
в фазовом пространстве
, называется случайным процессом в фазовом пространстве
.
Случайный элемент это функция
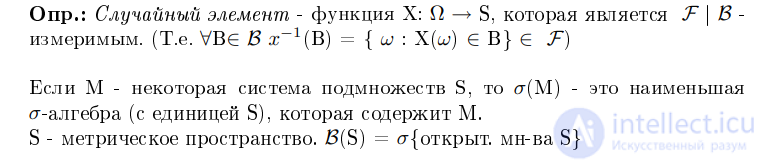
Используемые в области исследований и прикладного применения случайных процессов классификация и терминология являются нестрогими. В частности, термин «случайный процесс» часто используется как безусловный синоним термина «случайная функция».В зависимости от вида множества часто применяются следующие термины.
Всевозможные совместные распределения вероятностей значений :
называются конечномерными распределениями вероятностей случайного процесса .
Случайные процессы и
, принимающие значение в фазовом пространстве
называется эквивалентными, если при любом
эквивалентны соответствующие значения
и
.
При каждом фиксированном функция
параметра
со значениями в фазовом пространстве
называется реализацией или траекто́рией случайного процесса
. Об этом говорит сайт https://intellect.icu . Случайный процесс
называется непосредственно заданным, если каждый элементарный исход описывается соответствующей траекторией
в функциональном пространстве
всех функций на множестве
со значениями в фазовом пространстве
; точнее, если
и
— алгебра
порождается всевозможными цилиндрическими множествами
, где
и
, а значения
имеют вид
,
. Любому случайному процессу можно поставить в соответствие непосредственно заданный случайный процесс с теми же самыми конечномерный распределениями. Для каждого согласованного семейства конечномерных распределений вероятностей
(
таких, что
, являются плотными мерами в фазовом топологическом пространстве
, существует непосредственно заданный случайный процесс
с такими же конечномерными распределениями вероятностей.
Ковариационная функция. Пусть действительный или комплексный случайный процесс на множестве
, имеющий вторые моменты:
. Значения случайного процесса
можно рассматривать как элементы гильбертова пространства
— пространства всех случайных величин
,
, со скалярным произведением
.
Важнейшими характеристиками такого случайного процесса являются его математическое ожидание
и ковариационная функция
.
Вместо ковариационной функции может применятся корреляционная функция , являющуюся ковариационной функцией процесса
с нулевым математическим ожиданием.
При равенстве аргументов () корреляционная функция равна дисперсии случайного процесса
.
Функция двух переменных
и
является ковариационной функцией некоторого случайного процесса
,
, тогда и только тогда, когда она для всех
удовлетворяет следующему условию положительной определенности:
для любых и любых комплексных чисел
.
является случайным процессом.
Напиши свое отношение про случайные элементы. Это меня вдохновит писать для тебя всё больше и больше интересного. Спасибо Надеюсь, что теперь ты понял что такое случайные элементы, распределения случайные элементов, случайный процесс как семейство случайных элементов, случайный процесс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Из статьи мы узнали кратко, но содержательно про случайные элементы
Комментарии
Оставить комментарий
вероятностные процессы
Термины: вероятностные процессы