Лекция
Привет, Вы узнаете о том , что такое обрывающиеся процессы восстановления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое обрывающиеся процессы восстановления , настоятельно рекомендую прочитать все из категории вероятностные процессы.
До сих пор ограничениями были:
При этих условиях процесс восстановления будет развиваться во времени, за конечное время произойдет конечное число восстановлений (не будет бесконечных накоплений), а за бесконечное время произойдет бесконечное число восстановлений, то есть при t→∞ с вероятностью единица ξ(t)→∞.
Такая ситуация имеет место, когда распределение, определяющее процесс восстановления, является собственным, то есть P{ξ<∞}=limt→∞F(t)=F(∞)=1 (условие, необходимое для существования моментов).
Другая картина возникает в случае, когда распределение F(t) является несобственным, F(∞)<1, P{ξ=∞}=1-F(∞)>0. Тогда с положительной вероятностью 1-F(∞)>0 процесс восстановления может оборваться на каком-то шаге, то есть время до следующего восстановления будет равно бесконечности.
Процесс восстановления, у которого распределение интервалов между соседними моментами восстановления является несобственным, называется обрывающимся процессом восстановления.
Прежде чем формулировать теорему о предельном поведении обрывающегося процесса восстановления, докажем лемму о предельном поведении интегралов свертки.
ЛЕММА 2.2. Если функции А(x) и В(x) при x>0 положительные неубывающие и равномерно ограниченные, то
ДОКАЗАТЕЛЬСТВО. Об этом говорит сайт https://intellect.icu . В силу условий теоремы для любого ε1>0 найдется такое t1(ε1)>0, что при t>t1(ε1)
.
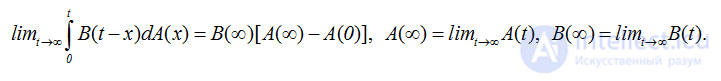
Для любого ε2>0 найдется такое t2(ε2)>0, что при t>t2(ε2) и
.
Тогда при t>max[t1(ε1), t2(ε2)] имеем оценку
что и доказывает утверждение леммы. *
ТЕОРЕМА 2.2. Для обрывающегося процесса восстановления, начинающегося в момент t=0, справедливы следующие утверждения:
; 
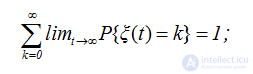(2.24)
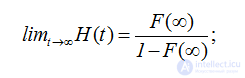(2.25)
. 
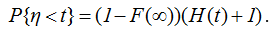(2.26)
ДОКАЗАТЕЛЬСТВО. Для несобственного распределения непосредственный переход к пределу при t→∞ в интеграле свертки дает F(k)(∞)=[F(∞)]k<1, k>0, и F(0)(∞)<1. Доказательство этого факта легко провести по индукции, используя лемму 2.2. Функции распределения удовлетворяют условиям леммы. Поэтому . Если , то из утверждения леммы следует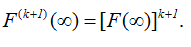 
Тогда из (2.3) получаем
P{ξ(∞)=k}=limt→∞ P{ξ(t)=k}=limt→∞ [F(k)(t)-F(k+1)(t)]=(F(∞))k[1-F(∞)] (2.27)
и, следовательно, справедливо (2.24).
Для доказательства (2.25) воспользуемся равенством (2.4)
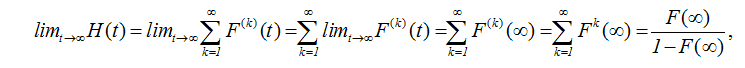
причем перемена порядка суммирования и перехода к пределу законна, поскольку ряд (2.4) сходится равномерно при 0<=t<∞.
Равенство (2.27) показывает, что число слагаемых ξm до обрыва процесса восстановления имеет геометрическое распределение. Тогда по формуле полной вероятности получаем
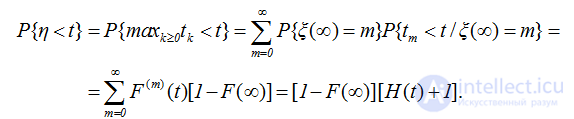
При вычислении условной вероятности ,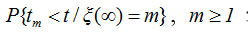 
заметим, что справедливо равенство событий
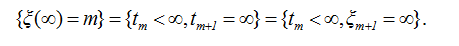
Поэтому в силу независимости случайных величин ξm+1 и tm имеем
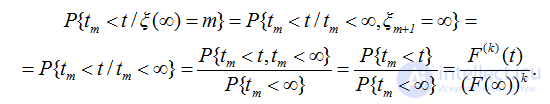
Таким образом, все утверждения теоремы доказаны. *
СЛЕДСТВИЕ 2.1. Если неубывающая функция В(x) имеет предел при x→∞, B(∞)=limx→∞B(x) и H(x) функция восстановления обрывающегося процесса восстановления, то
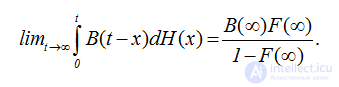
ДОКАЗАТЕЛЬСТВО. Доказательство непосредственно вытекает из равенства (2.25) и утверждения леммы 2.2.*
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области обрывающиеся процессы восстановления имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое обрывающиеся процессы восстановления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории вероятностные процессы
Из статьи мы узнали кратко, но содержательно про обрывающиеся процессы восстановления
Комментарии