Лекция
Привет, Вы узнаете о том , что такое следствия закона больших чисел, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое следствия закона больших чисел, теоремы бернулли, пуассона , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Известная теорема Я. Бернулли, устанавливающая связь между частотой события и его вероятностью, может быть доказана как прямое следствие закона больших чисел.
Пусть производится  независимых опытов, в каждом из которых может появиться или не появиться некоторое событие
независимых опытов, в каждом из которых может появиться или не появиться некоторое событие 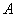 , вероятность которого в каждом опыте равна
, вероятность которого в каждом опыте равна 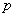 . Теорема Я. Бернулли утверждает, что при неограниченном увеличении числа опытов
. Теорема Я. Бернулли утверждает, что при неограниченном увеличении числа опытов  частота события
частота события 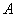 сходится по вероятности к его вероятности
сходится по вероятности к его вероятности 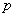 .
.
Обозначим частоту события 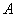 в
в  опытах через
опытах через 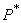 и запишем теорему Я. Бернулли в виде формулы
и запишем теорему Я. Бернулли в виде формулы
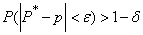 , (13.5.1)
, (13.5.1)
где, 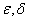 - сколь угодно малые положительные числа.
- сколь угодно малые положительные числа.
Требуется доказать справедливость этой формулы при достаточно большом  .
.
Доказательство. Рассмотрим независимые случайные величины:
 - число появлений события
- число появлений события 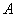 в первом опыте;
в первом опыте;
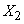 - число появлений события
- число появлений события 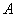 во втором опыте, и т. Об этом говорит сайт https://intellect.icu . д.
во втором опыте, и т. Об этом говорит сайт https://intellect.icu . д.
Все эти величины прерывны и имеют один и тот же закон распределения, выражаемый рядом вида:
|
|
|
|
|
|
где 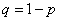 . Математическое ожидание каждой из величин
. Математическое ожидание каждой из величин 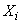 равно
равно 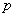 , а ее дисперсия
, а ее дисперсия 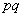 (см.
(см.  10.3).
10.3).
Частота 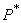 представляет собой не что иное, как среднее арифметическое величин
представляет собой не что иное, как среднее арифметическое величин 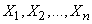 :
:
 ,
,
и, согласно закону больших чисел, сходится по вероятности к общему математическому ожиданию этих случайных величин. Отсюда и следует справедливость неравенства (13.5.1).
Теорема Я. Бернулли утверждает устойчивость частоты при постоянных условиях опыта. Но при изменяющихся условиях опыта аналогичная устойчивость также существует. Теорема, устанавливающая свойство устойчивости частот при переменных условиях опыта, называется теоремой пуассона и формулируется следующим образом:
Если производится  независимых опытов и вероятность появления события
независимых опытов и вероятность появления события 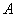 в
в  -м опыте равна
-м опыте равна 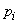 , то при увеличении
, то при увеличении  частота события
частота события 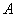 сходится по вероятности к среднему арифметическому вероятностей
сходится по вероятности к среднему арифметическому вероятностей 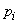 .
.
Теорема Пуассона выводится из обобщенной теоремы Чебышева точно так же, как теорема Бернулли была выведена из закона больших чисел.
Теорема Пуассона имеет большое принципиальное значение для практического применения теории вероятностей. Дело в том, что зачастую вероятностные методы применяются для исследования явлений, которые в одних и тех же условиях не имеют шансов повториться достаточно много раз, но повторяются многократно при весьма разнообразных условиях, причем вероятности интересующих нас событий сильно зависят от этих условий. Например, вероятность поражения цели в воздушном бою существенно зависит от дальности стрельбы, ракурса цели, высоты полета, скорости стреляющего самолета и цели и т. д. Комплекс этих условий слишком многочислен для того, чтобы можно было рассчитывать на многократное осуществление воздушного боя именно в данных фиксированных условиях. И все же, несмотря на это, в данном явлении налицо определенная устойчивость частот, а именно частота поражения цели в реальных воздушных боях, осуществляемых в самых разных условиях, будет приближаться к средней вероятности поражения цели, характерной для данной группы условий. Поэтому те методы организации стрельбы, которые основаны на максимальной вероятности поражения цели, будут оправданы и в данном случае, несмотря на то, что нельзя ожидать подлинной массовости опытов в каждом определенном комплексе условий.
Аналогичным образом обстоит дело в области опытной проверки вероятностных расчетов. На практике очень часто встречается случай, когда требуется проверить на опыте соответствие вычисленной вероятности какого-либо события 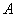 его фактической частоте. Чаще всего это делается для того, чтобы проверить правильность той или иной теоретической схемы, положенной в основу метода вычисления вероятности события. Зачастую при такой экспериментальной проверке не удается воспроизвести достаточно много раз одни и те же условия опыта. И все же эта проверка может быть осуществлена, если сравнить наблюденную в опыте частоту события не с его вероятностью для фиксированных условий, а со средним арифметическим вероятностей, вычисленных для различных условий.
его фактической частоте. Чаще всего это делается для того, чтобы проверить правильность той или иной теоретической схемы, положенной в основу метода вычисления вероятности события. Зачастую при такой экспериментальной проверке не удается воспроизвести достаточно много раз одни и те же условия опыта. И все же эта проверка может быть осуществлена, если сравнить наблюденную в опыте частоту события не с его вероятностью для фиксированных условий, а со средним арифметическим вероятностей, вычисленных для различных условий.
Информация, изложенная в данной статье про следствия закона больших чисел , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое следствия закона больших чисел, теоремы бернулли, пуассона и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про следствия закона больших чисел
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ