10.2. Теоремы о числовых характеристиках

Привет, Вы узнаете о том , что такое теоремы о числовых характеристиках, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теоремы о числовых характеристиках , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В предыдущем 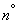 мы привели ряд формул, позволяющих находить числовые характеристики функций, когда известны законы распределения аргументов. Однако во многих случаях для нахождения числовых характеристик функций не требуется знать даже законов распределения аргументов, а достаточно знать только некоторые их числовые характеристики; при этом мы вообще обходимся без каких бы то ни было законов распределения. Определение числовых характеристик функций по заданным числовым характеристикам аргументов широко применяется в теории вероятностей и позволяет значительно упрощать решение ряда задач. По преимуществу такие упрощенные методы относятся к линейным функциям; однако некоторые элементарные нелинейные функции также допускают подобный подход.

 

В настоящем 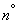 мы изложим ряд теорем о числовых характеристиках функций, представляющих в своей совокупности весьма простой аппарат вычисления этих характеристик, применимый в широком круге условий.

 

1. Математическое ожидание неслучайной величины

 

Если 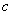 - неслучайная величина, то

.

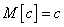Сформулированное свойство является достаточно очевидным; доказать его можно, рассматривая неслучайную величину 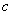 как частный вид случайной, при одном возможном значении с вероятностью единица; тогда по общей формуле для математического ожидания:

.

 

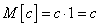2. Дисперсия неслучайной величины

 

Если 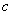 - неслучайная величина, то

.

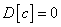Доказательство. По определению дисперсии

.

 

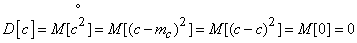3. Вынесение неслучайной величины за знак математического ожидания

 

Если 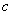 - неслучайная величина, а 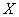- случайная, то

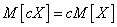,                 (10.2.1)

т. е. неслучайную величину можно выносить за знак математического ожидания.

Доказательство.

а) Для прерывных величин

.

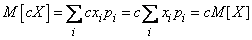б) Для непрерывных величин

.

 

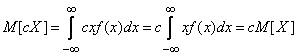4. Вынесение неслучайной величины за знак дисперсии и среднего квадратического отклонения

 

Если 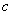 - неслучайная величина, а  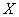- случайная, то

,                  (10.2.2)

т. е. неслучайную величину можно выносить за знак дисперсии, возводя ее в квадрат.

Доказательство. По определению дисперсии

.

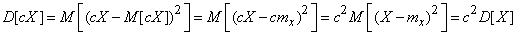Следствие

,

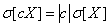т. е. неслучайную величину можно выносить за знак среднего квадратического отклонения ее абсолютным значением. Доказательство получим, извлекая корень квадратный из формулы (10.2.2) и учитывая, что с.к.о. - существенно положительная величина.

 

5. Математическое ожидание суммы случайных величин

 

Докажем, что для любых двух случайных величин 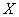 и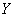 

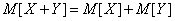,                          (10.2.3)

т. е. математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий.

Это свойство известно под названием теоремы сложения математических ожиданий.

Доказательство.

а) Пусть 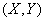 - система прерывных случайных величин. Применим к сумме случайных величин общую формулу (10.1.6) для математического ожидания функции двух аргументов:

.

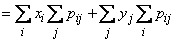Ho 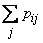 представляет собой не что иное, как полную вероятность того, что величина  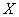примет значение :

;

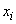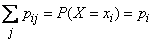следовательно,

.

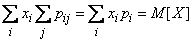Аналогично докажем, что

,

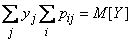и теорема доказана.

б) Пусть 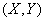 - система непрерывных случайных величин. По формуле (10.1.7)

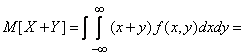
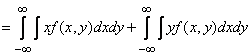.                  (10.2.4)

Преобразуем первый из интегралов (10.2.4):

;

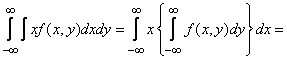
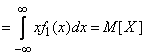аналогично

,

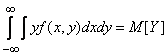и теорема доказана.

Следует специально отметить, что теорема сложения математических ожиданий справедлива для любых случайных величин - как зависимых, так и независимых.

Теорема сложения математических ожиданий обобщается на произвольное число слагаемых:

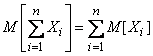,                    (10.2.5)

т. е. математическое ожидание суммы нескольких случайных величин равно сумме их математических ожиданий.

Для доказательства достаточно применить метод полной индукции.

 

6. Математическое ожидание линейной функции

 

Рассмотрим линейную функцию нескольких случайных аргументов :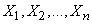

,

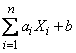где 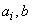 - неслучайные коэффициенты. Докажем, что

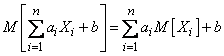,                         (10.2.6)

т. е. математическое ожидание линейной функции равно той же линейной функции от математических ожиданий аргументов.

Доказательство. Пользуясь теоремой сложения м. о. и правилом вынесения неслучайной величины за знак м. о., получим:

.

 

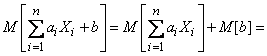
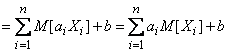7. Диспepсия суммы случайных величин

 

Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный корреляционный момент:

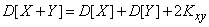.                 (10.2.7)

Доказательство. Обозначим

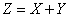.                             (10.2.8)

По теореме сложения математических ожиданий

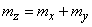.                       (10.2.9)

Перейдем от случайных величин 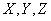 к соответствующим центрированным величинам 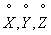. Об этом говорит сайт https://intellect.icu . Вычитая почленно из равенства (10.2.8) равенство (10.2.9), имеем:

.

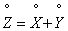По определению дисперсии

,

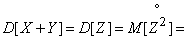
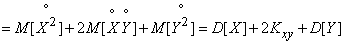что и требовалось доказать.

Формула (10.2.7) для дисперсии суммы может быть обобщена на любое число слагаемых:

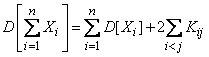,            (10.2.10)

где 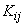 - корреляционный момент величин 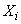,  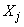знак 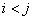 под суммой обозначает, что суммирование распространяется на все возможные попарные сочетания случайных величин .

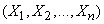Доказательство аналогично предыдущему и вытекает из формулы для квадрата многочлена.

Формула (10.2.10) может быть записана еще в другом виде:

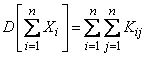,                                 (10.2.11)

где двойная сумма распространяется на все элементы корреляционной матрицы системы величин 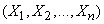, содержащей как корреляционные моменты, так и дисперсии.

Если все случайные величины 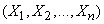, входящие в систему, некоррелированы (т. е.  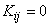при 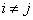), формула (10.2.10) принимает вид:

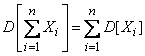,                                 (10.2.12)

т. е. дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых.

Это положение известно под названием теоремы сложения дисперсий.

 

8. Дисперсия линейной функции

 

Рассмотрим линейную функцию нескольких случайных величин.

,

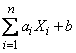где 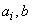 - неслучайные величины.

Докажем, что дисперсия этой линейной функции выражается формулой

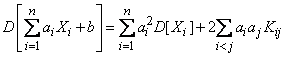,                     (10.2.13)

где 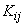 - корреляционный момент величин , .

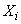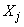Доказательство. Введем обозначение:

.

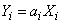Тогда

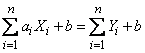.                      (10.2.14)

Применяя к правой части выражения (10.2.14) формулу (10.2.10) для дисперсии суммы и учитывая, что 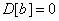, получим:

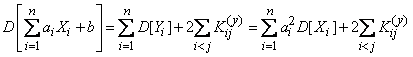,       (10.2.15)

где 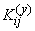 - корреляционный момент величин :

.

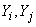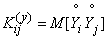Вычислим этот момент. Имеем:

;

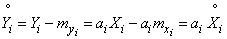аналогично

.

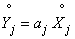Отсюда

.

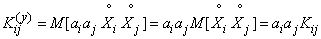Подставляя это выражение в (10.2.15), приходим к формуле (10.2.13).

В частном случае, когда все величины 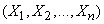 некоррелированны, формула (10.2.13) принимает вид:

,                     (10.2.16)

т. е. дисперсия линейной функции некоррелированных случайных величин равна сумме произведений квадратов коэффициентов на дисперсии соответствующих аргументов.

 

9. Математическое ожидание произведения случайных величин

 

Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:

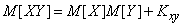.                        (10.2.17)

Доказательство. Будем исходить из определения корреляционного момента:

,

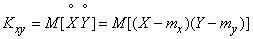где

; .

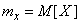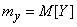Преобразуем это выражение, пользуясь свойствами математического ожидания:

,

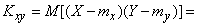
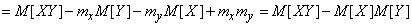что, очевидно, равносильно формуле (10.2.17).

Если случайные величины 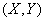 некоррелированны 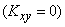, то формула (10.2.17) принимает вид:

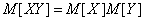,                                  (10.2.18)

т. е. математическое ожидание произведения двух некоррелированных случайных величин равно произведению их математических ожиданий.

Это положение известно под названием теоремы умножения математических ожиданий.

Формула (10.2.17) представляет собой не что иное, как выражение второго смешанного центрального момента системы через второй смешанный начальный момент и математические ожидания:

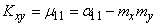.                              (10.2.19)

Это выражение часто применяется на практике при вычислении корреляционного момента аналогично тому, как для одной случайной величины дисперсия часто вычисляется через второй начальный момент и математическое ожидание.

Теорема умножения математических ожиданий обобщается и на произвольное число сомножителей, только в этом случае для ее применения недостаточно того, чтобы величины были некоррелированны, а требуется, чтобы обращались в нуль и некоторые высшие смешанные моменты, число которых зависит от числа членов в произведении. Эти условия заведомо выполнены при независимости случайных величин, входящих в произведение. В этом случае

,                   (10.2.20)

т. е. математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.

Это положение легко доказывается методом полной индукции.

 

10. Дисперсия произведения независимых случайных величин

 

Докажем, что для независимых величин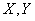 

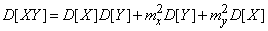.              (10.2.21)

Доказательство. Обозначим 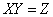. По определению дисперсии

.

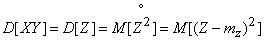Так как величины 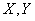 независимы,  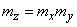и

.

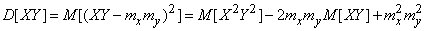При независимых 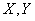 величины  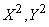тоже независимы; следовательно,

,  

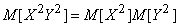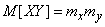
и

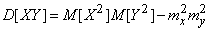.                 (10.2.22)

Но 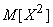 есть не что иное, как второй начальный момент величины 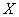, и, следовательно, выражается через дисперсию:

;

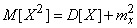аналогично

.

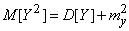Подставляя эти выражения в формулу (10.2.22) и приводя подобные члены, приходим к формуле (10.2.21).

В случае, когда перемножаются центрированные случайные величины (величины с математическими ожиданиями, равными нулю), формула (10.2.21) принимает вид:

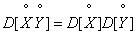,                        (10.2.23)

т. е. дисперсия произведения независимых центрированных случайных величин равна произведению их дисперсий.

 

11. Высшие моменты суммы случайных величин

 

В некоторых случаях приходится вычислять высшие моменты суммы независимых случайных величин. Докажем некоторые относящиеся сюда соотношения.

1) Если величины 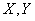 независимы, то

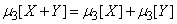.              (10.2.24)

Доказательство.

,

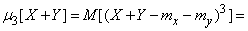
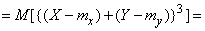
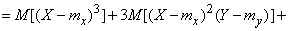
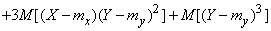откуда по теореме умножения математических ожиданий

.

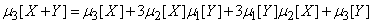Но первый центральный момент 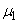 для любой величины равен нулю; два средних члена обращаются в нуль, и формула (10.2.24) доказана.

Соотношение (10.2.24) методом индукции легко обобщается на произвольное число независимых слагаемых:

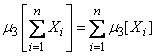.                   (10.2.25)

2) Четвертый центральный момент суммы двух независимых случайных величин выражается формулой

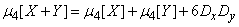.                      (10.2.26)

где 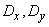 - дисперсии величин  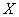и .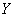

Доказательство совершенно аналогично предыдущему.

Методом полной индукции легко доказать обобщение формулы (10.2.26) на произвольное число независимых слагаемых:

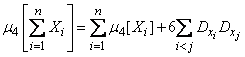.                    (10.2.27)

Аналогичные соотношения в случае необходимости легко вывести и для моментов более высоких порядков.

 

12. Сложение некоррелированных случайных векторов

 

Рассмотрим на плоскости 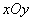 два некоррелированных случайных вектора: вектор  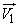с составляющими  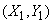и вектор  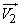с составляющими  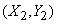(рис. 10.2.1).

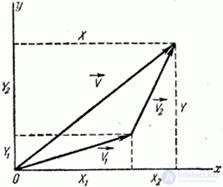
Рис. 10.2.1

Рассмотрим их векторную сумму:

,

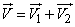т. е. вектор с составляющими:

,

.

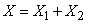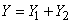Требуется определить числовые характеристики случайного вектора 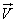 - математические ожидания 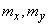, дисперсии и корреляционный момент составляющих: .

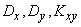По теореме сложения математических ожиданий:

;

.

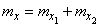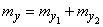По теореме сложения дисперсий

;

.

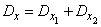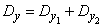Докажем, что корреляционные моменты также складываются:

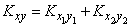,             (10.2.28)

где 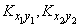 - корреляционные моменты составляющих каждого из векторов  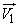и .

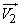Доказательство. По определению корреляционного момента:

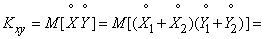
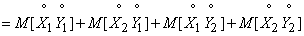.                 (10.2.29)

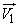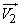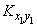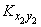Так как векторы  и  некоррелированны, то два средних члена в формуле (10.2.29) равны нулю; два оставшихся члена представляют собой  и ; формула (10.2.28) доказана.

Формулу (10.2.28) иногда называют «теоремой сложения корреляционных моментов».

Теорема легко обобщается на произвольное число слагаемых. Если имеется две некоррелированные системы случайных величин, т. е. два 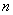-мерных случайных вектора:

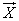 с составляющими ,

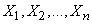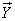 с составляющими ,

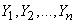то их векторная сумма

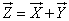
имеет корреляционную матрицу, элементы которой получаются суммированием элементов корреляционных матриц слагаемых:

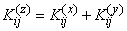,              (10.2.30)

где 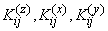 обозначают соответственно корреляционные моменты величин ;; .

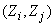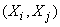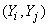Формула (10.2.30) справедлива как при 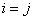, так и при 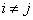. Действительно, составляющие вектора  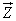равны:

По теореме сложения дисперсий

,

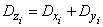или в других обозначениях

.

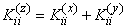По теореме сложения корреляционных моментов при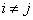 

.

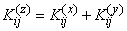В математике суммой двух матриц называется матрица, элементы которой получены сложением соответствующих элементов этих матриц. Пользуясь этой терминологией, можно сказать, что корреляционная матрица суммы двух некоррелированных случайных векторов равна сумме корреляционных матриц слагаемых:

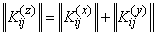 .                  (10.2.31)

Это правило по аналогии с предыдущими можно назвать «теоремой сложения корреляционных матриц».

 

Информация, изложенная в данной статье про теоремы о числовых характеристиках , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое теоремы о числовых характеристиках и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ