12.1. Закон распределения монотонной функции одного случайного аргумента кратко

Привет, Вы узнаете о том , что такое закон распределения монотонной функции одного случайного аргумента, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон распределения монотонной функции одного случайного аргумента , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В предыдущих главах мы познакомились с методами определения числовых характеристик функций случайных величин; главное удобство этих методов в том, что они не требуют нахождения законов распределения функций. Однако иногда возникает необходимость в определении не только числовых характеристик, но и законов распределения функций.

 

Начнем с рассмотрения наиболее простой задачи, относящейся к этому классу: задачи о законе распределения функции одного случайного аргумента. Так как для практики наибольшее значение имеют непрерывные случайные величины, будем решать задачу именно для них.

Имеется непрерывная случайная величина 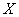 с плотностью распределения . Другая случайная величина 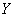 связана с нею функциональной зависимостью:

.

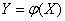Требуется найти плотность распределения величины .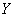

Рассмотрим участок оси абсцисс 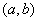, на котором лежат все возможные значения величины 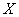, т. е.

.

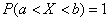В частном случае, когда область возможных значений 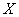 ничем не ограничена, , .

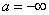Способ решения поставленной задачи зависит от поведения функции 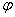 на участке 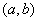: возрастает ли она на этом участке или убывает, или колеблется.

В данном 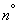 мы рассмотрим случай, когда функция  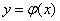участке  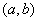монотонна. При этом отдельно проанализируем два случая: монотонного возрастания и монотонного убывания функции.

1. Функция 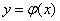 на участке  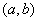монотонно возрастает (рис. 12.1.1). Когда величина  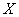принимает различные значения на участке 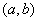, случайная точка  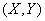перемещается только по кривой 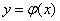; ордината этой случайной точки полностью определяется ее абсциссой.

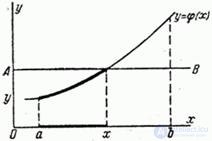
Рис. Об этом говорит сайт https://intellect.icu . 12.1.1.

Обозначим 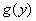 плотность распределения величины 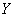. Для того чтобы определить 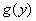, найдем сначала функцию распределения величины :

.

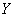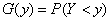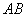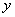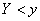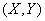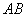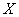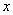Проведем прямую , параллельную оси абсцисс на расстоянии  от нее (рис. 12.1.1). Чтобы выполнялось условие , случайная точка  должна попасть на тот участок кривой, который лежит ниже прямой ; для этого необходимо и достаточно, чтобы случайная величина  попала на участок оси абсцисс от  до , где 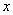 - абсцисса точки пересечения кривой  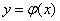и прямой 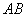. Следовательно,

.

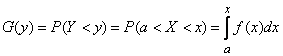Верхний предел интеграла 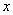 можно выразить через :

,

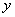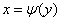где 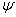 - функция, обратная функции 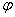. Тогда

.              (12.1.1)

Дифференцируя интеграл (12.1.1) по переменной 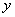, входящей в верхний предел, получим:

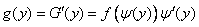.        (12.1.2)

 

2. Функция 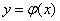 на участке  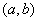монотонно убывает (рис. 12.1.2).

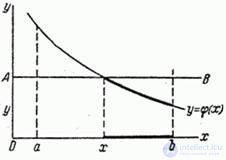
Рис. 12.1.2.

В этом случае

,

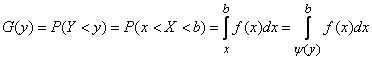откуда

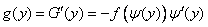.                  (12.1.3)

Сравнивая формулы (12.1.2) и (12.1.3), замечаем, что они могут быть объединены в одну:

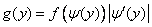.                    (12.1.4)

Действительно, когда 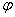 возрастает, ее производная (а значит, и 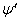) положительна. При убывающей функции  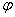производная  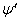отрицательна, но зато перед ней в формуле (12.1.3) стоит минус. Следовательно, формула (12.1.4), в которой производная берется по модулю, верна в обоих случаях. Таким образом, задача о законе распределения монотонной функции решена.

Пример. Случайная величина 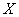 подчинена закону Коши с плотностью распределения:

.

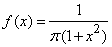Величина 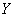 связана с  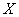зависимостью

.

Найти плотность распределения величины .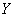

Решение. Так как функция 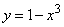 монотонна на участке 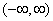, можно применить формулу (12.1.4). Решение задачи оформим в виде двух столбцов: в левом будут помещены обозначения функций, принятые в общем решении задачи, в правом - конкретные функции, соответствующие данному примеру:

 

 

Информация, изложенная в данной статье про закон распределения монотонной функции одного случайного аргумента , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое закон распределения монотонной функции одного случайного аргумента и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про закон распределения монотонной функции одного случайного аргумента