13.4. Обобщенная теорема Чебышева. Теорема Маркова кратко

Привет, Вы узнаете о том , что такое теорема чебышева, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теорема чебышева, теорема маркова , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

теорема чебышева легко может быть обобщена на более сложный случай, а именно когда закон распределения случайной величины  от опыта к опыту не остается одним и тем же, а изменяется. Тогда вместо среднего арифметического наблюденных значений одной и той же величины  с постоянными математическим ожиданием и дисперсией мы имеем дело со средним арифметическим  различных случайных величин, с различными математическими ожиданиями и дисперсиям. Оказывается, что и в этом случае при соблюдения некоторых условий среднее арифметическое является устойчивым и сходится по вероятности к определенной неслучайной величине.

 

Обобщенная теорема Чебышева формулируется следующим образом. Если

 -

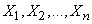независимые случайные величины с математическими ожиданиями

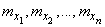
и дисперсиями

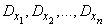
и если все дисперсии ограничены сверху одним и тем же числом :

                                                               ,                              

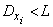
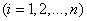то при возрастании  среднее арифметическое наблюденных значений величин 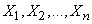 сходится по вероятности к среднему арифметическому их математических ожиданий.

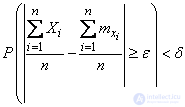
Запишем эту теорему в виде формулы. Об этом говорит сайт https://intellect.icu . Пусть 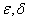 - сколь угодно малые положительные числа. Тогда при достаточно большом 

.                  (13.4.1)

Доказательство. Рассмотрим величину

.

Ее математическое ожидание равно:

,

а дисперсия

.

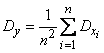Применим к величине 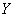 неравенство Чебышева:

,

или

.              (13.4.2)

Заменим в правой части неравенства (13.4.2) каждую из величин 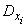 большей величиной . Тогда неравенство только усилится:

.

Как бы мало ни было , можно выбрать  настолько большим, чтобы выполнялось неравенство

;

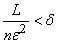тогда

,

откуда, переходя к противоположному событию, получим доказываемое неравенство (13.4.1).

Закон больших чисел может быть распространен и на зависимые случайные величины. Обобщение закона больших чисел на случай зависимых случайных величин принадлежит А. А. Маркову.

теорема маркова . Если имеются зависимые случайные величины 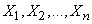 и если при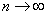 

,

то среднее арифметическое наблюденных значений случайных величин 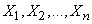 сходится по вероятности к среднему арифметическому их математических ожиданий. Доказательство. Рассмотрим величину

.

Очевидно,

.

Применим к величине 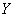 неравенство Чебышева:

.

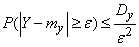Так как по условию теоремы при 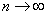 , то при достаточно большом 

,

или, переходя к противоположному событию,

,

что и требовалось доказать.

Информация, изложенная в данной статье про теорема чебышева , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое теорема чебышева, теорема маркова и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про теорема чебышева