Вариограмма

Привет, Вы узнаете о том , что такое вариограмма, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое вариограмма , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В пространственной статистике теоретическая вариограмма - функция, описывающая степень пространственной зависимости пространственного случайного поля или случайного процесса .

В случае конкретного примера из области добычи золота вариограмма даст меру того, насколько две пробы, взятые из области добычи, будут различаться в процентном содержании золота в зависимости от расстояния между этими пробами. Образцы, взятые далеко друг от друга, будут отличаться больше, чем образцы, взятые близко друг к другу.

Вариограмма — статистический момент второго порядка, использующийся в геостатистике для анализа и моделирования пространственной корреляции.

Вариограмма для значений пространственной переменной в двух точках и , разделенных вектором , определяется вариацией (дисперсией) разницы значений переменной в этих точках . При этом величина называется полувариограммой:

Если принять “внутреннюю (intrinsic) гипотезу”, о том что приращение функции является слабо стационарным, то дисперсия и среднее приращения существуют и не зависят от расположения точки

Определение

Вариограмма

вариограмма был впервые определен Матероном (Matheron, 1963) как половина средней квадратичной разницы между точками ( а также ) разделены на расстоянии . Формально

где это точка в геометрическом поле , а также это значение в этой точке. Например, предположим, что нас интересует содержание железа в образцах почвы в каком-то регионе или поле.. будет содержание (например, в мг железа на кг почвы) железа в некотором месте , где имеет координаты широты, долготы и высоты. Тройной интеграл имеет более трех измерений.представляет собой интересующее расстояние разноса (например, в м или км). Чтобы получить вариограмму для заданного, будут выбраны все пары точек на этом точном расстоянии. На практике невозможно произвести выборку везде, поэтому вместо нее используется эмпирическая вариограмма .

Вариограмма определяется как

  γ(si,sj) = ½ var(Z(si) - Z(sj)),

где var является дисперсией.

Если два местоположения, si и sj, близки друг к другу в единицах измерения расстояния d(si, sj), можно ожидать, что они похожи, так что разность их значений, Z(si) – Z(sj), будет мала. По мере дальнейшего удаления i и sj друг от друга они становятся менее похожи, поэтому разность их значений, Z(si) – Z(sj), станет больше. Это можно видеть на следующем рисунке, на котором показано, из чего состоит типичная вариограмма.

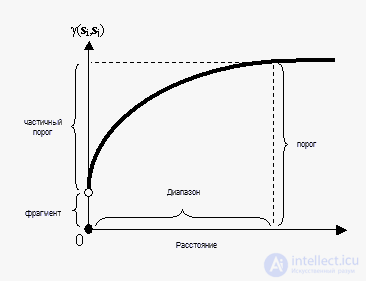
Обратите внимание, что дисперсия разности увеличивается с расстоянием, поэтому вариограмму можно рассматривать как функцию несходства. Имеются несколько терминов, которые часто ассоциируются с этой функцией, и они также используются в ArcGIS Geostatistical Analyst Extension. Высота, которую вариограмма достигает при ее выравнивании, называется порогом. Она часто состоит из двух частей: разрыв в начале координат, называемый эффектом самородка, и частичный порог; вместе они составляют порог. Эффект самородка может быть далее разделен на погрешность измерений и вариацию на микроуровне. Эффект самородка является просто суммой погрешности измерений и вариации на микроуровне, и поскольку какой-нибудь из этих компонентов может быть равен нулю, эффект самородка может целиком состоять из первого или второго компонента. Высота, на которой вариограмма выравнивается до порога, называется диапазоном

Вариограмма

Вариограмма определяется как дисперсия разницы между значениями полей в двух точках ( а также , обратите внимание на изменение обозначений с к а также к ) между реализациями поля (Cressie 1993):

или, другими словами, это в два раза больше вариограммы. Если пространственное случайное поле имеет постоянное среднее значение, это эквивалентно ожидаемому квадрату приращения значений между местоположениями а также (Wackernagel 2003) (где а также точки в пространстве и, возможно, во времени):

В случае стационарного процесса вариограмму и вариограмму можно представить как функцию разницы только между местоположениями, следующим соотношением (Cressie 1993):

Если процесс, кроме того, изотропный , то вариограмма и вариограмма могут быть представлены функцией расстояния только (Cressie 1993):

Индексы или обычно не пишутся. Об этом говорит сайт https://intellect.icu . Эти термины используются для всех трех форм функции. Более того, термин «вариограмма» иногда используется для обозначения вариограммы, а символ иногда используется для вариограммы, что вносит некоторую путаницу.

Свойства

Согласно (Cressie 1993, Chiles and Delfiner 1999, Wackernagel 2003) теоретическая вариограмма имеет следующие свойства:

• Вариограмма неотрицательная , так как это ожидание квадрата.
• Вариограмма на расстоянии 0 всегда 0, так как .
• Функция является вариограммой тогда и только тогда, когда она является условно отрицательно определенной функцией, т.е. для всех весов при условии и локации он содержит:

  

  что соответствует тому, что дисперсия из дается отрицанием этой двойной суммы и должен быть неотрицательным.
• Как следствие, вариограмма может быть прерывистой только в начале координат. Высота скачка в исходной точке иногда называется эффектом самородка или самородка.
• Если ковариационная функция стационарного процесса существует, она связана с вариограммой соотношением

  

  Для нестационарного процесса необходимо добавить квадрат разницы между ожидаемыми значениями в обеих точках:

  

• Если стационарное случайное поле не имеет пространственной зависимости (т.е. если ) вариограмма - это постоянная везде, кроме начала координат, где он равен нулю.
• является симметричной функцией.
• Как следствие, - четная функция .
• Если случайное поле стационарно и эргодично ,соответствует дисперсии поля. Граница вариограммы также называется ее порогом .

Эмпирическая вариограмма и применение

Как правило, необходима эмпирическая вариограмма, поскольку информация о выборке доступен не для всех мест. Информация об образце, например, может быть концентрацией железа в образцах почвы или интенсивностью пикселей на камере. Каждый фрагмент информации об образце имеет координаты для 2D образца пространства, где а также являются географическими координатами. В случае железа в почве пространство для образца может быть трехмерным. Если также есть временная изменчивость (например, содержание фосфора в озере), то может быть четырехмерным вектором . Для случая, когда размеры имеют разные единицы (например, расстояние и время), тогда коэффициент масштабированияможет применяться к каждому, чтобы получить модифицированное евклидово расстояние.

Выборочные наблюдения обозначены . Образцы можно взять ввсего разные локации. Это предоставит как набор образцов в местах . Обычно графики показывают значения вариограммы как функцию разделения точек выборки.. В случае эмпирической вариограммы интервалы разделительных расстояний используются, а не точные расстояния, и обычно предполагаются изотропные условия (т. е. что это только функция и не зависит от других переменных, таких как центральное положение). Тогда эмпирическая вариограмма можно рассчитать для каждого бункера:

Или, другими словами, каждая пара точек, разделенных (плюс или минус некоторый диапазон допуска ширины бункера ) найдены. Они образуют набор точек. Количество этих точек в этой корзине равно. Тогда для каждой пары точек, квадрат разницы в наблюдении (например, содержание образца почвы или интенсивность пикселей) находится (). Эти квадраты разностей складываются и нормализуются натуральным числом.. По определению результат делится на 2 для вариограммы на этом разделении.

Для скорости вычислений нужны только уникальные пары точек. Например, для 2 пар наблюдений [] взяты из локаций с разделением только [] необходимо рассматривать, поскольку пары [] не предоставляют никакой дополнительной информации.

Эмпирическая вариограмма используется в геостатистике в качестве первой оценки (теоретической) вариограммы необходимой для пространственной интерполяции кригинге .

Согласно (Cressie 1993), для наблюдений из стационарного случайного поля , эмпирическая вариограмма с допуском запаздывания 0 является несмещенной оценкой теоретической вариограммы из-за:

Параметры вариограммы

Для описания вариограмм часто используются следующие параметры:

• самородок : Высота скачка вариограммы на разрыве в начале координат.
• подоконник : Предел вариограммы, стремящийся к бесконечному расстоянию запаздывания.
• спектр : Расстояние, на котором разница между вариограммой и порогом становится незначительной. В моделях с фиксированным порогом это расстояние, на котором он достигается в первую очередь; для моделей с асимптотическим порогом обычно принимается расстояние, когда полувариантность впервые достигает 95% порога.

Модели вариограмм

Эмпирическая вариограмма не может быть рассчитана на каждом расстоянии запаздывания. и из-за различий в оценке не гарантируется, что это действительная вариограмма, как определено выше. Однако для некоторых геостатистических методов, таких как кригинг, требуются действительные вариограммы. Таким образом, в прикладной геостатистике эмпирические вариограммы часто аппроксимируются функцией модели, обеспечивающей достоверность (Chiles & Delfiner 1999). Вот некоторые важные модели (Chiles & Delfiner 1999, Cressie 1993):

• Модель экспоненциальной вариограммы

• Модель сферической вариограммы

• Модель гауссовой вариограммы

Параметр имеет разные значения в разных справочниках из-за неоднозначности определения диапазона. Например- значение, используемое в (Chiles & Delfiner 1999). В функция равна 1, если и 0 в противном случае.

Обсуждение

В геостатистике используются три функции для описания пространственной или временной корреляции наблюдений: это коррелограмма , ковариация и вариограмма . Последний также проще называют вариограммой . Вариограмма выборки , в отличии от вариограммы и вариограммы, показывает , где значительная степень пространственной зависимости в выборочном пространстве или выборках единиц рассеиваются в случайность , когда дисперсия точка зрения во время или на место упорядоченного множество приведена в зависимости от дисперсии множества и нижние пределы его доверительных интервалов 99% и 95%.

Вариограмма является ключевой функцией геостатистики, поскольку она будет использоваться для соответствия модели временной / пространственной корреляции наблюдаемого явления. Таким образом, проводится различие между экспериментальной вариограммой, которая представляет собой визуализацию возможной пространственной / временной корреляции, и моделью вариограммы, которая в дальнейшем используется для определения весов функции кригинга . Обратите внимание , что экспериментальный вариограмма является эмпирической оценкой ковариации в виде процесса гауссовой . Таким образом, он не может быть положительно определенным и, следовательно, не может напрямую использоваться в кригинге., без ограничений и дальнейшей обработки. Это объясняет, почему используется только ограниченное количество моделей вариограмм: чаще всего это линейная, сферическая, гауссова и экспоненциальная модели.

Отношение между вариограммой и функцией ковариации

Между вариограммой и функцией ковариации имеется связь.

 γ(si, sj) = sill - C(si, sj),

Эту связь можно видеть на рисунках. Из-за этой эквивалентности можно сделать интерполяцию в ArcGIS Geostatistical Analyst Extension с использованием какой-либо из этих функций. (Все вариограммы в ArcGIS Geostatistical Analyst Extension имеют пороги).

Вариограммы и ковариации не могут быть только функцией. Чтобы интерполяции имели неотрицательные стандартные ошибки кригинга, в качестве вариограмм и ковариаций могут использоваться только некоторые функции. ArcGIS Geostatistical Analyst Extension предлагает несколько приемлемых вариантов, и для данных можно попробовать использовать разные варианты. Можно также иметь модели, составленные добавлением нескольких моделей – такое построение предоставляет допустимые модели, и в ArcGIS Geostatistical Analyst Extension можно добавить до четырех из них. Имеется несколько случаев, когда существуют вариограммы, но функции ковариации – нет. Например, имеется линейная вариограмма, но у нее нет порога, и нет соответствующей функции ковариации. В ArcGIS Geostatistical Analyst Extension используются модели только с порогами. Отсутствуют надежные правила выбора "наилучшей" модели вариограммы. Рассматривая эмпирическую вариограмму или функцию ковариации, можно выбрать наиболее подходящую модель. Можно также в качестве руководства использовать проверку и перекрестную проверку.

Функция ковариации определяется как

C(si, sj) = cov(Z(si), Z(sj)),

где cov является ковариацией.

Ковариация является масштабируемой версией корреляции. Если два местоположения, si и sj, близки друг к другу, можно ожидать, что они похожи, и их ковариация (корреляция) будет большой. По мере дальнейшего удаления si и sj друг от друга они становятся менее похожи, и их ковариация стремится к нулю. Это можно видеть на следующем рисунке, на котором показано, из чего состоит типичная функция ковариации.

Обратите внимание, что функция ковариации уменьшается с расстоянием, поэтому ее можно рассматривать как функцию сходства.

Понятия, связанные с данным

Квадрат в вариограмме, например , могут быть заменены разными степенями: Мадограмма определяется с абсолютной разницей ,, а родограмма определяется квадратным корнем из абсолютной разности,. Оценщики, основанные на этих более низких степенях, считаются более устойчивыми к выбросам . Их можно обобщить как «вариограмму порядка α »,

,

в котором вариограмма 2-го порядка, мадограмма - вариограмма 1-го порядка, а родограмма - вариограмма 0,5-го порядка.

Когда вариограмма используется для описания корреляции различных переменных, она называется кросс-вариограммой . В ко-кригинге используются кросс-вариограммы . Если переменная является двоичной или представляет собой классы значений, тогда речь идет о индикаторных вариограммах . Индикаторная вариограмма используется в индикаторном кригинге .

Примеры исследований

• Эмпирические вариограммы для пространственно-временной изменчивости усредненного по столбцу углекислого газа использовались для определения критериев совпадения для спутниковых и наземных измерений.
• Эмпирические вариограммы рассчитывались для плотности неоднородного материала (гильсокарбон).
• Эмпирические вариограммы рассчитываются на основе наблюдений за сильными колебаниями грунта в результате землетрясений . Эти модели используются для оценки сейсмического риска и потерь пространственно распределенной инфраструктуры.

См. Также

• Ковариационная функция
• Полувариантность

Исследование, описанное в статье про вариограмма, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое вариограмма и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ