Закон полного математического ожидания( правило башни , закон Адама ,теорема сглаживания ) кратко

В теории вероятностей утверждение известно как закон полного математического ожидания , закон повторных чаяний , правило башни , закон адама или теорема сглаживания утверждает, что если — случайная величина , с определенным ожиданием , а - произвольная случайная величина на том вероятностном пространстве .

то есть значение надежды условного матожидания значение для определенного равно матождеству .

В специальном случае, для - конечного или счетного разбиения пространства элементарных событий , тогда

Предположим, что две фабрики поставляют на рынок лампочки . Лампочки с завода работают в среднем 5000 часов, в то время как лампы завода работают в среднем на протяжении 4000 часов. Известно, что фабрика снабжает 60% от общего количества имеющихся ламп. Какова ожидаемая продолжительность работы приобретенной лампочки?

Применяя закон полного матожидания получим:

где

• - продолжительность работы лампочки;
• — вероятность того, что купленная лампочка изготовлена ​​на заводе X;
• – вероятность, что купленная лампочка изготовлена ​​на заводе Y;
• - ожидаемая продолжительность работы лампочки изготовленной на заводе X;
• – ожидаемая продолжительность работы лампочки изготовленной на заводе Y.

Следовательно, ожидаемая продолжительность работы каждой приобретенной лампочки равна 4600 часам.

Доказательство для конечных и счисленных случаев

Пусть случайные величины да определены на одном вероятностном пространстве, допустим конечное или счисленное множество конечных значений. Предположим что определена, то ест . Если - измельчение вероятностного пространства Ω , то

Доказательство

Если ряд окончен, то можем изменить порядок суммирования и предыдущее выражение запишется

Если же, с другой стороны, ряд бесконечен, то его сходимость не может быть условной из-за предположения, что Ряд сходим абсолютно если оба, - конечной и расхожей до бесконечности, если ли или – бесконечное. В обоих случаях порядок суммирования можно изменить без изменения суммы.

Доказательство в общем случае

Пусть — вероятностное пространство с определенными на нем σ-алгебрами . Для случайной величины на таком пространстве, закон сглаживания утверждает, что если - определенное, то есть , тогда

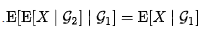. (почти наверняка)

Доказательство . Благодаря тому, что условное матпредложение это производная Радона – Никодима , доведение закона сглаживания сводится к проверке следующих двух свойств:

• есть - измеримой
• для всех

Первое из этих свойств вытекает из определения условного матожидания. Для доказывания второго,

следовательно интеграл определен (не равен±∞).

Второе свойство правильно, ибо следует

Вывод. В особом случае, когда и ), закон сглаживания сводится к

Доказательство формулы разбиения

где - характеристическая функция множественного числа .

Если разбиение - конечное, то, по свойству линейности, предварительное выражение записывается в виде

что и нужно было показать.

Если же разбиение - бесконечное, то применяя теорему о мажированной сходимости можем показать

Действительно, для каждого ,

Поскольку каждый элемент множестваΩ принадлежит определенному элементу измельчения , легко проверить что последовательность поточно сходящаяся к X. По предположению в утверждении, . Применяя теорему о мажированной сходимости получаем желаемое утверждение.

Вау!! 😲 Ты еще не читал? Это зря!

• Основная теорема покера для одного практического применения.
• Формула полной вероятности
• Закон полной дисперсии
• Закон полной ковариации
• Закон совокупной кумуляции
• Распределение произведения двух случайных величин