12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону кратко

Привет, Вы узнаете о том , что такое закон распределения линейной функции от аргумента подчиненного нормальному закону, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое закон распределения линейной функции от аргумента подчиненного нормальному закону , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Пусть случайная величина 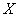 подчинена нормальному закону с плотностью:

,                (12.2.1)

а случайная величина 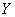 связана с нею линейной функциональной зависимостью:

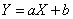.                (12.2.2)

где 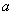 и 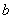 - неслучайные коэффициенты.

 

Требуется найти закон распределения величины .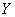

Оформим решение в виде двух столбцов, аналогично примеру предыдущего :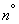

 

Преобразуя выражение 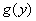, имеем:

,

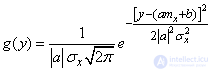а это есть не что иное, как нормальный закон с параметрами:

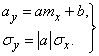                      (12.2.3)

Если перейти от средних квадратических отклонений к пропорциональным им вероятным отклонениям, получим:

.                            (12.2.4)

Таким образом мы убедились, что линейная функция от аргумента, подчиненного нормальному закону, также подчинена нормальному закону. Об этом говорит сайт https://intellect.icu . Чтобы найти центр рассеивания этого закона, нужно в выражение линейной функции вместо аргумента подставить его центр рассеивания. Чтобы найти среднее квадратическое отклонение этого закона, нужно среднее квадратическое отклонение аргумента умножить на модуль коэффициента при аргументе в выражении линейной функции. То же правило справедливо и для вероятных отклонений.

 

Информация, изложенная в данной статье про закон распределения линейной функции от аргумента подчиненного нормальному закону , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое закон распределения линейной функции от аргумента подчиненного нормальному закону и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про закон распределения линейной функции от аргумента подчиненного нормальному закону