Непрерывные случайные величины (НСВ) характеристики и примеры кратко

Привет, сегодня поговорим про непрерывные случайные величины, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое непрерывные случайные величины, нсв, непрерывная случайные величина , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Числовые характеристики непрерывных случайных величин нсв

Интегральная функция (функция распределения)

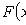
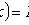
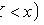
Свойства:

1) ;

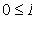
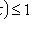2) ;

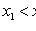
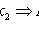
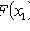
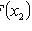3) ;

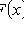
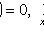
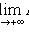
4) .

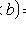
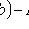
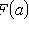Дифференциальная функция распределения (плотность вероятности)

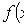
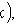
где F(x) - интегральная функция.

Свойства:

1) ;

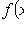
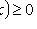2) ;

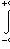
3) ;

4) .

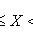
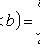
Числовые характеристики непрерывной случайной величины

Математическое ожидание

Дисперсия

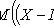
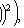
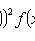
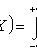
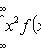
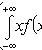
Некоторые законы распределения непрерывных случайных величин

Равномерное распределение

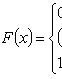
Нормальное распределение (распределение Гаусса)

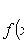
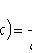
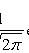
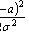
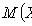
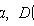
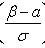
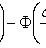
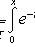
где - функция Лапласа;

Примеры абсолютно непрерывных распределений

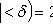
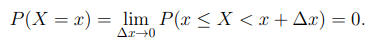
1) Равномерное распределение в отрезке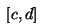

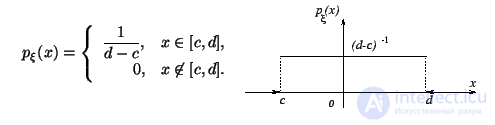
2) Показательное распределение с параметром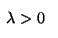

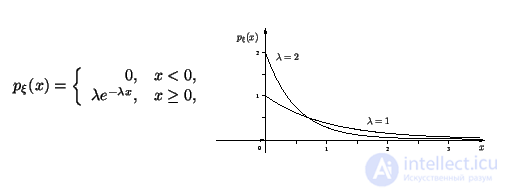
Показательное распределение называют также экспоненциальным.

3) Нормальное (или гауссовское) распределение

Пример

Задача Случайная величина X задана функцией распределения

1) Построить график функции F(x);

2) найти вероятности того, что в результате опыта случайная величина X примет значения, принадлежащие:

а) интервалу (1, 2; 1, 6);

б) отрезку [1, 7; 2, 3];

в) лучу {x : x > 1, 5};

г) лучу {x : x ≤ 1, 3}.

Решение.

1) Построим требуемый график (рис. 1).

Рис. 1
2) С помощью формулы (1) вычислим требуемые вероятности:

а) P(1,2 < X < 1,6) = F(1,6) − F(1,2).

Так как 1,2 ∈ (1; 2), то F(1,2) = (1, 2 − 1)2 , то есть F(1, 2) = 0, 04.
Аналогично, F(1, 6) = (1,6 − 1)2 ⇒ F(1, 6) = 0, 36.
Поэтому P(1,2 < X < 1,6) = 0,36 − 0,04 ⇒ P(1, 2 < X < 1, 6) = 0, 32.

б) Согласно формуле P(1,7 ≤ X ≤ 2,3) = F(2, 3) − F(1,7).
Так как 1,7 ∈ (1; 2), то F(1,7) = (1,7 − 1)² , то есть F(1,7) = 0,49.
В силу того, что 2,3 > 2, F(2,3) = 1.

Поэтому P(1,7 ≤ X ≤ 2,3) = 1 − 0,49 ⇒ P(1, 7 ≤ X ≤ 2, 3) = 0,51.

в) Представим луч {x : x > 1, 5} в виде бесконечного интервала (1,5; ∞).

Тогда, согласно формуле P(1, 5 < X < ∞) = F(∞) − F(1,5).
Так как 1,5 ∈ (1; 2), то F(1,5) = (1,5 − 1)² , то есть F(1,5) = 0, 25.
Так как F(∞) = 1,
то P(1,5 < X < ∞) = 1 − 0,25 ⇒ P(X > 1,5) = 0,75.

г) Как и в предыдущем задании, представим луч {x : x ≤ 1, 3} в виде
бесконечного множества (−∞; 1, 3].
Тогда, согласно той же формуле P(−∞ < X ≤ 1, 3) = F(1, 3)−F(−∞).
Так как 1, 3 ∈ (1; 2), то F(1, 3) = (1, 3 − 1)² , то есть F(1, 3) = 0,09.
Известно, что F(−∞) = 0.
Поэтому P(−∞ < X ≤ 1, 3) = 0, 09 − 0 ⇒ P(X ≤ 1, 3) = 0,09.

Объединяя результаты а)-г), получаем
P(1,2 < X < 1,6) = 0,32; P(1,7 ≤ X ≤ 2,3) = 0, 51;
P(X > 1,5) = 0,75; P(X ≤ 1,3) = 0,09.

Вау!! 😲 Ты еще не читал? Это зря!

• Случайные величины случайные величины , случайная величина ,
• Случайные события
• Смешанная случайная величина
• Многомерные случайные величины

На этом все! Теперь вы знаете все про непрерывные случайные величины, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое непрерывные случайные величины, нсв, непрерывная случайные величина и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про непрерывные случайные величины