Лекция
Привет, Вы узнаете о том , что такое композиция нормальных законов на плоскости, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое композиция нормальных законов на плоскости , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Пусть в системе координат 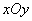 заданы два независимых случайных вектора:
заданы два независимых случайных вектора:  с составляющими
с составляющими 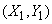 и
и 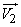 с составляющим
с составляющим 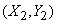 . Допустим, что каждый из них распределен нормально, причем параметры первого вектора равны
. Допустим, что каждый из них распределен нормально, причем параметры первого вектора равны
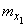 ,
,  ,
, 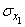 ,
,  ,
, 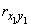 ,
,
а параметры второго -
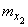 ,
, 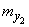 ,
, 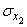 ,
, 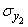 ,
, 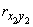 .
.
Требуется определить закон распределения случайного вектора 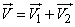 (рис. 12.8.1), составляющие которого равны:
(рис. 12.8.1), составляющие которого равны:
 ;
;
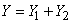 .
.

Рис. 12.8.1.
Не представляет трудности качественно доказать (аналогично тому как мы это сделали для случая композиции двух нормальных законов в  12.6), что вектор
12.6), что вектор 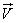 также распределен нормально. Мы примем это положение без специального доказательства.
также распределен нормально. Мы примем это положение без специального доказательства.
Определим параметры закона распределения вектора 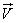 .
.
По теореме сложения математических ожиданий
 (12.8.1)
(12.8.1)
По теореме сложения дисперсий
 (12.8.2)
(12.8.2)
По теореме сложения корреляционных моментов
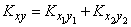 ,
,
или, переходя к коэффициентам корреляции,
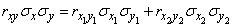 ,
,
откуда
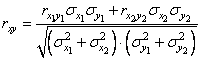 . (12.8.3)
. (12.8.3)
Таким образом, задача композиции нормальных законов на плоскости решается формулами (12.8.1), (12.8.2) и (12.8.3).
Эти формулы выведены для того случая, когда оба исходных нормальных закона (для векторов  и
и 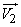 ) заданы в одной и той же координатной системе
) заданы в одной и той же координатной системе 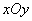 . На практике иногда встречается случай, когда нужно произвести композицию двух нормальных законов на плоскости, каждый из которых задан в своей системе координат, а именно в своих главных осях рассеивания. Дадим способ композиции нормальных законов для этого случая.
. На практике иногда встречается случай, когда нужно произвести композицию двух нормальных законов на плоскости, каждый из которых задан в своей системе координат, а именно в своих главных осях рассеивания. Дадим способ композиции нормальных законов для этого случая.
Пусть на плоскости 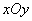 (рис. 12.8.2) даны два нормально распределенных некоррелированных случайных вектора
(рис. 12.8.2) даны два нормально распределенных некоррелированных случайных вектора  и
и 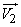 .
.

Рис. 12.8.2.
Каждый из векторов характеризуется своим единичным эллипсом рассеивания: вектор  - эллипсом с центром в точке
- эллипсом с центром в точке 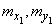 с полуосями
с полуосями 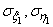 , из которых первая образует с осью
, из которых первая образует с осью 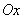 угол
угол  ; аналогичные характеристики для вектора
; аналогичные характеристики для вектора 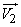 будут:
будут:  ,
,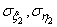 ,
,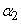 . Об этом говорит сайт https://intellect.icu . Требуется найти параметры единичного эллипса рассеивания, характеризующего вектор
. Об этом говорит сайт https://intellect.icu . Требуется найти параметры единичного эллипса рассеивания, характеризующего вектор 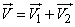 . Обозначим их
. Обозначим их
 ,
,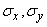 ,
,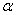 .
.
Так как положение центра рассеивания не зависит от выбора системы координат, очевидно, по-прежнему будут справедливы соотношения:
 ,
,
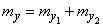 .
.
Для того чтобы найти элементы корреляционной матрицы вектора 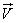 , спроектируем случайные точки, соответствующие векторам
, спроектируем случайные точки, соответствующие векторам  и
и 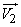 , на оси
, на оси 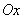 и
и 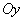 . Пользуясь формулой (10.3.3), получим:
. Пользуясь формулой (10.3.3), получим:
 (12.8.4)
(12.8.4)
Коэффициенты корреляции составляющих векторов  и
и 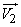 в системе координат
в системе координат 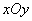 найдем из соотношения (9.2.2):
найдем из соотношения (9.2.2):
 (12.8.5)
(12.8.5)
Далее задача композиции нормальных законов на плоскости сводится к предыдущей. Зная 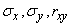 , можно найти углы, составленные осями суммарного эллипса с осью абсцисс, по формуле (9.2.2):
, можно найти углы, составленные осями суммарного эллипса с осью абсцисс, по формуле (9.2.2):
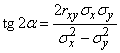 , (12.8.6)
, (12.8.6)
и главные средние квадратические отклонения - по формулам (9.2.4):
 (12.8.7)
(12.8.7)
Последние соотношении справедливы не только для средних квадратических отклонений, но и для пропорциональных им вероятных отклонений:
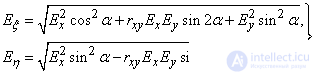 (12.8.8)
(12.8.8)
Перейдем к композиции произвольного числа нормальных законов на плоскости.
С наиболее простым случаем композиции произвольного числа формальных законов мы встречаемся тогда, когда главные оси рассеивания для всех законов, подлежащих композиции, параллельны друг другу. Тогда, выбирая координатные оси параллельно этим главным осям рассеивания, мы будем иметь дело с системами независимых случайных величин, и композиция нормальных законов выполняется по простым формулам:
 (12.8.9)
(12.8.9)
где  - главные средние квадратические отклонения соответствующих законов.
- главные средние квадратические отклонения соответствующих законов.
В случае, когда направления главных осей не совпадают, можно составить композицию нескольких нормальных законов тем же методом, которым мы пользовались выше для двух законов, т. е. проектируя складываемые случайные векторы на оси одной и той же системы координат.
На практике часто встречаются случаи, когда в числе законов, подлежащих композиции, встречаются так называемые «вырожденные» законы, т. е. законы, характеризующиеся эллипсом рассеивания, имеющим только одну полуось (другая равна нулю). Такие «вырожденные» законы дают рассеивание только в одном направлении. При композиции таких законов нужно поступать так же, как при композиции обычных законов, полагая некоторые параметры (средние квадратические или вероятные отклонения) равными нулю.
Пример 1. Ошибка бомбометания вызвана совместным действием следующих факторов:
1) техническое рассеивание бомб;
2) неточность прицеливания по дальности;
3) неточная наводка в боковом направлении.
Все эти факторы независимы. Техническое рассеивание бомб дает единичный эллипс рассеивания в виде круга радиусом 20 м. Ошибка прицеливания по дальности действует только в направлении полета и имеет среднее квадратическое отклонение 40 м; центр рассеивания сдвинут вперед по полету на 5 м. Ошибка боковой наводки действует только в направлении, перпендикулярном к полету, и имеет среднее квадратическое отклонение 30 м; центр рассеивания смещен вправо на 10 м. Найти параметры нормального закона, которому подчинена суммарная ошибка бомбометания, вызванная совместным действием всех перечисленных факторов.
Решение. Так как главные оси всех перечисленных в задаче эллипсов (из которых второй и третий вырождены) параллельны, то можно применить правило композиции нормальных законов с независимыми составляющими (формулы (12.8.9)). Выбирая ось 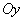 по направлению полета, ось
по направлению полета, ось 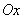 - перпендикулярно к нему, имеем:
- перпендикулярно к нему, имеем:
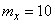 ,
, 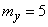 ,
,
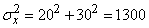 ,
, 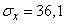 (м),
(м),
 ,
, 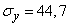 (м).
(м).
Пример 2. Производится воздушная стрельба с самолета по самолету; рассеивание точек попадания рассматривается на вертикальной плоскости, перпендикулярной к направлению стрельбы. Причины рассеивания точек попадания состоят в следующем:
1) ошибки, связанные с неоднородностью баллистики снарядов и колебаниями установки;
2) ошибки наводки;
3) ошибки, вызванные неточностью определения дальности;
4) инструментальные ошибки прицела.
Главные оси рассеивания, вызванного первой причиной, расположены горизонтально и вертикально, и главные средние квадратические отклонена равны соответственно 1 и 2 м; ошибка наводки дает круговое рассеивание со средним квадратическим отклонением 3 м; ошибка, вызванная неточностью определения дальности, дает рассеивание только вдоль оси, наклоненной к горизонту под углом 30°, со с.к.о. 4 м; инструментальные ошибки прицела дают круговое рассеивание со с.к.о. 2 м. Систематические ошибки равны нулю.
Требуется найти параметры закона распределения суммарной ошибки, вызванной всеми перечисленными факторами.
Решение. Выбираем систему координат с горизонтальной осью 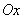 и вертикальной
и вертикальной 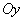 . Эти оси являются главными осями рассеивания для всех законов, кроме третьего (ошибки вследствие неточности определения дальности). Обозначим составляющие каждой ошибки в системе координат
. Эти оси являются главными осями рассеивания для всех законов, кроме третьего (ошибки вследствие неточности определения дальности). Обозначим составляющие каждой ошибки в системе координат 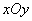 соответственно:
соответственно:
 .
.
Параметры этих составляющих равны соответственно:
 ;
;
 ;
; 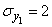 ;
; 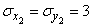 ;
;  .
.
Что касается величин 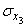 и
и 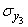 , то их мы определяем, проектируя случайную точку
, то их мы определяем, проектируя случайную точку 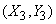 на оси
на оси 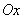 и
и 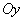 по формулам (12.8.4):
по формулам (12.8.4):
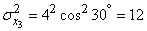 ;
;
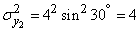 .
.
Коэффициент корреляции величин 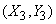 найдем по формуле (12.8.5)
найдем по формуле (12.8.5)
 ,
,
что и естественно, так как рассеивание сосредоточено на одной прямой и, следовательно, величины 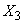 и
и  зависимы функционально.
зависимы функционально.
Применяя теорему сложения дисперсий, имеем:
 ;
; 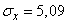 (м);
(м);
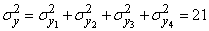 ;
;  (м).
(м).
Коэффициент корреляции  найдем, применяя теорему сложения корреляционных моментов:
найдем, применяя теорему сложения корреляционных моментов:
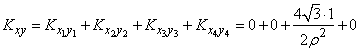 ,
,
откуда
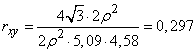 .
.
Определим угол 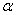 , который составляет с осью первая главная ось рассеивания:
, который составляет с осью первая главная ось рассеивания:
 ,
,
 ;
; 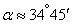 .
.
По формулам (12.8.8) имеем:
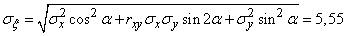 (м);
(м);
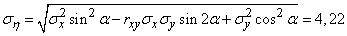 (м).
(м).
Информация, изложенная в данной статье про композиция нормальных законов на плоскости , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое композиция нормальных законов на плоскости и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про композиция нормальных законов на плоскости
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ