Случайные события Алгебра событий Классическое и статистическое определения вероятности события

Привет, сегодня поговорим про случайные события алгебра событий классическое, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое случайные события алгебра событий классическое, статистическое определения вероятности события , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В экономике, так же как и в других областях человеческой деятельности или в природе, постоянно приходится иметь дело с событиями, которые невозможно точно предсказать. Так, объем продаж товара зависит от спроса, который может существенно изменяться, и от ряда других факторов, которые учесть практически нереально. Поэтому при организации производства и осуществлении продаж приходится прогнозировать исход такой деятельности на основе либо собственного предыдущего опыта, либо аналогичного опыта других людей, либо интуиции, которая в значительной степени тоже опирается на опытные данные.

Чтобы каким-то образом оценить рассматриваемое событие, необходимо учитывать или специально организовывать условия, в которых фиксируется это событие.

Осуществление определенных условий или действий для выявления рассматриваемого события носит название опыта илиэксперимента.

Событие называется случайным, если в результате опыта оно может произойти или не произойти.

Событие называется достоверным, если оно обязательно появляется в результате данного опыта, и невозможным, если оно не может появиться в этом опыте.

Например, выпадение снега в Москве 30 ноября является случайным событием. Ежедневный восход Солнца можно считать достоверным событием. Выпадение снега на экваторе можно рассматривать как невозможное событие.

Одной из главных задач в теории вероятностей является задача определения количественной меры возможности появления события.

Алгебра событий

Суммой событий 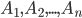 называется событие, состоящее в появлении хотя бы одного из этих событий

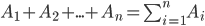
В качестве примера суммы событий можно назвать наличие в магазине хотя бы одного из двух товаров.

Произведением событий 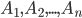называется событие, состоящее в одновременном появлении всех этих событий

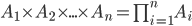
Событие, состоящее в появлении одновременно в магазине двух товаров является произведением событий: 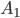 -появление одного товара, —  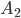появление другого товара.

События 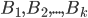 образуют полную группу событий, если хотя бы одно из них обязательно произойдет в опыте.

Пример. В порту имеется два причала для приема судов. Можно рассмотреть три события:  — отсутствие судов у причалов, 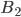 — присутствие одного судна у одного из причалов,  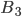— присутствие двух судов у двух причалов. Эти три события образуют полную группу событий.

Противоположными называются два единственно возможных события, образующих полную группу.

Если одно из событий, являющихся противоположными, обозначить через , то противоположное событие обычно обозначают через .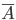

Классическое и статистическое определения вероятности события

Каждый из равновозможных результатов испытаний (опытов) называется элементарным исходом. Об этом говорит сайт https://intellect.icu . Их обычно обозначают буквами 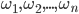. Например, бросается игральная кость. Элементарных исходов всего может быть шесть по числу очков на гранях.

Из элементарных исходов можно составить более сложное событие. Так, событие выпадения четного числа очков определяется тремя исходами: 2, 4, 6.

Количественной мерой возможности появления рассматриваемого события является вероятность.

Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.

Классическое определение вероятности связано с понятием благоприятствующего исхода.

Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события.

В приведенном примере рассматриваемое событие — четное число очков на выпавшей грани, имеет три благоприятствующих исхода. В данном случае известно и общее 
количество возможных исходов. Значит, здесь можно использовать классическое определение вероятности события.

Классическое определение. Вероятность события равняется отношению числа благоприятствующих исходов к общему числу возможных исходов

 (1.1)

где 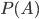 — вероятность события ,  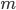— число благоприятствующих событию исходов, 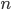 — общее число возможных исходов.

В рассмотренном примере

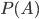= 3/6= 0.5

Статистическое определение вероятности связано с понятием относительной частоты появления события в опытах.

Относительная частота появления события  вычисляется по формуле

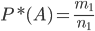(1.2)

где m1 - число появления события в серии из n1 опытов (испытаний).

Статистическое определение. Вероятностью события  называется число, относительно которого стабилизируется (устанавливается) относительная частота 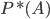 при неограниченном увеличении числа опытов.

В практических задачах за вероятность события  принимается относительная частота 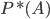 при достаточно большом числе испытаний.

Из данных определений вероятности события  видно, что всегда выполняется неравенство

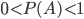
Для определения вероятности события на основе формулы (1.1) часто используются формулы комбинаторики, по которым находится число благоприятствующих исходов и общее число возможных исходов.

Пример. Известно, что в поступившей партии из 30 швейных машинок 10 имеют внутренний дефект. Определить вероятность того, что из партии в 5 наудачу взятых машинок 3 окажутся бездефектными.

Решение. Для решения данной задачи введем обозначения. Пусть 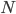 — общее число машинок,  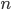— число бездефектных машинок,  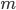— число отобранных в партию машинок,  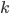— число бездефектных машинок в отобранной партии.

Общее число комбинаций по 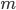 машинок, т.е. общее число возможных исходов будет равно числу сочетаний из  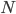элементов по 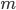, т.е. 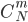. Но в каждой отобранной комбинации должно содержаться по три бездефектные машинки. Число таких комбинаций равно числу сочетаний из  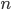элементов по 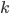, т.е. .

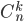С каждой такой комбинацией в отобранной партии оставшиеся дефектные элементы тоже образуют множество комбинаций, число которых равно числу сочетаний из N-n  элементов по m-k , т.е. .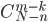

Это значит, что общее число благоприятствующих исходов определяется произведением 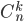. Откуда получаем

=     /  

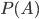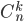
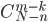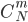
Подставим в эту формулу численные значения данного примера

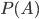 = (C2 0^3  * C1 0^2 ) / C3 0^5  

Надеюсь, эта статья про случайные события алгебра событий классическое, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое случайные события алгебра событий классическое, статистическое определения вероятности события и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ