Лекция
Привет, Вы узнаете о том , что такое генеральная совокупность, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое генеральная совокупность, выборочный метод, ошибки выборки, объем выборки , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Статистическая совокупность - множество единиц, обладающих массовостью, типичностью, качественной однородностью и наличием вариации.Статистическая совокупность состоит из материально существующих объектов (Работники, предприятия, страны, регионы), является объектом статистического исследования.
Единица совокупности — каждая конкретная единица статистической совокупности.Одна и таже статистическая совокупность может быть однородна по одному признаку и неоднородна по другому.
Качественная однородность — сходство всех единиц совокупности по какому-либо признаку и несходство по всем остальным.В статистической совокупности отличия одной единицы совокупности от другой чаще имеют количественную природу. Количественные изменения значений признака разных единиц совокупности называются вариацией.
Вариация признака — количественное изменение признака (для количественного признака) при переходе от одной единицы совокупности к другой.
Признак - это свойство, характерная черта или иная особенность единиц, объектов и явлений, которая может быть наблюдаема или измерена. Признаки делятся на количественные и качественные. Многообразие и изменчивость величины признака у отдельных единиц совокупности называется вариацией.
Атрибутивные (качественные) признаки не поддаются числовому выражению (состав населения по полу). Количественные признаки имеют числовое выражение (состав населения по возрасту).
Показатель — это обобщающая количественно качестванная характеристика какого-либо свойства единиц или совокупности в цельм в конкретных условиях времени и места.
Система показателей — это совокупность показателей всесторонне отражающих изучаемое явление.
Например, изучается зарплата:
Основу статистического исследования составляет множество данных, полученных в результате измерения одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений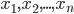 
случайной величины 
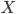, является выборкой, а гипотетически существующая (домысливаемая) — генеральной совокупностью. Генеральная совокупность может быть конечной (число наблюдений N = const) или бесконечной (N = ∞), а выборка из генеральной совокупности — это всегда результат ограниченного ряда 
наблюдений. Число наблюдений , образующих выборку, называется объемом выборки. Если
объем выборки достаточно велик (n → ∞) выборка считается большой, в противном случае она называется выборкой ограниченного объема. Выборка считается малой, если при измерении одномерной случайной величины 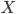объем выборки не превышает 30 (n <= 30), а при измерении одновременно нескольких (k) признаков в многомерном пространстве отношение n к k не превышает 10 (n/k < 10). Выборка образует вариационный ряд, если ее члены являются порядковыми статистиками, т. е. выборочные значения случайной величины Х упорядочены по возрастанию (ранжированы), значения же признака называются вариантами.
Пример. Практически одна и та же случайно отобранная совокупность объектов — коммерческих банков одного административного округа Москвы, может рассматриваться как выборка из генеральной совокупности всех коммерческих банков этого округа, и как выборка из генеральной совокупности всех коммерческих банков Москвы, а также как выборка из коммерческих банков страны и т.д.
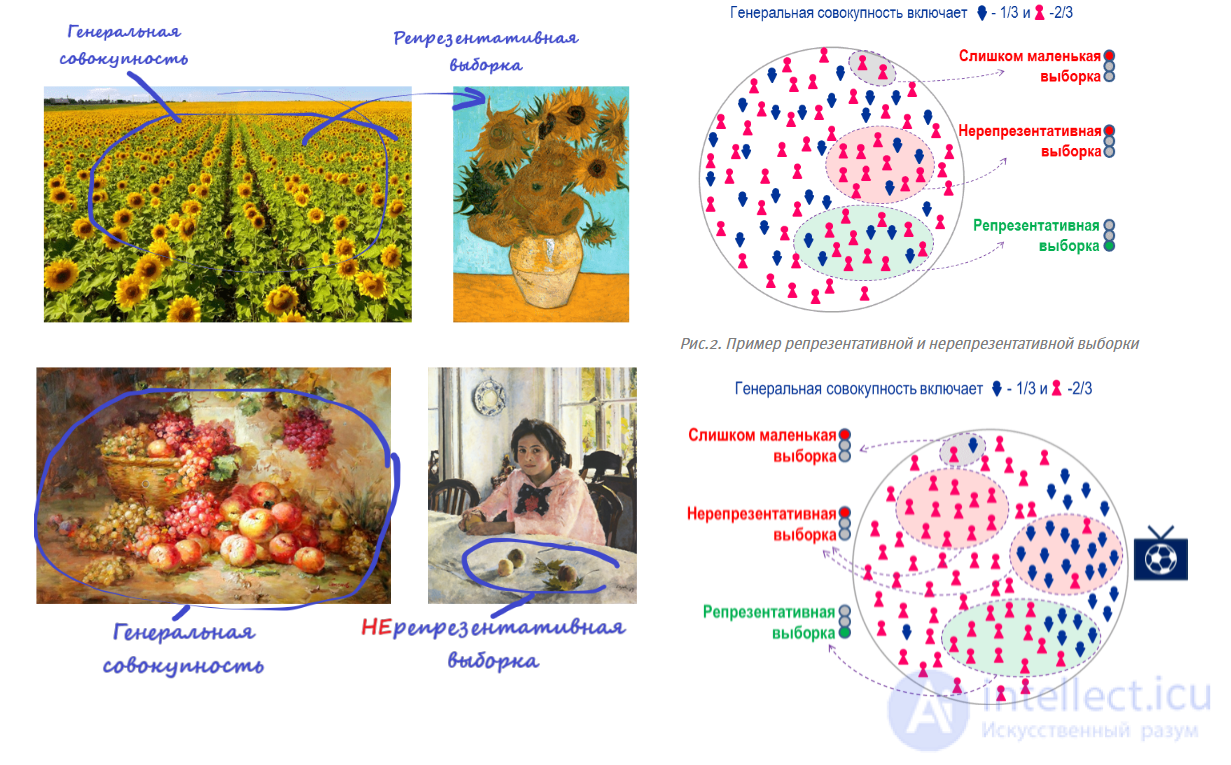
Достоверность статистических выводов и содержательная интерпретация результатов зависит от репрезентативности выборки, т.е. полноты и адекватности представления свойств генеральной совокупности, по отношению к которой эту выборку можно считать представительной. Изучение статистических свойств совокупности можно организовать двумя способами: с помощью сплошного и несплошного наблюдения . Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности, а несплошное (выборочное) наблюдение — только его части.
Существуют пять основных способов организации выборочного наблюдения:
1. простой случайный отбор, при котором объектов случайно извлекаются из генеральной совокупности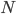 
объектов (например с помощью таблицы или датчика случайных чисел), причем каждая из возможных выборок имеют равную вероятность. Такие выборки называются собственно-случайными;
2. простой отбор с помощью регулярной процедуры осуществляется с помощью механической составляющей (например, даты, дня недели, номера квартиры, буквы алфавита и др.) и полученные таким способом выборки называются механическими;
3. стратифицированный отбор заключается в том, что генеральная совокупность объема 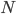подразделяется на подсовокупности или слои (страты) объема 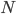так что 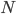. Страты представляют собой однородные объекты с точки зрения статистических характеристик (например, население делится на страты по возрастным группам или социальной принадлежности; предприятия — по отраслям). В этом случае выборки называются стратифицированными (иначе, расслоенными, типическими, районированными);
4. методы серийного отбора используются для формирования серийных или гнездовых выборок. Они удобны в том случае, если необходимо обследовать сразу "блок" или серию объектов (например, партию товара, продукцию определенной серии или население при территориально-административном делении страны). Отбор серий можно осуществить собственно-случайным или механическим способом. При этом проводится сплошное обследование определенной партии товара, или целой территориальной единицы (жилого дома или квартала);
5. комбинированный (ступенчатый ) отбор может сочетать в себе сразу несколько способов отбора (например, стратифицированный и случайный или случайный и механический); такая выборка называется комбинированной.
Виды отбора
По виду различаются индивидуальный, групповой и комбинированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом отборе — качественно однородные группы (серии) единиц, а комбинированный отбор предполагает сочетание первого и второго видов.
По методу отбора различают повторную и бесповторную выборку.
Бесповторным называется отбор, при котором попавшая в выборку единица не возвращается в исходную совокупность и в дальнейшем выборе не участвует; при этом численность единиц генеральной совокупности N сокращается в процессе отбора. При повторном отборе попавшая в выборку единица после регистрации возвращается в генеральную совокупность и таким образом сохраняет равную возможность наряду с другими единицами быть использованной в дальнейшей процедуре отбора; при этом численность единиц генеральной совокупности N остается неизменной (метод в социально-экономических исследованиях применяется редко). Однако, при большом N (N → ∞) формулы для бесповторного отбора приближаются к аналогичным для повторного отбора и практически чаще используются последние (N = const).
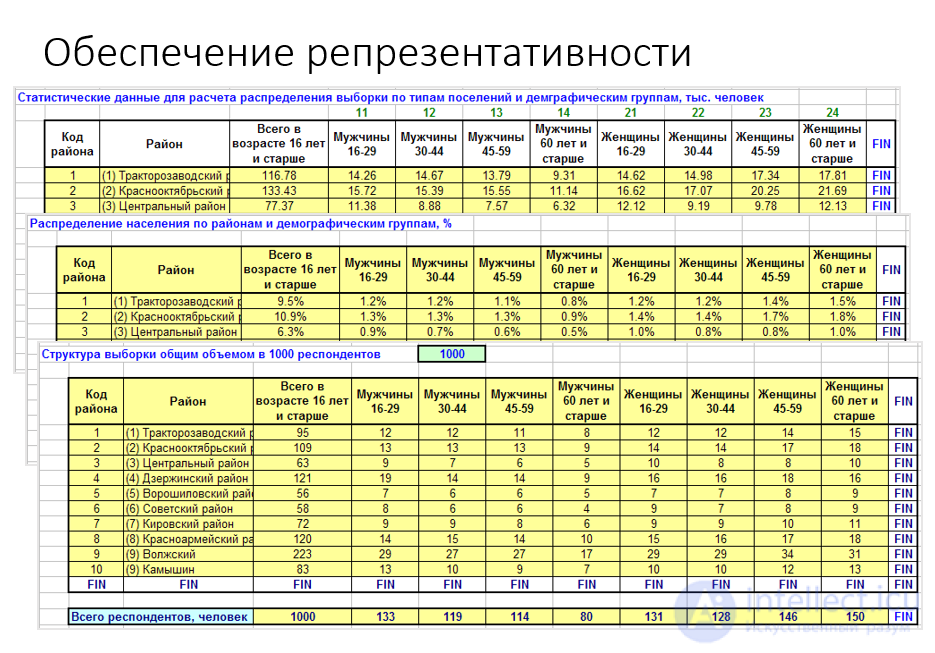
рис. Обеспечение репрезентативности
Для репрезентативной выборки выборочное распределение должно соответствовать генеральной совокупности по основным контролируемым признакам (в данном случае – район проживания, пол и возраст)
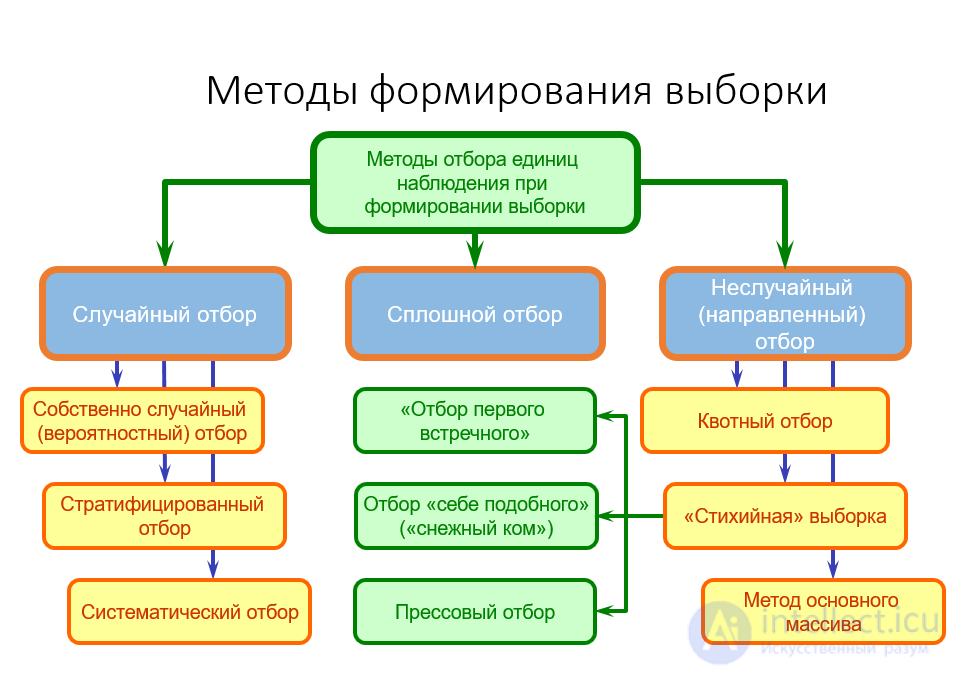
Рис. Методы формирования выборки
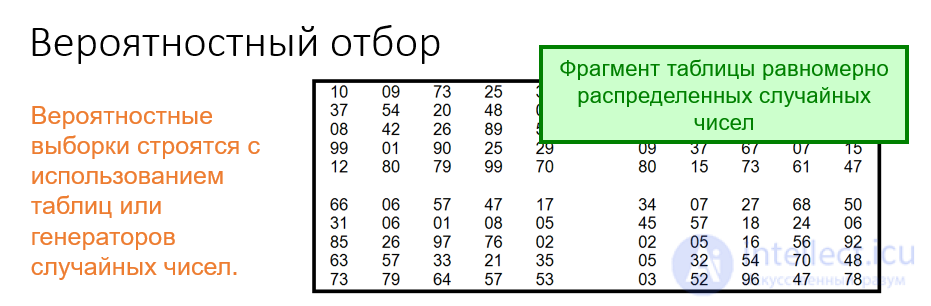
Рис. Вероятностный отбор
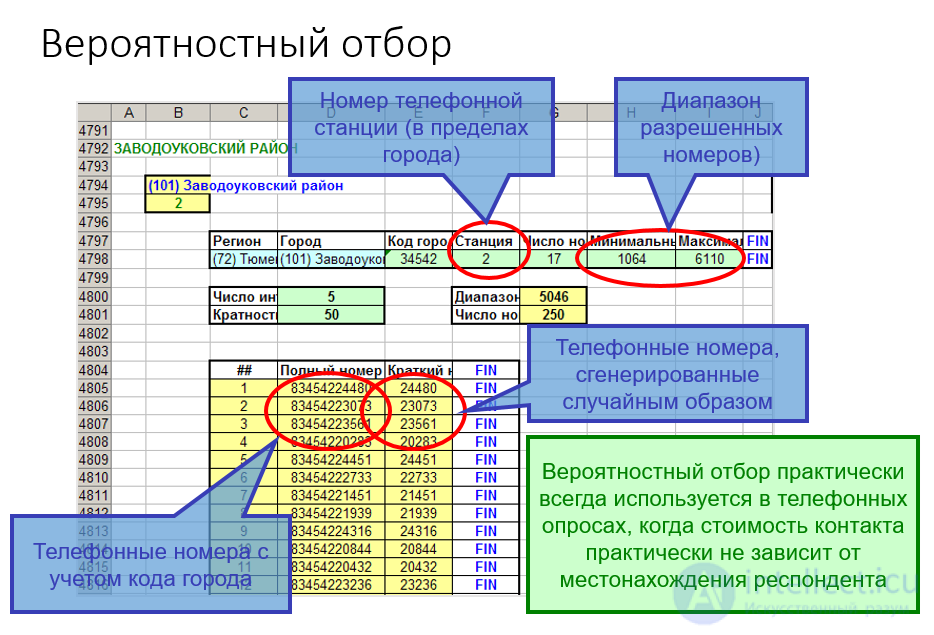
Рис. Вероятностный отбор
Систематический отбор
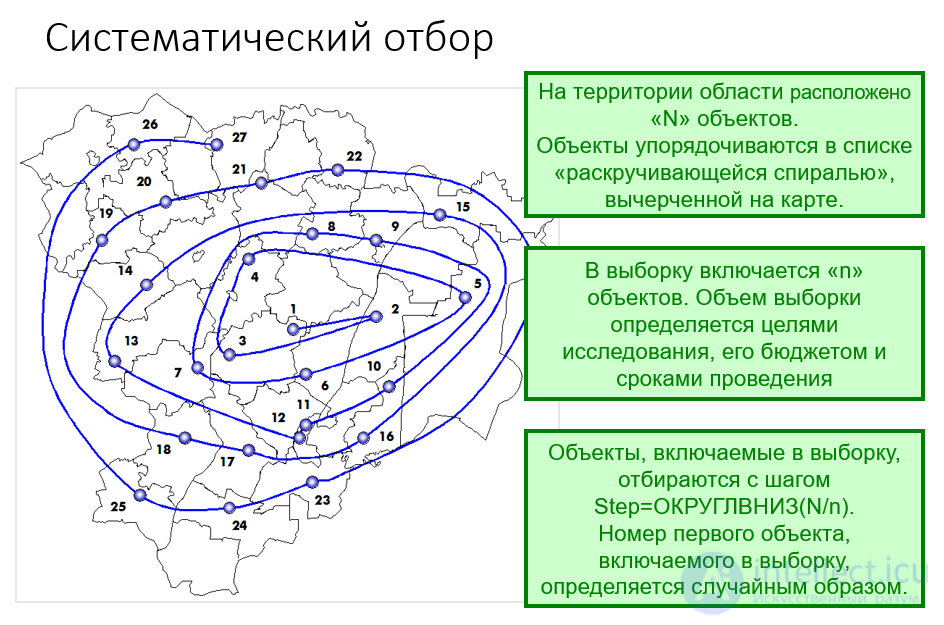
Стратифицированный отбор
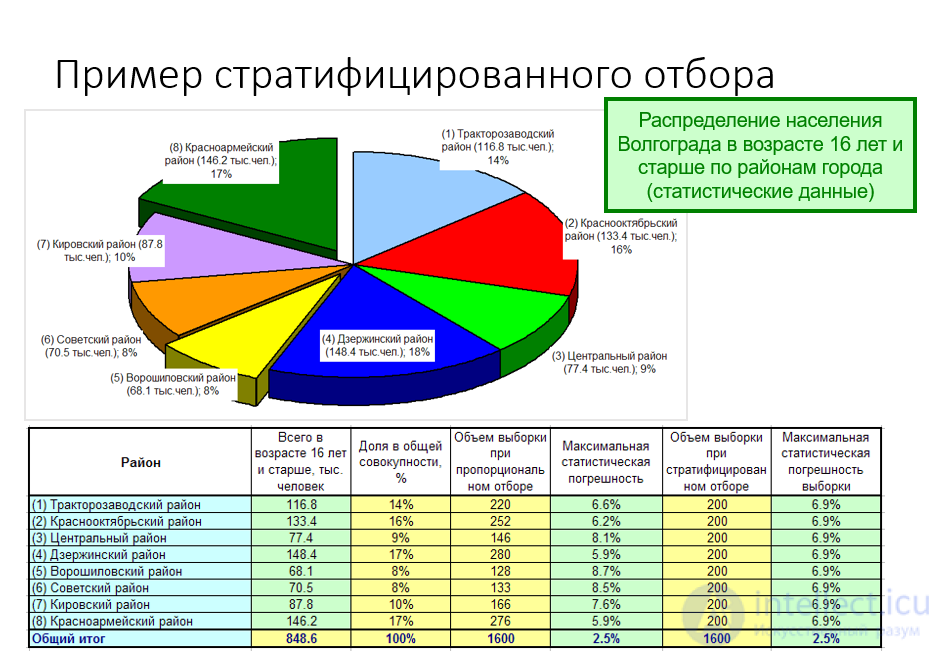
Рис. Об этом говорит сайт https://intellect.icu . Пример стратифицированного отбора
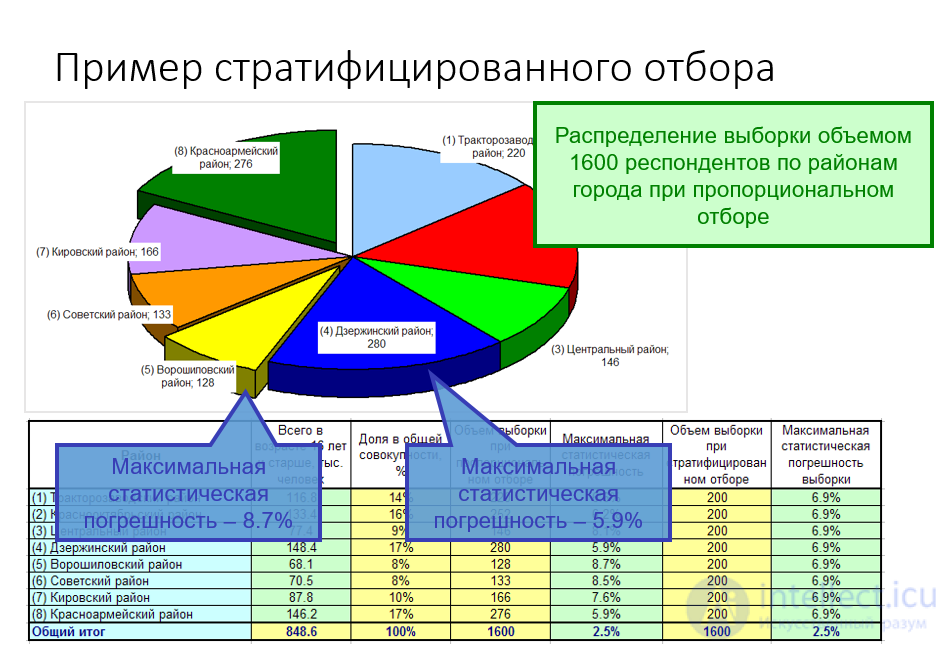
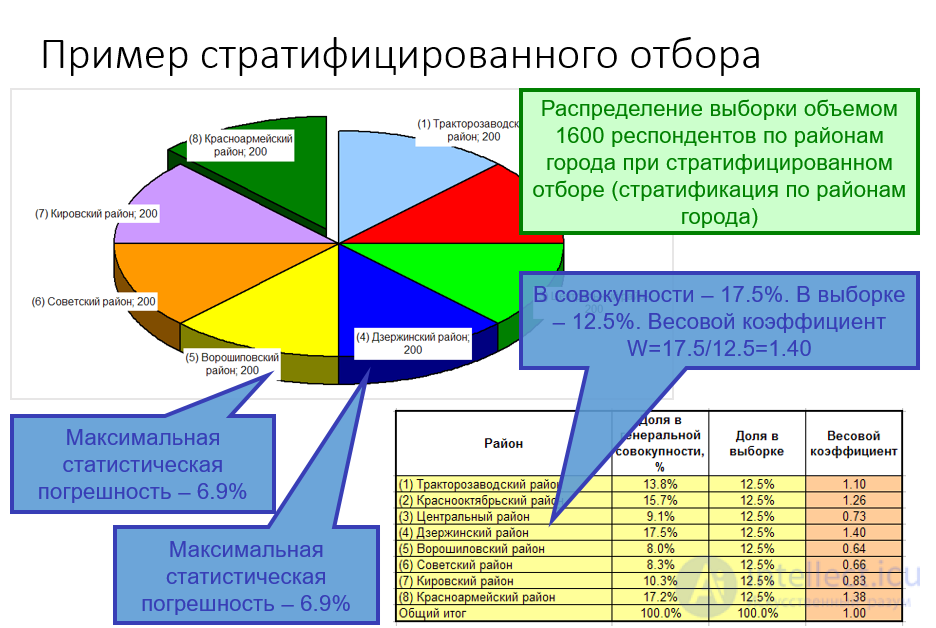
Направленный отбор
В основе статистических выводов проведенного исследования лежит распределение случайной величины 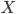, наблюдаемые же значения (х1, х2, … , хn) называются реализациями случайной величины Х (n — объем выборки). Распределение случайной величины 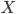в генеральной совокупности носит теоретический, идеальный характер, а ее выборочный аналог является эмпирическим распределением. Некоторые теоретические распределения заданы аналитически, т.е. их параметры определяют значение функции распределения 
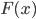в каждой точке пространства возможных значений случайной величины 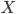. Для выборки же функцию распределения определить трудно, а иногда невозможно, поэтому параметры оценивают по эмпирическим данным, а затем их подставляют в аналитическое выражение, описывающее теоретическое распределение. При этом предположение (или гипотеза) о виде распределения может быть как статистически верным, так и ошибочным. Но в любом случае восстановленное по выборке эмпирическое распределение лишь грубо характеризует истинное. Важнейшими параметрами распределений являются математическое ожидание 
и дисперсия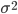 
.
По своей природе распределения бывают непрерывными и дискретными. Наиболее известным непрерывным распределением является нормальное. Выборочными аналогами параметров и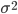для него являются: среднее значение 
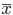и эмпирическая дисперсия 
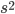. Среди дискретных в социально-экономических исследованиях наиболее часто применяется альтернативное (дихотомическое) распределение. Параметр математического ожидания этого распределения выражает относительную величину (или долю) единиц совокупности, которые обладают изучаемым признаком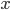 
(она обозначена буквой 
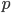); доля совокупности, не обладающая этим признаком, обозначается буквой q (q = 1 — p). Дисперсия же 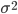альтернативного распределения также имеет эмпирический аналог .
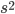В зависимости от вида распределения и от способа отбора единиц совокупности по-разному вычисляются характеристики параметров распределения. Основные из них для теоретического и эмпирического распределений приведены в табл. 9.1.
Долей выборки kn называется отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:
kn = n/N.
Выборочная доля w — это отношение единиц, обладающих изучаемым признаком x к объему выборки n:
w = nn/n.
Пример. В партии товара, содержащей 1000 ед., при 5% выборке доля выборки kn в абсолютной величине составляет 50 ед. (n = N*0,05); если же в этой выборке обнаружено 2 бракованных изделия, то выборочная доля брака w составит 0,04 (w = 2/50 = 0,04 или 4%).
Так как выборочная совокупность отлична от генеральной, то возникают ошибки выборки .
Таблица 9.1 Основные параметры генеральной и выборочной совокупностей
При любом статистическом наблюдении (сплошном и выборочном) могут встретиться ошибки двух видов: регистрации и репрезентативности. Ошибки регистрации могут иметь случайный и систематический характер. Случайные ошибки складываются из множества различных неконтролируемых причин, носят непреднамеренный характер и обычно по совокупности уравновешивают друг друга (например, изменения показателей прибора при температурных колебаниях в помещении).
Систематические ошибки тенденциозны, так как нарушают правила отбора объектов в выборку (например, отклонения в измерениях при изменении настройки измерительного прибора).
Пример. Для оценки социального положения населения в городе предусмотрено обследовать 25% семей. Если при этом выбор каждой четвертой квартиры основан на ее номере, то существует опасность отобрать все квартиры только одного типа (например, однокомнатные), что обеспечит систематическую ошибку и исказит результаты; выбор же номера квартиры по жребию более предпочтителен, так как ошибка будет случайной.
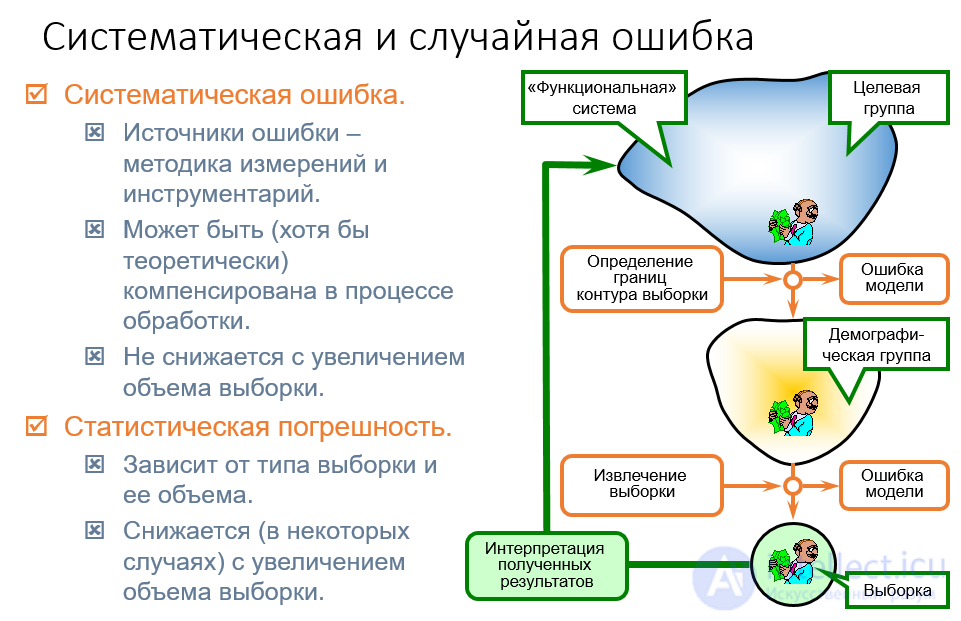
Рис. Систематическая и случайная ошибка
Ошибки репрезентативности присущи только выборочному наблюдению, их невозможно избежать и они возникают в результате того, что выборочная совокупность не полностью воспроизводит генеральную. Значения показателей, получаемых по выборке, отличаются от показателей этих же величин в генеральной совокупности (или получаемых при сплошном наблюдении).
Ошибка выборочного наблюдения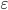 
есть разность между значением параметра в генеральной совокупности и ее выборочным значением. Для среднего значения количественного признака она равна: 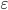, а для доли (альтернативного признака) — .
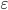Ошибки выборки свойственны только выборочным наблюдениям. Чем больше эти ошибки, тем больше эмпирическое распределение отличается от теоретического. Параметры эмпирического распределения 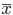и 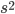являются случайными величинами, следовательно, ошибки выборки также являются случайными величинами, могут принимать для разных выборок разные значения и поэтому принято вычислять среднюю ошибку.
Средняя ошибка выборки есть величина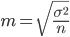 
, выражающая среднее квадратическое отклонение выборочной средней от математического ожидания. Эта величина при соблюдении принципа случайного отбора зависит прежде всего от объема выборки и от степени варьирования признака: чем больше и чем меньше вариация признака (следовательно, и значение 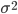), тем меньше величина средней ошибки выборки 
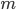. Соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой:
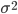
т.е. при достаточно больших можно считать, что 
. Средняя ошибка выборки показывает возможные отклонения параметра выборочной совокупности от параметра генеральной. В табл. 9.2 приведены выражения для вычисления средней ошибки 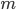выборки при разных методах организации наблюдения.
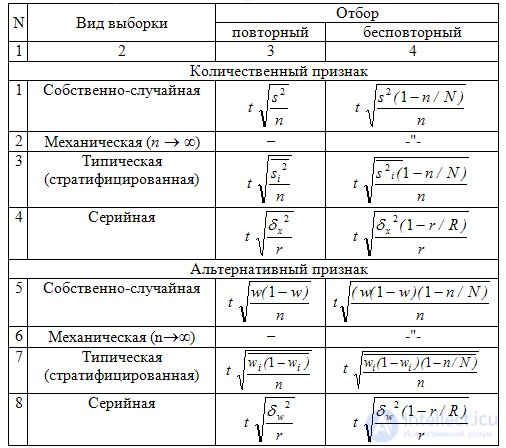
Таблица 9.2 Средняя ошибка (m) выборочных средней и доли для разных видов выборки
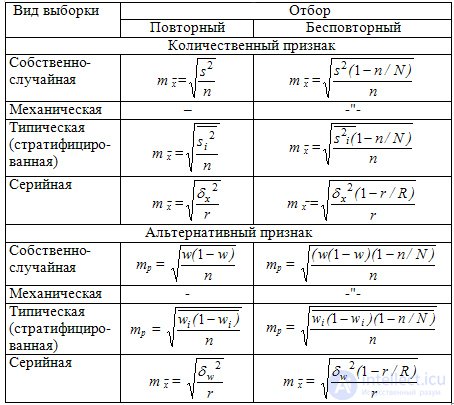
Где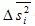 
- средняя из внутригрупповых выборочных дисперсий для непрерывного признака;
- средняя из внутригрупповых дисперсий доли;
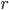— число отобранных серий, 
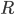— общее число серий;
,
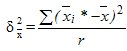где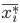 
— средняя 
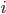-й серии;
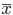— общая средняя по всей выборочной совокупности для непрерывного признака;
,
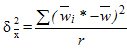где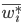 
— доля признака в 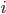-й серии;
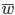— общая доля признака по всей выборочной совокупности.
Однако о величине средней ошибки 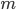можно судить лишь с определенной, вероятностью Р (Р ≤ 1). Ляпунов А.М. доказал, что распределение выборочных средних 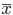, a следовательно, и их отклонений от генеральной средней, при достаточно большом числе приближенно подчиняется нормальному закону распределения при условии, что генеральная совокупность обладает конечной средней и ограниченной дисперсией.
Математически это утверждение для средней выражается в виде:
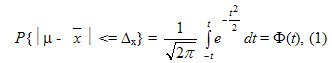
а для доли выражение (1) примет вид:
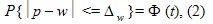
где 
- есть предельная ошибка выборки, которая кратна величине средней ошибки выборки 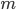, а коэффициент кратности 
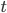— есть критерий Стьюдента ("коэффициент доверия"), предложенный У.С. Госсетом (псевдоним "Student"); значения 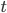для разного объема выборки хранятся в специальной таблице.
Значения функции Ф(t) при некоторых значениях t равны:
Следовательно, выражение (3) может быть прочитано так: с вероятностью Р = 0,683 (68,3%) можно утверждать, что разность между выборочной и генеральной средней не превысит одной величины средней ошибки m (t = 1), с вероятностью Р = 0,954 (95,4%) — что она не превысит величины двух средних ошибок m (t = 2) , с вероятностью Р = 0,997 (99,7%) — не превысит трех значений m (t = 3) . Таким образом, вероятность того, что эта разность превысит трехкратную величину средней ошибки определяет уровень ошибки и составляет не более 0,3%.
В табл. 9.3 приведены формулы для вычисления предельной ошибки выборки.
Таблица 9.3 Предельная ошибка (D) выборки для средней и доли (р) для разных видов выборочного наблюдения
Конечной целью выборочного наблюдения является характеристика генеральной совокупности. При малых объемах выборки эмпирические оценки параметров (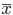 и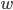 
) могут существенно отклоняться от их истинных значений ( и 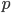). Поэтому возникает необходимость установить границы, в пределах которых для выборочных значений параметров ( 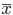и 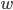) лежат истинные значения ( и ).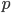
Доверительным интервалом какого-либо параметра θгенеральной совокупности называется случайная область значений этого параметра, которая с вероятностью близкой к 1 (надежностью) содержит истинное значение этого параметра.
Предельная ошибка выборки Δпозволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы, которые равны:
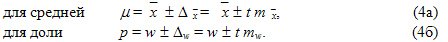
Нижняя граница доверительного интервала получена путем вычитания предельной ошибки из выборочного среднего (доли), а верхняя — путем ее добавления.
Доверительный интервал для средней использует предельную ошибку выборки и для заданного уровня достоверности 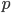определяется по формуле:
Это означает, что с заданной вероятностью Р, которая называется доверительным уровнем и однозначно определяется значением t, можно утверждать, что истинное значение средней лежит в пределах от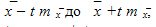 
,а истинное значение доли 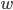— в пределах от
При расчете доверительного интервала для трех стандартных доверительных уровней Р = 95%, Р = 99% и Р = 99,9% значение 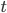выбирается по таблице Стьюдента. Приложения в зависимости от числа степеней свободы 
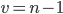. Если объем выборки достаточно велик, то соответствующие этим вероятностям значения t равны: 1,96, 2,58 и 3,29. Таким образом, предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:
Распространение результатов выборочного наблюдения на генеральную совокупность в социально-экономических исследованиях имеет свои особенности, так как требует полноты представительности всех ее типов и групп. Основой для возможности такого распространения является расчет относительной ошибки:
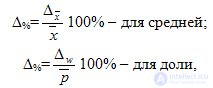
где Δ%- относительная предельная ошибка выборки; ,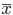 
.
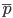Существуют два основных метода распространения выборочного наблюдения на генеральную совокупность: прямой пересчет и способ коэффициентов.
Сущность прямого пересчета заключается в умножении выборочного среднего значения !!\overline{x} на объем генеральной совокупности .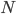
Пример. Пусть среднее число детей ясельного возраста в городе оценено выборочным методом и составило 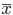человека. Если в городе 1000 молодых семей, то число необходимых мест в муниципальных детских яслях получают умножением этой средней на численность генеральной совокупности N = 1000, т.е. составит 1200 мест.
Способ коэффициентов целесообразно использовать в случае, когда выборочное наблюдение проводится с целью уточнения данных сплошного наблюдения.
При этом используют формулу:
,
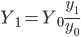где все переменные — это численность совокупности:
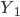— с поправкой на недоучет,
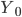- без этой поправки,
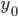— в контрольных точках
— в тех же точках по данным контрольных мероприятий.
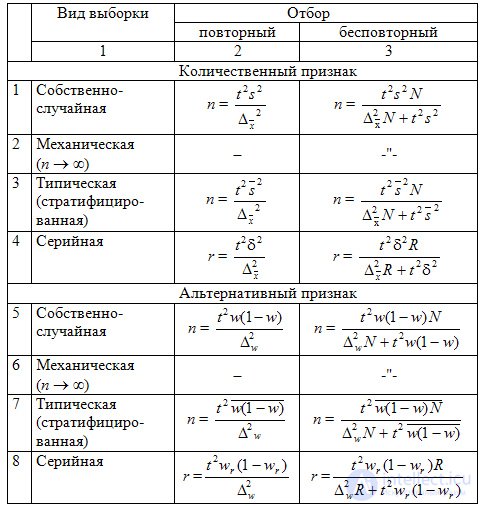
Таблица 9.4 Необходимый объем (n) выборки для разных видов организации выборочного наблюдения
При планировании выборочного наблюдения с заранее заданным значением допустимой ошибки выборки необходимо правильно оценить требуемый объем выборки. Этот объем может быть определен на основе допустимой ошибки при выборочном наблюдении исходя из заданной вероятности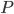 
, гарантирующей допустимую величину уровня ошибки (с учетом способа организации наблюдения). Формулы для определения необходимой численности выборки n легко получить непосредственно из формул предельной ошибки выборки. Так, из выражения для предельной ошибки:
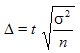
непосредственно определяется объем выборки n:
Эта формула показывает, что с уменьшением предельной ошибки выборки Δсущественно увеличивается требуемый объем выборки , который пропорционален дисперсии 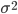и квадрату критерия Стьюдента .
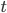Для конкретного способа организации наблюдения требуемый объем выборки вычисляется согласно формулам, приведенным в табл. 9.4.
Пример 1. Вычисление среднего значения и доверительного интервала для непрерывного количественного признака.
Для оценки скорости расчета с кредиторами в банке проведена случайная выборка 10 платежных документов. Их значения оказались равными (в днях): 10; 3; 15; 15; 22; 7; 8; 1; 19; 20.
Необходимо с вероятностью Р = 0,954 определить предельную ошибку Δ выборочной средней и доверительные пределы среднего времени расчетов.
Решение. Среднее значение вычисляется по формуле из табл. 9.1 для выборочной совокупности
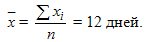
Дисперсия вычисляется по формуле из табл. 9.1.
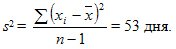
Средняя квадратическая погрешность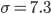 
дня.
Ошибка средней вычисляется по формуле:
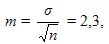
т.е. среднее значение равно x ± m = 12,0 ± 2,3 дней.
Достоверность среднего составила
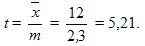
Предельную ошибку вычислим по формуле из табл. 9.3 для повторного отбора, так как численность генеральной совокупности 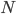неизвестна, и для Р = 0,954 уровня достоверности.
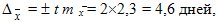
Таким образом, среднее значение равно `x ± D = `x ± 2m = 12,0 ± 4,6, т.е. его истинное значение лежит в пределах от 7,4 до16,6 дней.
Использование таблицы Стьюдента. Приложения позволяет заключить, что для n = 10 — 1 = 9 степеней свободы полученное значение достоверно с уровнем значимости a £ 0,001, т.е. полученное значение среднего достоверно отличается от 0.
Пример 2. Оценка вероятности (генеральной доли) р.
При механическом выборочном способе обследования социального положения 1000 семей выявлено, что доля малообеспеченных семей составила w = 0,3 (30%) (выборка была 2%, т.е. n/N = 0,02). Необходимо с уровнем достоверности р = 0,997 определить показатель р малообеспеченных семей во всем регионе.
Решение. По представленным значениям функции Ф(t) найдем для заданного уровня достоверности Р = 0,997 значение t = 3 (см. формулу 3). Предельную ошибку доли w определим по формуле из табл. 9.3 для бесповторного отбора (механическая выборка всегда является бесповторной):
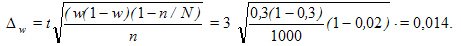
Предельная относительная ошибка выборки в % составит:
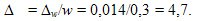
Вероятность (генеральная доля) малообеспеченных семей в регионе составит р=w±Δw, а доверительные пределы р вычисляются исходя из двойного неравенства:
w — Δw ≤ p ≤ w — Δw, т.е. истинное значение р лежит в пределах:
0,3 — 0,014 < p <0,3 + 0,014, а именно от 28,6% до 31,4%.
Таким образом, с вероятностью 0,997 можно утверждать, что доля малообеспеченных семей среди всех семей региона составляет от 28,6% до 31,4%.
Пример 3. Вычисление среднего значения и доверительного интервала для дискретного признака, заданного интервальным рядом.
В табл. 9.5. задано распределение заявок на изготовление заказов по срокам их выполнения предприятием.
Таблица 9.5 Распределение наблюдений по срокам появления
|
Срок выполнения заявок (мес.) |
Число наблюдений fi(абсолютная частота) |
Относительная частота рi (%) |
Середина интервала (градации) признака xi |
|
до 6 |
20 |
10 |
3 |
|
6-12 |
80 |
40 |
9 |
|
12-36 |
60 |
30 |
24 |
|
36-60 |
20 |
10 |
48 |
|
св.60 |
20 |
10 |
72 |
|
Всего |
200 |
100% |
|
Решение. Средний срок выполнения заявок вычисляется по формуле:
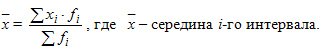
Средний срок составит:
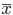= (3*20 + 9*80 + 24*60 + 48*20 + 72*20)/200 = 23,1 мес.
Тот же ответ получим, если используем данные о рi из предпоследней колонки табл. 9.5, используя формулу:
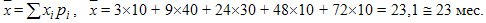
Заметим, что середина интервала для последней градации находится путем искусственного ее дополнения шириной интервала предыдущей градации равной 60 — 36 = 24 мес.
Дисперсия вычисляется по формуле
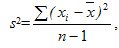
где хi- середина интервального ряда.
Следовательно !!\sigma = \frac {20^2 + 14^2 + 1 + 25^2 + 49^2}{4}, а средняя квадратическая погрешность 
.
Ошибка средней вычисляется по формуле 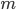мес., т.е. среднее значение равно !!\overline{x} ± m = 23,1 ± 13,4.
Предельную ошибку вычислим по формуле из табл. 9.3 для повторного отбора, так как численность генеральной совокупности 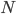неизвестна, для 0,954 уровня достоверности:
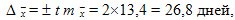
Таким образом, среднее значение равно:
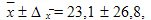
т.е. его истинное значение лежит в пределах от 0 до 50 мес.
Пример 4. Для определения скорости расчетов с кредиторами N = 500 предприятий корпорации в коммерческом банке необходимо провести выборочное исследование методом случайного бесповторного отбора. Определить необходимый объем выборки n, чтобы с вероятностью Р = 0,954 ошибка среднего значения выборки не превышала 3-х дней, если пробные оценки показали, что среднее квадратическое отклонение s составило 10 дней.
Решение. Для определения числа необходимых исследований n воспользуемся формулой для бесповторного отбора из табл. 9.4:
В ней значение t определяется из таблицы Стьюдента для уровня достоверности Р = 0,954. Оно равно 2. Среднее квадратическое значение s = 10, объем генеральной совокупности N = 500, а предельная ошибка среднего значения Δx= 3. Подставляя эти значения в формулу, получим:
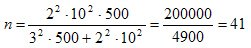
т.е. выборку достаточно составить из 41 предприятия, чтобы оценить требуемый параметр — скорость расчетов с кредиторами.
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области генеральная совокупность имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое генеральная совокупность, выборочный метод, ошибки выборки, объем выборки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ