Лекция
Привет, сегодня поговорим про распределение пуассона, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое распределение пуассона , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Функция вероятности |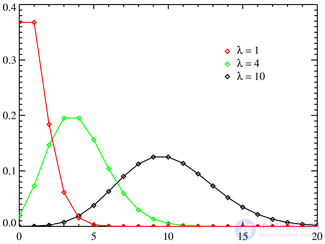
|
Функция распределения |
|
| Обозначение |  |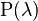
| Параметры |  |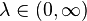
| Носитель |  |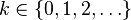
| Функция вероятности |  |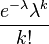
| Функция распределения |  |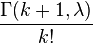
| Математическое ожидание |  |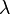
| Медиана |  |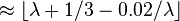
| Мода |  |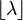
| Дисперсия | |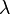
| Коэффициент асимметрии |  |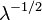
| Коэффициент эксцесса |  |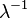
| Информационная энтропия |  |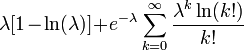
| Производящая функция моментов |  |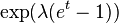
| Характеристическая функция |  |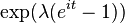
Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Выберем фиксированное число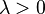 
и определим дискретное распределение, задаваемое следующейфункцией вероятности:
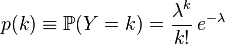,где
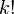обозначает факториал числа 
,
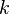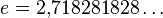— основание натурального логарифма.Тот факт , что случайная величина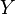 
имеет распределение Пуассона с параметром 
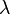, записывается: 
.
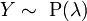Производящая функция моментов распределения Пуассона имеет вид:
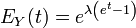,откуда
,
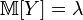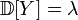.Для факториальных моментов распределения справедлива общая формула:
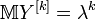,где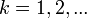 
А так как моменты и факториальные моменты линейным образом связаны, то часто для пуассоновского распределения исследуются именно факториальные моменты, из которых при необходимости можно вывести и обычные моменты.
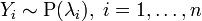. Тогда
.
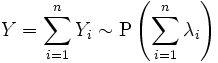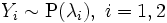, и 
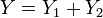. Тогда условное распределение 
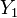при условии, что 
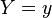, биномиально. Более точно:
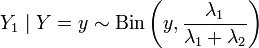.Довольно часто в теории вероятности рассматривают не само распределение Пуассона , а последовательность распределений, асимптотически равных ему. Более формально, рассматривают последовательность случайных величин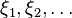 
, принимающих целочисленные значения, такую что для всякого 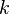выполнено 
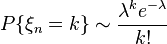при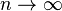 
.
Простейшим примером является случай, когда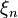 
имеет биномиальное распределение с вероятностью успеха 
в каждом из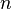 
испытаний.
Рассмотрми последовательность случайных величин 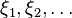, принимающих целые неотрицательные значения. Если 
при 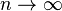и любом фиксированном 
(где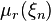 
- -ый факториальный момент), то для всякого 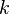при 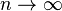выполнено .
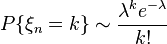Для начала докажем общую формулу вычисления вероятности появления конкретного значения случайной величины через факториальные моменты. Пусть для некоторого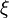 
известны все 
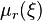и 
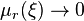при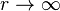 
. Тогда
Изменяя порядок суммирования, это выражение можно преобразовать в
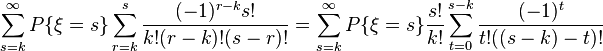
Далее, из известной формулы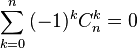 
получаем, что 
при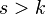 
и то же выражение вырождается в 
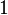при 
.
Тем самым доказано, что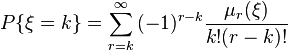 
Согласно лемме и условиям теоремы,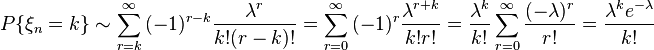 
при .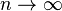
Q.E.D.
Как пример нетривиального следствия этой теоремы можно привести, например, асимптотическое стремление к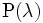 
распределения количества изолированных ребер (двухвершинных компонент связности) в случайном 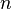-вершинном графе, где каждое из ребер включается в граф с вероятностью 
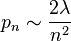.[1]
Работа Пуассона «Исследования о вероятности приговоров в уголовных и гражданских делах» опубликована в 1837 году.[2][3] Примеры других ситуаций, которые можно смоделировать, применив это распределение: поломки оборудования, длительность исполнения ремонтных работ стабильно работающим сотрудником, ошибка печати, рост колонии бактерий в чашке Петри, дефекты в длинной ленте или цепи, импульсы счетчика радиоактивного излучения и др.[4]
Надеюсь, эта статья про распределение пуассона, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое распределение пуассона и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про распределение пуассона
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ