Стандартное нормальное распределение

Привет, сегодня поговорим про стандартное нормальное распределение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое стандартное нормальное распределение , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Нормальное распределение с нулевым математическим ожиданием и единичной дисперсией называется стандартнымнормальным распределением. Вот так в данном случае выглядят плотность и функция распределения.

Правило трех сигм

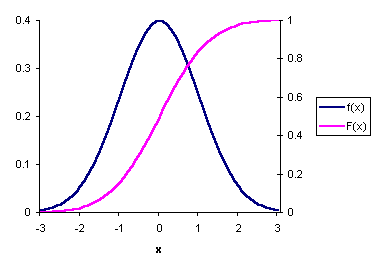
Выше значения, далекие от математического ожидания, были обозваны "аномальными". Обратите внимание, как распределение сильно "концентрируется" около одной точки.

Вероятность того, что случайное значение окажется отдалено от точки максимума более, чем на три "сигмы", очень близка к нулю, составляя примерно 0,003. Этот факт известен как правило трех сигм.

Нормальное распределение в реальном мире

Нормальное распределение или нечто близкое к нему часто имеет место в самых разных практических сферах. Об этом говорит сайт https://intellect.icu . Из-за того оно и названо нормальным. 

Применительно к социальной сфере, скажем, нормальное распределение неплохо описывает интеллект и знания населения. 80-90% народу по уровню находятся в положении "средненько", "так себе". Полные идиоты (или почти полные) находятся в суровом меньшинстве, как и очень умные люди. Это можно изобразить примерно так:

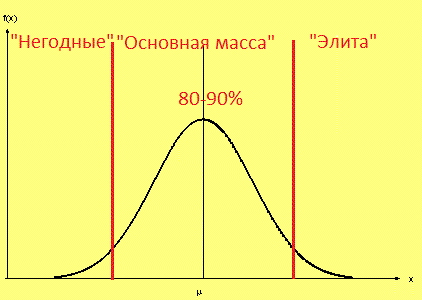
В результате прогрессивных преобразований в обществе (если такие действительно имеют место) "колокол" смещается вправо:

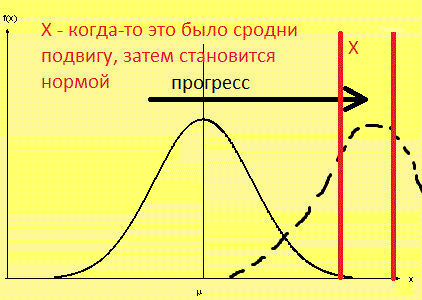
То, что когда-то считалось почти нереальным и достигалось немногими, может стать нормой. И наоборот, того, чего раньше было достаточно и на чем и останавливались почти все, теперь уже не хватает. Что получается при "откате" и губительных для общества изменениях, догадаетесь сами)

Нормальное распределение и центральная предельная теорема

Пусть ведется суммирование большого количества независимых случайных величин (или зависимых несильно) с близкими масштабами (никакое слагаемое не вносит в сумму большой вклад, отдельное слагаемое как бы не является "решающей силой"). Тогда согласно ЦПТ сумма - случайная величина, имеющая распределение, близкое к нормальному распределению. 

Только что сказанное позволяет ответить на вопрос, как можно смоделировать нормальное распределение. Берем n случайных (точнее, псевдослучайных чисел), полученных программно по обычному датчику случайных чисел, который есть в любой среде разработки. Такие датчики моделируют равномерное распределение. Каждое из n чисел должно находиться в одном диапазоне (скажем, [0; 1]). Тогда сумма из n случайных чисел и будет случайной величиной, распределение которой можно считать нормальным при достаточно большом n. Если выбирался диапазон [0; 1], то математическое ожидание составит n/2.

Надеюсь, эта статья про стандартное нормальное распределение, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое стандартное нормальное распределение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ