Экспоненциальное распределение

Привет, сегодня поговорим про экспоненциальное распределение, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое экспоненциальное распределение , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Показательное распределение

Плотность вероятности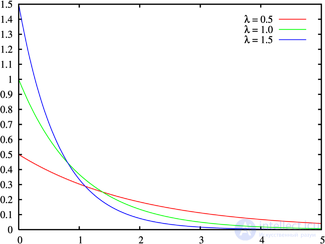
Функция распределения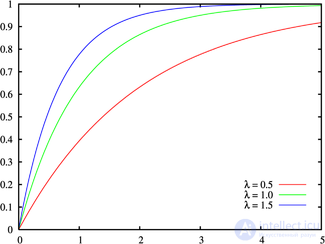
Обозначение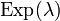
Параметры	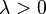- интенсивность или обратный коэффициент масштаба
Носитель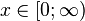
Плотность вероятности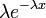
Функция распределения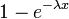
Математическое ожидание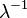
Медиана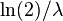
Мода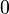
Дисперсия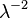
Коэффициент асимметрии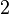
Коэффициент эксцесса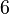
Информационная энтропия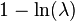
Производящая функция моментов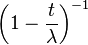
Характеристическая функция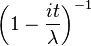

Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

Определение[править ]

Случайная величина 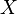 имеет экспоненциальное распределение с параметром 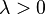, если ее плотность имеет вид

.

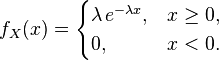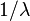Пример. Пусть есть магазин, в который время от времени заходят покупатели. Об этом говорит сайт https://intellect.icu . При определенных допущениях время между появлениями двух последовательных покупателей будет случайной величиной с экспоненциальным распределением. Среднее время ожидания нового покупателя (см. ниже) равно . Сам параметр  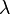тогда может быть интерпретирован как среднее число новых покупателей за единицу времени.

В этой статье для определенности будем предполагать, что плотность экспоненциальной случайной величины 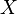задана первым уравнением, и будем писать: .

Функция распределения[править ]

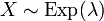Интегрируя плотность, получаем функцию экспоненциального распределения:

Моменты[править ]

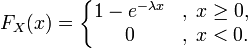
Несложным интегрированием находим, что производящая функция моментов для экспоненциального распределения имеет вид:

,

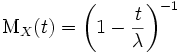откуда получаем все моменты:

.

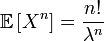В частности,

,

,

.

Отсутствие памяти[править ]

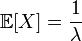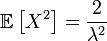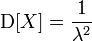Пусть 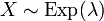. Тогда .

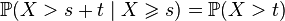Пример. Пусть автобусы приходят на остановку случайно, но с некоторой фиксированной средней интенсивностью. Тогда количество времени, уже затраченное пассажиром на ожидание автобуса, не влияет на время, которое ему еще придется прождать.

Связь с другими распределениями[править ]

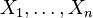• Минимум независимых экспоненциальных случайных величин также экспоненциальная случайная величина. Пусть  независимые случайные величины, и . Тогда

.

• Экспоненциальное распределение является частным случаем Гамма распределения:

.

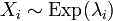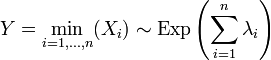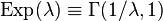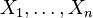• Сумма независимых одинаково распределенных экспоненциальных случайных величин имеет Гамма распределение. Пусть  независимые случайные величины, и 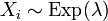. Тогда

.

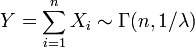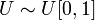• Экспоненциальное распределение может быть получено из непрерывного равномерного распределения методом обратного преобразования. Пусть . Тогда

.

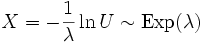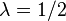• Экспоненциальное распределение с параметром  — это частный случай распределения хи-квадрат: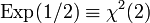

• Экспоненциальное распределение является частным случаем распределения Вейбулла.

Надеюсь, эта статья про экспоненциальное распределение, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое экспоненциальное распределение и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ