Лекция
Привет, сегодня поговорим про доверительный интервал для дисперсии нормальной выборки, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое доверительный интервал для дисперсии нормальной выборки , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Пусть  — независимая выборка из нормального распределения, где
— независимая выборка из нормального распределения, где  — известное среднее. Определим произвольное
— известное среднее. Определим произвольное 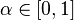 и построим
и построим  — доверительный интервал для неизвестной дисперсии
— доверительный интервал для неизвестной дисперсии 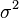 .
.
Утверждение. Случайная величина
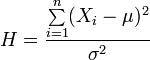
имеет распределение 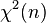 . Пусть
. Пусть 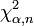 —
—  -квантиль этого распределения. Об этом говорит сайт https://intellect.icu . Тогда имеем:
-квантиль этого распределения. Об этом говорит сайт https://intellect.icu . Тогда имеем:
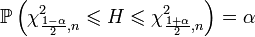 .
.После подстановки выражения для  и несложных алгебраических преобразований получаем:
и несложных алгебраических преобразований получаем:
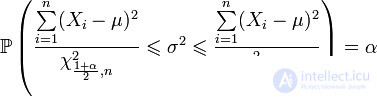 .
.Пусть  — независимая выборка из нормального распределения, где
— независимая выборка из нормального распределения, где  ,
, 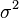 — неизвестные константы. Построим доверительный интервал для неизвестной дисперсии
— неизвестные константы. Построим доверительный интервал для неизвестной дисперсии 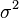 .
.
Теорема Фишера для нормальных выборок. Случайная величина
 ,
,где  — несмещенная выборочная дисперсия, имеет распределение
— несмещенная выборочная дисперсия, имеет распределение 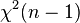 . Тогда имеем:
. Тогда имеем:
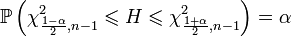 .
.После подстановки выражения для  и несложных алгебраических преобразований получаем:
и несложных алгебраических преобразований получаем:
 .
.На этом все! Теперь вы знаете все про доверительный интервал для дисперсии нормальной выборки, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое доверительный интервал для дисперсии нормальной выборки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про доверительный интервал для дисперсии нормальной выборки
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ