Плотность вероятности

Привет, сегодня поговорим про плотность вероятности, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое плотность вероятности , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Пло́тность вероя́тности — один из способов задания вероятностной меры на евклидовом пространстве 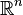. В случае, когда вероятностная мера являетсяраспределением случайной величины, говорят о плотности случайной величины.

Плотность вероятности[править ]

Пусть  является вероятностной мерой на 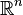, то есть определено вероятностное пространство 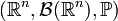, где 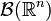 обозначает борелевскую σ-алгебру на 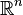. Пусть  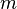обозначает меру Лебега на .

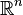Определение 1. Вероятность  называется абсолютно непрерывной (относительно меры Лебега) (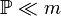), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

Если вероятность   абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция 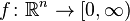 такая, что

,

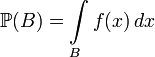где использовано общепринятое сокращение 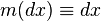, и интеграл понимается в смысле Лебега.

Определение 2. В более общем виде, пусть 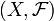 — произвольное измеримое пространство, а  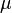и 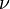 — две меры на этом пространстве. Об этом говорит сайт https://intellect.icu . Если найдется неотрицательная 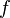, позволяющая выразить меру  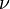через меру  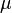в виде

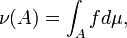
то такую функцию называют плотностью меры 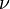 по мере 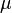, или производной Радона-Никодима меры  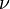относительно меры 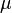, и обозначают

.

Свойства плотности вероятности[править ]

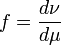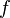• Плотность вероятности определена почти всюду. Если  является плотностью вероятности  и 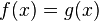 почти всюду относительно меры Лебега, то и функция также является плотностью вероятности .

• Интеграл от плотности по всему пространству равен единице:

.

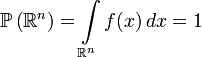Обратно, если 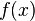 — неотрицательная п.в. функция, такая что 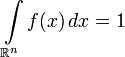, то существует абсолютно непрерывная вероятностная мера  на 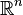 такая, что  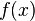является ее плотностью.

• Замена меры в интеграле Лебега:

,

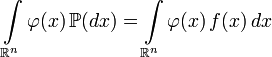где 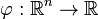 любая борелевская функция, интегрируемая относительно вероятностной меры .

Плотность случайной величины[править ]

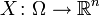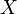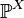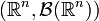Пусть определено произвольное вероятностное пространство  , и  случайная величина (или случайный вектор ).  индуцирует вероятностную меру  на , называемую распределением случайной величины .

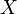Определение 3. Если распределение 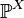 абсолютно непрерывно относительно меры Лебега, то его плотность  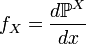называется плотностью случайной величины 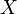. Сама случайная величина  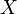называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

.

Замечания [править ]

• Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.

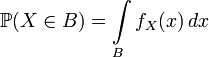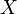• Функция распределения  абсолютно непрерывной случайной величины  непрерывна и может быть выражена через плотность следующим образом:

.

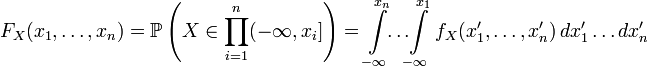В одномерном случае:

.

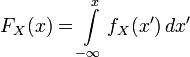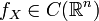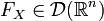Если , то , и

.

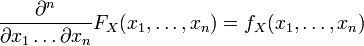В одномерном случае:

.

• Математическое ожидание  функции от абсолютно непрерывной случайной величины может быть записано в виде:

,

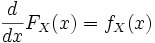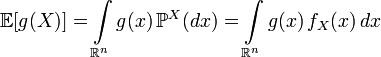где 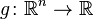 — борелевская функция, так что  определено и конечно.

Плотность преобразования случайной величины[править ]

Пусть 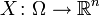 — абсолютно непрерывная случайная величина, и  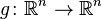— инъективная непрерывно дифференцируемая функция  такая, что 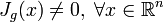, где 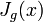 — якобиан функции  в точке 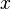. Тогда случайная величина   также абсолютно непрерывна, и ее плотность имеет вид:

.

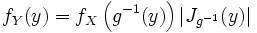В одномерном случае:

.

Примеры абсолютно непрерывных распределений[править ]

• Бета распределение;
• Распределение Вейбулла;
• Гамма распределение;
• Распределение Коши;
• Логнормальное распределение;
• Нормальное распределение;
• Непрерывное равномерное распределение
• Распределение Парето;
• Распределение Стьюдента;
• Распределение Фишера;
• Распределение хи- квадрат ;
• Экспоненциальное распределение ;
• Многомерное нормальное распределение .

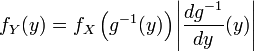Надеюсь, эта статья про плотность вероятности, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое плотность вероятности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ