8.5 Зависимые и независимые случайные величины кратко

Привет, Вы узнаете о том , что такое зависимые, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое зависимые, независимые случайные величины , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

При изучении систем случайных величин всегда следует обращать внимание на степень и характер их зависимости. Эта зависимость может быть более или менее ярко выраженной, более или менее тесной. В некоторых случаях зависимость между случайными величинами может быть настолько тесной, что, зная значение одной случайной величины, можно в точности указать значение другой. В другом крайнем случае зависимость между случайными величинами является настолько слабой и отдаленной, что их можно практически считать независимыми.

 

Понятие о независимых случайных величинах – одно их важных понятий теории вероятностей.

Случайная величина  называется независимой от случайной величины , если закон распределения величины  не зависит от того, какое значение приняла величина .

Для непрерывных случайных величин условие независимости  от  может быть записано в виде:

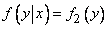
при любом .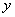

Напротив, в случае, если  зависит от , то

.

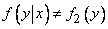Докажем, что зависимость или независимость случайных величин всегда взаимны: если величина  не зависит от .

Действительно, пусть  не зависит от :

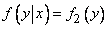.                                                            (8.5.1)

Из формул (8.4.4) и (8.4.5) имеем:

,

откуда, принимая во внимание (8.5.1), получим:

что и требовалось доказать.

Так как зависимость и независимость случайных величин всегда взаимны, можно дать новое определение независимых случайных величин.

Случайные величины  и  называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины  и  называются зависимыми.

Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид:

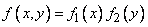,                                                              (8.5.2)

т. е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.

Условие (8.5.2) может рассматриваться как необходимое и достаточное условие независимости случайных величин.

Часто по самому виду функции 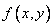 можно заключить, что случайные величины ,  являются независимыми, а именно, если плотность распределения 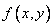 распадается на произведение двух функций, из которых одна зависит только от 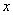, другая - только от 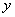, то случайные величины независимы.

Пример. Об этом говорит сайт https://intellect.icu . Плотность распределения системы  имеет вид:

.

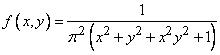Определить, зависимы или независимы случайные величины и .

Решение. Разлагая знаменатель на множители, имеем:

.

Из того, что функция 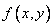 распалась на произведение двух функций, из которых одна зависима только от 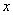, а другая  - только от 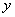, заключаем, что величины  и  должны быть независимы. Действительно, применяя формулы (8.4.2) и (8.4.3), имеем:

;

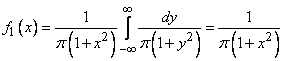аналогично

,

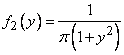откуда убеждаемся, что

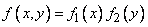
и, следовательно, величины  и  независимы.

Вышеизложенный критерий суждения о зависимости или независимости случайных величин исходит из предположения, что закон распределения системы нам известен. На практике чаще бывает наоборот: закон распределения системы  не известен; известны только законы распределения отдельных величин, входящих в систему, и имеются основания считать, что величины  и  независимы. Тогда можно написать плотность распределения системы как произведение плотностей распределения отдельных величин, входящих в систему.

Остановимся несколько подробнее на важных понятиях о «зависимости» и «независимости» случайных величин.

Понятие «независимости» случайных величин, которым мы пользуемся в теории вероятностей, несколько отличается от обычного понятия «зависимости» величин, которым мы оперируем в математике. Действительно, обычно под «зависимостью» величин подразумевают только один тип зависимости - полную, жесткую, так называемую - функциональную зависимость. Две величины  и  называются функционально зависимыми, если, зная значение одной из них, можно точно указать значение другой.

В теории вероятностей мы встречаемся с другим, более общим, типом зависимости — с вероятностной или «стохастической» зависимостью. Если величина  связана с величиной  вероятностной зависимостью, то, зная значение , нельзя указать точно значение , а можно указать только ее закон распределения, зависящий от того, какое значение приняла величина .

Вероятностная зависимость может быть более или менее тесной; по мере увеличения тесноты вероятностной зависимости она все более приближается к функциональной. Таким образом, функциональную зависимость можно рассматривать как крайний, предельный случай наиболее тесной вероятностной зависимости. Другой крайний случай - полная независимость случайных величин. Между этими двумя крайними случаями лежат все градации вероятностной зависимости - от самой сильной до самой слабой. Те физические величины, которые на практике мы считаем функционально зависимыми, в действительности связаны весьма тесной вероятностной зависимостью: при заданном значении одной из этих величин другая колеблется в столь узких пределах, что ее практически можно считать вполне определенной. С другой стороны, те величины, которые мы на практике считаем независимыми, и действительности часто находятся в некоторой взаимной зависимости, но эта зависимость настолько слаба, что ею для практических целей можно пренебречь.

Вероятностная зависимость между случайными величинами очень часто встречается на практике. Если случайные величины  и  находятся в вероятностной зависимости, это не означает, что с изменением величины  величина  изменяется вполне определенным образом; это лишь означает, что с изменением величины  величина  имеет тенденцию также изменяться (например, возрастать или убывать при возрастании ). Эта тенденция соблюдается лишь «в среднем», в общих чертах, и в каждом отдельном случае от нее возможны отступлении.

Рассмотрим, например, две такие случайные величины:  - рост наугад взятого человека,  - его вес. Очевидно, величины  и  находятся в определенной вероятностной зависимости; она выражается в том, что в общем люди с большим ростом имеют больший вес. Можно даже составить эмпирическую формулу, приближенно заменяющую эту вероятностную зависимость функциональной. Такова, например, общеизвестная формула, приближенно выражающая зависимость между ростом и весом:

.

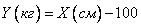Формулы подобного типа, очевидно, не являются точными и выражают лишь некоторую среднюю, массовую закономерность, тенденцию, от которой в каждом отдельном случае возможны отступления.

В вышеприведенном примере мы имели дело со случаем явно выраженной зависимости. Рассмотрим теперь такие две случайные величины:  - рост наугад взятого человека; 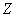 - его возраст. Очевидно, для взрослого человека величины  и 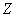 можно считать практически независимыми; напротив, для ребенка величины  и 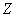 являются зависимыми.

Приведем еще несколько примеров случайных величин, находящихся в различных степенях зависимости.

1. Из камней, составляющих кучу щебня, выбирается наугад один камень. Случайная величина 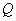 - вес камня; случайная величина  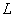- наибольшая длина камня. Величины  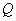и 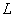 находятся в явно выраженной вероятностной зависимости.

2. Производится стрельба ракетой в заданный район океана. Величина 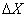 - продольная ошибка точки попадания (недолет, перелет); случайная величина  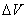- ошибка в скорости ракеты в конце активного участка движения. Величины  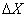и 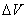 явно зависимы, так как ошибка  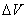является одной из главных причин, порождающих продольную ошибку .

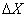3. Летательный аппарат, находясь в полете, измеряет высоту над поверхностью Земли с помощью барометрического прибора. Рассматриваются две случайные величины:  - ошибка измерения высоты и 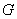 - вес топлива, сохранившегося в топливных баках к моменту измерения. Величины и 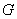 практически можно считать независимыми.

В следующем  мы познакомимся с некоторыми числовыми характеристиками системы случайных величин, которые дадут нам возможность оценивать степень зависимости этих величин.

 

Информация, изложенная в данной статье про зависимые , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое зависимые, независимые случайные величины и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про зависимые