Полигон и гистограмма примеры построения кратко

Привет, сегодня поговорим про гистограмма, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое гистограмма, полигон, пример построения полигона, пример построения гистограммы , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

Многим интересно как построить полигон относительных частот или гистограмму?

В статистике для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки 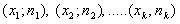. Для построения полигона частот на оси абсцисс откладывают варианты 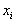, а на оси ординат – соответствующие им частоты 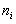и соединяют точки отрезками прямых.

Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты .

В случае непрерывного признака строится гистограмма , для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала 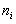– сумму частот вариант, попавших в i–й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению 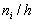. Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте) . Площадь i–го прямоугольника равна 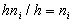– сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

В случае гистограммы относительных частот по оси ординат откладываются относительные частоты , на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте . Площадь i–го прямоугольника равна относительной частоте вариант 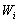, попавших в i–й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.

Для наглядности строят различные графики статистического распределения.

По данным дискретного вариационного ряда строят полигон частот или относительных частот.

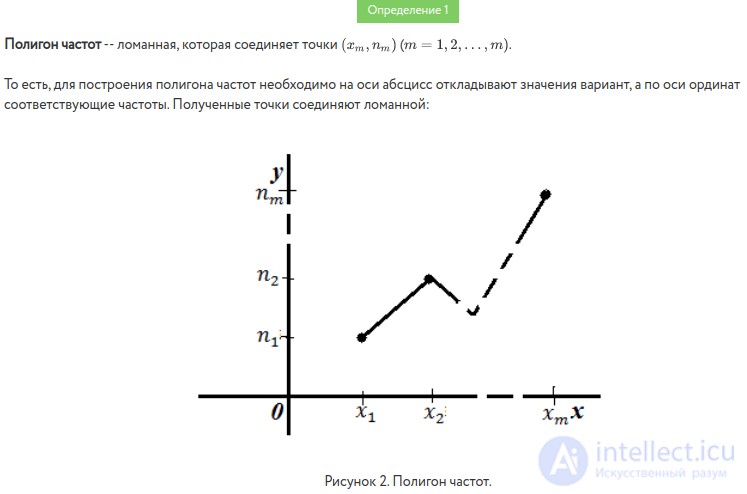
Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), ..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки ( xi; ni) соединяют отрезками прямых и получают полигон частот (Рис. 1).

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x1; W1), (x2; W2), ..., (xk; Wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им относительные частоты Wi. Точки ( xi; Wi) соединяют отрезками прямых и получают полигон относительных частот.

В случае непрерывного признака целесообразно строить гистограмму.

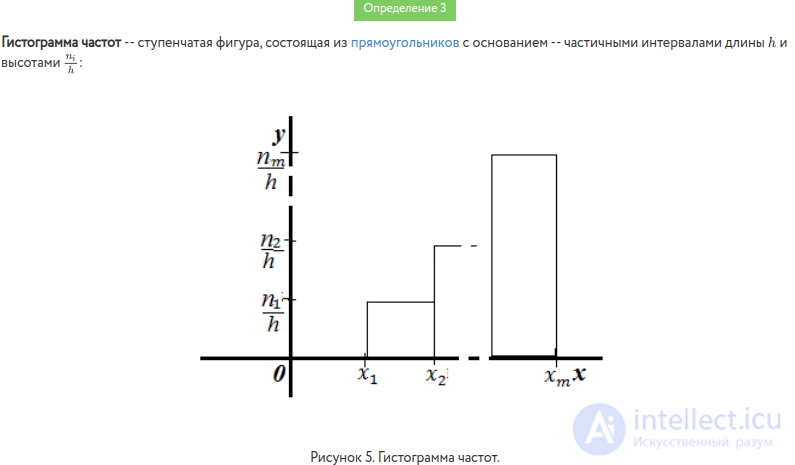
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению ni / h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni / h.

Площадь i - го частичного прямоугольника равна hni / h = ni - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

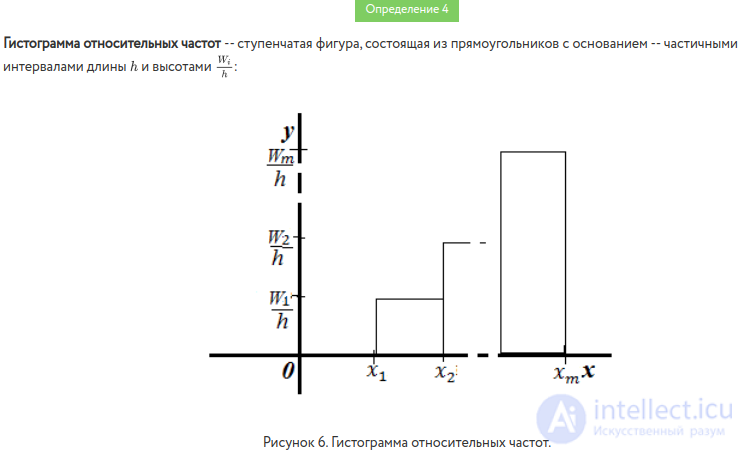
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi / h (Рис. Об этом говорит сайт https://intellect.icu . 2).

Площадь i - го частичного прямоугольника равна hWi / h = Wi - относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице.

Рис. 1. Полигон частот

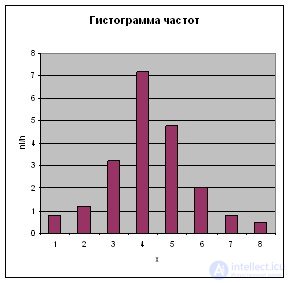
Рис. 2. Гистограмма относительных частот

пример построения гистограммы

Гистограмма дает наглядное графическое представление о распределении результатов измерений или каких лио днных.

Ее строят для интервальных рядов данных, причем число результатов должно быть достаточно большим (не менее 40).

Гистограмма явяется ступенчатой фигурой, состоящую из прямоугольников, основания которых равны границам интервалов, а высота соответствует абсолютным или относительным частотам попадания результатов в интервалы.

Для построения гистограммы выполняют следующее:

1. Расчет размаха R из n результатов измерений (размах – это разница между наибольшим Хmax и наименьшим Xmin значениями)

R= Xmax +Xmin . (1.11)

2. Определение количества интервалов k по формуле k = 1 + 3,3× lg n (1.12)

или по упрощенной формуле k = 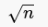(1.13)

Полученное значение k можно округлить. Обычно 6 < k < 20

3. Вычисление ширины интервалов гистограммы h, h = R/k . (3.14)

4. Расчет границ интервалов. Границы интервалов выбирают обычно таким образом, чтобы они не совпадали с результатами измерений и крайние интервалы были заполнены.

5. Подсчет числа попаданий результатов в интервалы. Полученные результаты сводят в таблицу.

6. Построение столбчатой гистограммы.

Если полученная гистограмма соответствует «колоколу» Гаусса (рис. 2.3), то результаты измерений распределены по нормальному закону и вероятно всего наблюдаются естественные природные процессы и величины. возможны и другие законов распределения

Пример. имееются 50 дневные измерения цен на голандский сыр в Долларах .

Необходимо определить закон распределения результатов измерения, построив гистограмму.

20,62	20,40	20,60	20,53	20,45	20,65	20,59	20,70	20,60	20,60
20,64	20,58	20,80	20,60	20,57	20,60	20,70	20,60	20,60	20,60
20,46	20,60	20,75	20,51	20,70	20,75	20,55	20,60	20,55	20,42
20,48	20,66	20,52	20,58	20,73	20,73	20,57	20,55	20,65	20,60
20,66	20,67	20,67	20,70	20,58	20,60	20,50	20,50	20,80	20,50

Решение.

Рассчитаем размах результатов R по формуле (3.11)

R = 20,80 – 20,40 = 0,40 доллар.

Определим количество интервалов по формуле (3.12):

k = 1 +3,3× lg 50 = 6,6 » 7.

По формуле (1.14) вычислим ширину интервалов

h = 0,4 / 7 = 0. 057 = 0,06 доллар

Далее составим таблицу, в которую запишем границы интервалов и частоту попадания результатов в указанные интервалы (табл. 1).

Наименьший результат измерения 20,40 доллар, поэтому нижнюю границу первого интервала целесообразно выбрать равной

20,40 - 0.06/2 = 20,37 доллар

Чтобы границы интервалов не совпадали с результатами, добавим к ним один разряд.

Таблица 1 Расчет гистограммы

Границы интервалов, доллар	Частота попадания в интервалы, hm	Относительная частота, hm/n
20,375 – 20,435	2	0,04
20,435 – 20,495	3	0,06
20,495 – 20,555	7	0,14
20,555 – 20,615	21	0,42
20,615 – 20,675	6	0,12
20,675 – 20,735	6	0,12
20,735 – 20,795	3	0,06
20,795 – 20,855	2	0,04
Итого	n = 50	Р = 1,00

Строим гистограмму. По оси абсцисс откладываем границы интервалов, а по оси ординат – абсолютные или относительные частоты (рис. 1.1).

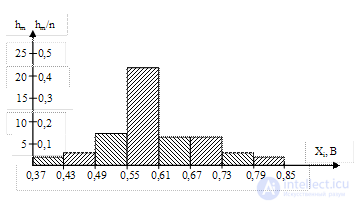
Рис.1.1. Гистограмма

построить гистограмму можно и редакторе EXCEL или Google Docs .

Полученная гистограмма соответствует «колоколу» Гаусса, что говорит о нормальном распределении результатов измерений напряжения

пример построения полигона частот

Спортивные достижения пловцов характеризуются данными, представленными в таблице.

Количество баллов x	1	2	3	4	5	6	7	8	9	10	11	12
Число спортсменов n	1	1	2	3	4	4	6	5	3	3	2	1

Построить полигон частот.

Решение.

Строим точки основываясь на данных из таблицы. Полученные точки соединяем отрезками прямой. Важно что точки (0; 0) и (13; 0), расположенные на оси абсцисс и имеющие своими абсциссами числа, на 1 меньшее и большее, чем соответственно абсциссы самой левой и самой правой точек.

Построим Полигон частот

Если полигон строят по данным интервального ряда, то в качестве абсцисс точек берут середины соответствующих интервалов.

Крайние левую и правую точки соединяют с точками оси абсцисс - серединами ближайших интервалов, частоты которых равны нулю.

Конечно, в этом случае полигон лишь приближенно отображает зависимость частот от значений аргумента.

Выводы

Вау!! 😲 Ты еще не читал? Это зря!

• выборочная функция распределения , эмпирическая функция распределения ,
• ряды распределения , полигон , гистограмма , кумулята ,
• Логнормальное распределение
• псевдокривая
• Статистический критерий

Надеюсь, эта статья про гистограмма, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое гистограмма, полигон, пример построения полигона, пример построения гистограммы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ