Лекция
Привет, Вы узнаете о том , что такое слепая подпись blind signature, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое слепая подпись blind signature , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Слепая подпись (Blind Signature) — разновидность ЭЦП, особенностью которой является то, что подписывающая сторона не может точно знать содержимое подписываемого документа. Понятие слепой подписи придумано Дэвидом Чаумом (англ.)[1] в 1982 году, им же предложена первая реализация через алгоритм RSA. Безопасность схемы слепой подписи основывалась на сложности факторизации больших составных чисел. С тех пор было предложено большое количество других схем[2][3].
Основная идея слепых подписей заключается в следующем:
По завершении этого протокола сторона В ничего не знает ни о сообщении t, ни о подписи под этим сообщением.
Эту схему можно сравнить с конвертом, в котором размещен документ и копировальный лист. Если подписать конверт, то подпись отпечатается на документе, и при вскрытии конверта документ уже будет подписан.
Цель слепой подписи состоит в том, чтобы воспрепятствовать подписывающему лицу В ознакомиться с сообщением стороны А, которое он подписывает, и с соответствующей подписью под этим сообщением. Поэтому в дальнейшем подписанное сообщение невозможно связать со стороной А.
Схема безопасной слепой подписи должна удовлетворять 3 свойствам, а именно :
1) Нулевое разглашение. Это свойство помогает пользователю получить подпись на данном сообщении, не раскрывая самого сообщения подписывающей стороне.
2) Непрослеживаемость. Подписывающая сторона не может отследить пару подпись-сообщение после того, как пользователь обнародовал подпись на своем сообщении.
3) Неподложность. Только подписывающая сторона может сгененировать действительную подпись. Это свойство самое важное и должно удовлетворяться для всех схем подписей.
Благодаря свойствам нулевого разглашения и непрослеживаемости, схема слепой подписи может быть широко задействована в приложениях, где необходима конфиденциальность, например, в системах электронного голосования[4] [5] [6] [7].
Дана ситуация: Боб — нотариус. Алисе нужно, чтобы он подписал документ, не имея никакого представления о его содержании. Боб только заверяет, что документ нотариально засвидетельствован в указанное время. Тогда они действуют по следующему алгоритму:
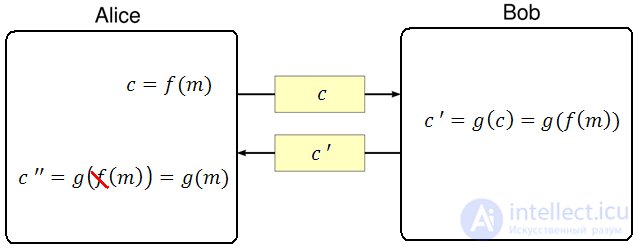
В этой схеме Алиса хочет, чтобы Боб вслепую подписал сообщение {\displaystyle m} . Для этого:
. Для этого:
 функцией {\displaystyle f}
функцией {\displaystyle f} , получая зашифрованное сообщение {\displaystyle c=f(m)}
, получая зашифрованное сообщение {\displaystyle c=f(m)} .
. функцией {\displaystyle g}
функцией {\displaystyle g} , получая {\displaystyle c^{'}=g(c)=g(f(m))}
, получая {\displaystyle c^{'}=g(c)=g(f(m))} .
. обратно Алисе.
обратно Алисе. и убирает свое шифрование, получая: {\displaystyle c^{''}=g(f(m))*f^{-1}=g(m)}
и убирает свое шифрование, получая: {\displaystyle c^{''}=g(f(m))*f^{-1}=g(m)} .
.Этот протокол работает, только если функции подписи и шифрования коммутативны.
Протокол RSA
Первая реализация слепых подписей была осуществлена Чаумом с помощью криптосистемы RSA:
Допустим, что изначально у Боба есть открытый ключ {\displaystyle (p,e)} , где {\displaystyle p}
, где {\displaystyle p} - это модуль, а {\displaystyle e}
- это модуль, а {\displaystyle e} - публичная экспонента ключа.
- публичная экспонента ключа.
 , взаимно простой с {\displaystyle p}
, взаимно простой с {\displaystyle p} , и вычисляет {\displaystyle m^{'}\equiv mr^{e}{\bmod {p}}}
, и вычисляет {\displaystyle m^{'}\equiv mr^{e}{\bmod {p}}} .
. по открытому каналу Бобу.
по открытому каналу Бобу. , используя свой закрытый ключ {\displaystyle (p,d)}
, используя свой закрытый ключ {\displaystyle (p,d)} .
. обратно Алисе.
обратно Алисе. следующим образом: {\displaystyle s\equiv s^{'}*r^{-1}{\bmod {p}}\equiv m^{d}{\bmod {p}}}
следующим образом: {\displaystyle s\equiv s^{'}*r^{-1}{\bmod {p}}\equiv m^{d}{\bmod {p}}} .
.Чаум придумал целое семейство более сложных алгоритмов слепой подписи под общим названием неожиданные слепые подписи. Об этом говорит сайт https://intellect.icu . Их схемы еще сложнее, но они дают больше возможностей[1].
Слепая подпись на основе ЭЦП Шнорра
Пусть Алиса хочет подписать сообщение {\displaystyle m} у Боба таким образом, чтобы, во-первых, Боб не мог ознакомиться с сообщением в ходе подписи, во-вторых, чтобы Боб не мог впоследствии при получении сообщения {\displaystyle m}
у Боба таким образом, чтобы, во-первых, Боб не мог ознакомиться с сообщением в ходе подписи, во-вторых, чтобы Боб не мог впоследствии при получении сообщения {\displaystyle m} и соответствующей подписи идентифицировать пользователя, инициировавшего протокол слепой подписи для данного конкретного сообщения (Алису). Данный протокол реализуется следующим образом:
и соответствующей подписи идентифицировать пользователя, инициировавшего протокол слепой подписи для данного конкретного сообщения (Алису). Данный протокол реализуется следующим образом:
 .
. (w и t - случайные числа, не превосходящие {\displaystyle y}
(w и t - случайные числа, не превосходящие {\displaystyle y} ), {\displaystyle E^{'}=H(m||R^{'})}
), {\displaystyle E^{'}=H(m||R^{'})} и {\displaystyle E=E^{'}+t\mod y}
и {\displaystyle E=E^{'}+t\mod y} , после чего отправляет Бобу значение{\displaystyle E}
, после чего отправляет Бобу значение{\displaystyle E} .
. , такое что {\displaystyle R=a^{S}y^{E}\mod p}
, такое что {\displaystyle R=a^{S}y^{E}\mod p} , и отправляет {\displaystyle S}
, и отправляет {\displaystyle S} Алисе.
Алисе. , где {\displaystyle E^{'}=E^{-t}\mod y}
, где {\displaystyle E^{'}=E^{-t}\mod y} и {\displaystyle S^{'}=S-w\mod y}
и {\displaystyle S^{'}=S-w\mod y} , которая является подлинной по отношению к сообщению {\displaystyle m}
, которая является подлинной по отношению к сообщению {\displaystyle m} [8].
[8].Доказательство
Подлинность подписи доказывается следующим образом. Из {\displaystyle R=a^{S}y^{E}\mod p} следует {\displaystyle Ra^{-w}y^{-t}=a^{S-w}y^{E-t}modp}
следует {\displaystyle Ra^{-w}y^{-t}=a^{S-w}y^{E-t}modp} и {\displaystyle R^{'}=a^{S^{'}}y^{E^{'}}\mod p}
и {\displaystyle R^{'}=a^{S^{'}}y^{E^{'}}\mod p} . При этом проблема анонимности решается, поскольку любая тройка {\displaystyle (R,S,E)}
. При этом проблема анонимности решается, поскольку любая тройка {\displaystyle (R,S,E)} из множества таких троек, которые формировались Бобом, может быть сопоставлена с подписью {\displaystyle (E^{'},S^{'})}
из множества таких троек, которые формировались Бобом, может быть сопоставлена с подписью {\displaystyle (E^{'},S^{'})} к данному документу {\displaystyle m}
к данному документу {\displaystyle m} . Действительно, имеем: {\displaystyle R=a^{S}y^{E}\mod p}
. Действительно, имеем: {\displaystyle R=a^{S}y^{E}\mod p} и {\displaystyle R^{'}=a^{S^{'}}y^{E^{'}}\mod p}
и {\displaystyle R^{'}=a^{S^{'}}y^{E^{'}}\mod p} {\displaystyle \Rightarrow }
{\displaystyle \Rightarrow } {\displaystyle R^{'}/R\equiv a^{S^{'}-S}y^{E^{'}-E}\mod p\equiv a^{-w}y^{-t}\mod p}
{\displaystyle R^{'}/R\equiv a^{S^{'}-S}y^{E^{'}-E}\mod p\equiv a^{-w}y^{-t}\mod p} , т.е. при равновероятном случайном выборе слагаемых {\displaystyle w}
, т.е. при равновероятном случайном выборе слагаемых {\displaystyle w} и {\displaystyle t}
и {\displaystyle t} подпись {\displaystyle (E^{'},S^{'})}
подпись {\displaystyle (E^{'},S^{'})} с равной вероятностью была порождена из любой тройки, входящей в множество троек, сформированных подписывающим. Отметим также, что Боб не имеет даже возможности доказать, что на момент формирования подписи данного документа {\displaystyle m}
с равной вероятностью была порождена из любой тройки, входящей в множество троек, сформированных подписывающим. Отметим также, что Боб не имеет даже возможности доказать, что на момент формирования подписи данного документа {\displaystyle m} он не был ознакомлен с ним.
он не был ознакомлен с ним.
Слепая подпись на основе ГОСТ Р 34.10-94
Параметры:
p — простое число, 510 ≤ |p| ≤ 512 (либо 1022 ≤ |p| ≤ 1024), где |p| — разрядность двоичного представления числа p.
q — большой простой делитель числа p-1, 255 ≤ |q| ≤ 256 (либо 511 ≤ |q| ≤ 512)
α ≠ 1, α < p, {\displaystyle \alpha ^{q}} mod p = 1.
mod p = 1.
Вычисление:
 mod p) mod q — первая часть подписи;
mod p) mod q — первая часть подписи;Проверка:
 mod p) mod q, где y — открытый ключ;
mod p) mod q, где y — открытый ключ;Слепая подпись на основе стандарта СТБ 1176.2-99
Стандарт Белоруссии предусматривает следующий протокол генерации слепой подписи к документу M:
 . Эти действия выполняет подписывающий. Далее он передает число R пользователю;
. Эти действия выполняет подписывающий. Далее он передает число R пользователю; , {\displaystyle E'=F_{H}(R'||M)}
, {\displaystyle E'=F_{H}(R'||M)} и E = E' - τ mod q; E — первый элемент подписи — направляется подписывающему;
и E = E' - τ mod q; E — первый элемент подписи — направляется подписывающему;В данном описании использованы следующие параметры: q — модуль, по которому ведутся вычисления, простое; a — порождающий элемент; x — закрытый ключ; y — открытый ключ[9].
Пусть {\displaystyle {\overline {y_{1},y_{s}}}} — открытые ключи, которыми владеют s пользователей. Пусть есть сообщение M, которое хотят подписать m из них. В таком случае все подписи можно объединить в одну, длина которой равна длине подписи одного пользователя и не зависит от m. Это реализуется по правилам следующего 1протокола:
— открытые ключи, которыми владеют s пользователей. Пусть есть сообщение M, которое хотят подписать m из них. В таком случае все подписи можно объединить в одну, длина которой равна длине подписи одного пользователя и не зависит от m. Это реализуется по правилам следующего 1протокола:
 < p, где j = {\displaystyle {\overline {1,m}}}
< p, где j = {\displaystyle {\overline {1,m}}} , p — большое простое число. Далее каждый из m пользователей вычисляет {\displaystyle R_{\alpha _{j}}=(t_{\alpha _{j}})^{k}}
, p — большое простое число. Далее каждый из m пользователей вычисляет {\displaystyle R_{\alpha _{j}}=(t_{\alpha _{j}})^{k}} mod p (k — большая простая степень) и рассылает это число всем остальным пользователям из данной группы.
mod p (k — большая простая степень) и рассылает это число всем остальным пользователям из данной группы. mod p. Далее вычисляется e = f(R,M) = RH mod q, где q — большое простое число, отличное от p, H = Hash(M) — хэш-функция. Число e будет первым элементом коллективной подписи.
mod p. Далее вычисляется e = f(R,M) = RH mod q, где q — большое простое число, отличное от p, H = Hash(M) — хэш-функция. Число e будет первым элементом коллективной подписи. mod p — доля пользователя. Эту долю каждый пользователь вычисляет и предоставляет остальным.
mod p — доля пользователя. Эту долю каждый пользователь вычисляет и предоставляет остальным. mod p. Это второй элемент коллективной подписи.
mod p. Это второй элемент коллективной подписи.Проверка коллективной слепой подписи
{\displaystyle y=\prod _{j=1}^{m}y_{\alpha _{j}}} mod p — коллективный открытый ключ. На его основе происходит проверка коллективной слепой подписи по следующему алгоритму:
mod p — коллективный открытый ключ. На его основе происходит проверка коллективной слепой подписи по следующему алгоритму:
 mod p.
mod p.Наиболее широкое применение протокол слепых подписей нашел в сфере цифровых денег. Например, чтобы вкладчик не обманул банк, может использоваться такой протокол: вкладчик пишет одинаковый номинал купюр на ста документах с разными номерами и депонирует в зашифрованном виде у банка. Банк выбирает случайным образом и требует раскрыть 99 (или n-1) конвертов, убеждается, что везде написано $10, а не $1000, тогда подписывает оставшийся конверт вслепую, не видя номера купюры.
Может быть предусмотрен более простой вариант: за каждым номиналом купюры у банка закреплена своя пара открытых ключей. Тогда под подпись присылается только номер купюры, и необходимость проверки номинала перед подписью отпадает[1].
Слепые подписи используются для тайного голосования. В протоколе Фуджиока, Окамото и Охта, избиратель подготавливает избирательный бюллетень со своим выбором, который он сделал, шифрует его секретным ключом, и маскирует его. Далее избиратель подписывает избирательный бюллетень и посылает его валидатору. Валидатор проверяет, что подпись принадлежит зарегистрированному избирателю, который еще не голосовал.
Если избирательный бюллетень действителен, валидатор подписывает избирательный бюллетень и возвращает его избирателю. Избиратель удаляет маскировку, раскрывая таким образом зашифрованный избирательный бюллетень, подписанный валидатором. Далее избиратель посылает в результате полученный подписанный, зашифрованный избирательный бюллетень счетчику, который проверяет подпись на зашифрованном избирательном бюллетене.
Если избирательный бюллетень действителен, счетчик размещает его в списке, который будет издан после всего голосования. После того, как список издан, избиратели проверяют, что их избирательные бюллетени находятся в списке и посылают счетчику ключи расшифрования, необходимые, чтобы открыть их избирательные бюллетени. Счетчик использует эти ключи для расшифрования избирательных бюллетеней и добавляет голос к общему числу. После выборов счетчик издает ключи расшифрования наряду с зашифрованными избирательными бюллетенями, чтобы избиратели могли независимо проверить выбор[10].
Алгоритм RSA может являться объектом атаки, благодаря которой становится возможным расшифровать ранее подписанное вслепую сообщение, выдав его за сообщение, которое только еще предстоит подписать. Исходя из того, что процесс подписи эквивалентен расшифровке подписывающей стороной (с использованием ее секретного ключа), атакующий может подложить для подписи уже подписанную вслепую версию сообщения {\displaystyle m} , зашифрованного с помощью открытого ключа подписывающей стороны, то есть подложить сообщение {\displaystyle m'}
, зашифрованного с помощью открытого ключа подписывающей стороны, то есть подложить сообщение {\displaystyle m'} .
.
{\displaystyle {\begin{aligned}m''&=m'r^{e}{\pmod {n}}\\&=(m^{e}{\pmod {n}}\cdot r^{e}){\pmod {n}}\\&=(mr)^{e}{\pmod {n}}\\\end{aligned}}}
где {\displaystyle m'} - это зашифрованная версия сообщения. Когда сообщение подписано, открытый текст {\displaystyle m}
- это зашифрованная версия сообщения. Когда сообщение подписано, открытый текст {\displaystyle m} легко извлекаем:
легко извлекаем:
{\displaystyle {\begin{aligned}s'&=m''^{d}{\pmod {n}}\\&=((mr)^{e}{\pmod {n}})^{d}{\pmod {n}}\\&=(mr)^{ed}{\pmod {n}}\\&=m\cdot r{\pmod {n}}{\mbox{, since }}ed\equiv 1{\pmod {\phi (n)}}\\\end{aligned}}}
где {\displaystyle \phi (n)} - это Функция Эйлера. Теперь сообщение легко получить.
- это Функция Эйлера. Теперь сообщение легко получить.
{\displaystyle {\begin{aligned}m=s'\cdot r^{-1}{\pmod {n}}\end{aligned}}}
Атака работает, потому что в этой схеме подписывающая сторона подписывает непосредственно само сообщение. Напротив, в обычных схемах подписи подписывающая сторона обычно подписывает, например, криптографическую хеш-функцию. Поэтому из-за этого мультипликативного свойства RSA, один ключ никогда не должен использоваться одновременно для шифрования и подписания вслепую[8].
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области слепая подпись blind signature имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое слепая подпись blind signature и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ