Лекция
Привет, сегодня поговорим про производящая функция последовательности, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое производящая функция последовательности, генератриса , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .
Производящая функция (или генератриса ) последовательности
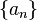— это формальный степенной ряд
.
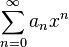Зачастую производящая функция последовательности чисел является рядом Тейлора некоторой аналитической функции, что может использоваться для изучения свойств самой последовательности. Однако, в общем случае производящая функция не обязана быть аналитической. Например, оба ряда
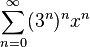и 
имеют радиус сходимости ноль, то есть расходятся во всех точках, кроме нуля, а в нуле оба равны 1, то есть как функции они совпадают; тем не менее, как формальные ряды они различаются.
Производящие функции дают возможность просто описывать многие сложные последовательности в комбинаторике, а иногда помогают найти для них явные формулы.
Метод производящих функций был разработан Эйлером в 1750-х годах.
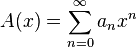и 
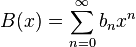последовательносте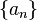й и 
является производящей функцией свертки 
этих последовательностей: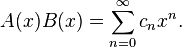
Пусть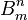 
— это количество композиций неотрицательного целого числа n длины m, то есть, представлений n в ви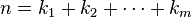де 
, где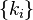 
— неотрицательные целые числа. Число 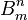также является числом сочетаний с повторениями из m по n, то есть, количество выборок n возможно повторяющих элементов из множества 
(при этом каждый член 
в композиции можно трактовать как количество элементов i в выборке).
При фиксированном m производящей функцией последовательности 
является:
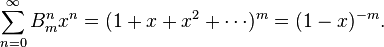
Поэтому число 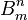может быть найдено как коэффициент при 
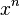в разложении 
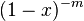по степеням x. Об этом говорит сайт https://intellect.icu . Для этого можно воспользоваться определениембиномиальных коэффициентов или же непосредственно взять n раз производную в нуле:
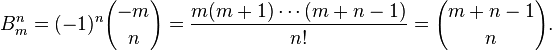
Генератриса чисел Белла має вигляд
.
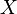— положительная целочисленная случайная величина (частный случай дискретной), имеющая распределение вероятностей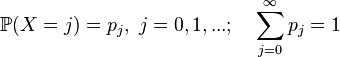
то ее математическое ожидание может быть выражено через производящую функцию последовательности 
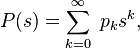
как значение первой производной в единице: 
(стоит отметить, что ряд для P(s) сходится, по крайней мере, при 
). Действительно,
При подстановке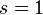 
получим величину 
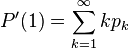, которая по определению является математическим ожиданием дискретной случайной величины. Если этот ряд расходится, то 
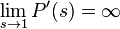-- а 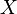имеет бесконечное математическое ожидание, 
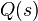последовательности «хвостов» распределения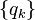 
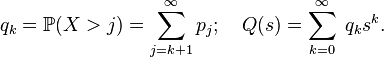
Эта производящая функция связана с определенной ранее функцией 
свойством: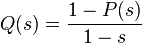 
при 
. Из этого по теореме о среднем следует, что математическое ожидание равно просто значению этой функции в единице:
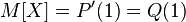
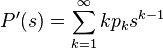и используя соотношение 
, получим:
Чтобы получить дисперсию 
, к этому выражению надо прибавить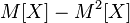 
, что приводит к следующим формулам для вычисления дисперсии:
.
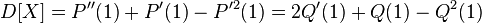В случае бесконечной дисперсии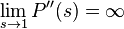 
.
Экспоненциальная производящая функция последовательности 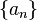— это формальный степенной ряд
.
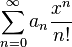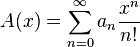и 
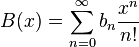— экспоненциальные производящие функции последовательностей 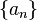и , то их произведение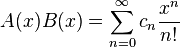 
является экспоненциальной производящей функцией последовательности 
.
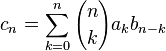Надеюсь, эта статья про производящая функция последовательности, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое производящая функция последовательности, генератриса и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ
Из статьи мы узнали кратко, но содержательно про производящая функция последовательности
Комментарии
Оставить комментарий
Теория вероятностей. Математическая статистика и Стохастический анализ
Термины: Теория вероятностей. Математическая статистика и Стохастический анализ