16.1.Метод канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций кратко

Привет, Вы узнаете о том , что такое метод канонических разложений, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое метод канонических разложений, представление случайной функции в виде суммы элементарных случайных функций , настоятельно рекомендую прочитать все из категории Теория вероятностей. Математическая статистика и Стохастический анализ .

В 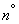15.7 мы познакомились с общими правилами линейных преобразований случайных функций. Эти правила сводятся к тому, что при линейном преобразовании случайной функции ее математическое ожидание подвергается тому же линейному преобразованию, а корреляционная функция подвергается этому преобразованию дважды: по одному и другому аргументу.

Правило преобразования математического ожидания очень просто и при практическом применении затруднений не вызывает. Что касается двойного преобразования корреляционной функции, то оно в ряде случаев приводит к чрезвычайно сложным и громоздким операциям, что затрудняет практическое применение изложенных общих методов.

Действительно, рассмотрим, например, простейший интегральный оператор:

. (16.1.1)

Согласно общему правилу корреляционная функция преобразуется тем же оператором дважды:

. (16.1.2)

Очень часто бывает, что полученная из опыта корреляционная функция 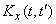не имеет аналитического выражения и задана таблично; тогда интеграл (16.1.2) приходится вычислять численно, определяя его как функцию обоих пределов. Это - задача очень громоздкая и трудоемкая. Если даже аппроксимировать подынтегральную функцию каким-либо аналитическим выражением, то и в этом случае чаще всего интеграл (16.1.2) через известные функции не выражается. Так обстоит дело даже при простейшей форме оператора преобразования. Если же, как часто бывает, работа динамической системы описывается дифференциальными уравнениями, решение которых не выражается в явной форме, задача об определении корреляционной функции на выходе еще более осложняется: она требует интегрирования дифференциальных уравнений с частными производными.

В связи с этим на практике применение изложенных общих методов линейных преобразований случайных функций, как правило, оказывается слишком сложным и себя не оправдывает. При решении практических задач значительно чаще применяются другие методы, приводящие к более простым преобразованиям. Один из них - так называемый метод канонических разложений , разработанный В. С. Пугачевым, и составляет содержание данной главы.

Идея метода канонических разложений состоит в том, что случайная функция, над которой нужно произвести те или иные преобразования, предварительно представляется в виде суммы так называемых элементарных случайных функций.

Элементарной случайной функцией называется функция вида:

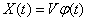, (16.1.3)

где 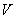- обычная случайная величина, 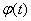- обычная (неслучайная) функция.

Элементарная случайная функция является наиболее простым типом случайной функции. Действительно, в выражении (16.1.3) случайным является только множитель 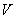, стоящий перед функцией 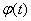; сама же зависимость от времени случайной не является.

Все возможные реализации элементарной случайной функции 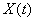могут быть получены из графика функции простым измерением масштаба по оси ординат (рис. 16.1.1).

Рис. 16.1.1.

При этом ось абсцисс 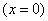также представляет собой одну из возможных реализаций случайной функции 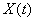, осуществляющуюся, когда случайная величина 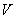принимает значение 0 (если это значение принадлежит к числу возможных значений величины ).

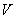В качестве примеров элементарных случайных функций приведем функции (рис. Об этом говорит сайт https://intellect.icu . 16.1.2) и 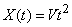(рис. 16.1.3).

Рис. 16.1.2.

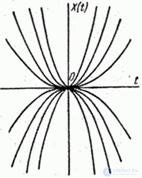
Рис. 16.1.3.

Элементарная случайная функция характерна тем, что в ней разделены две особенности случайной функции: случайность вся сосредоточена в коэффициенте 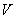, а зависимость от времени - в обычной функции .

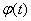Определим характеристики элементарной случайной функции (16.1.3). Имеем:

,

где - математическое ожидание случайной величины .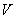

Если , математическое ожидание случайной функции 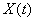также равно нулю, причем тождественно:

.

Мы знаем, что любую случайную функцию можно центрировать, т. е. привести к такому виду, когда ее математическое ожидание равно нулю. Поэтому в дальнейшем мы будем рассматривать только центрированные элементарные случайные функции для которых ; ; .

Определим корреляционную функцию элементарной случайной функции 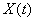. Имеем:

,

где - дисперсия величины .

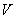Над элементарными случайными функциями весьма просто выполняются всевозможные линейные преобразования.

Например, продифференцируем случайную функцию (16.1.3). Случайная величина 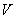, не зависящая от 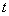, выйдет за знак производной, и мы получим:

.

Аналогично

.

Вообще, если элементарная случайная функция (16.1.3) преобразуется линейным оператором 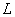, то при этом случайный множитель 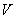, как не зависящий от 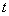, выходит за знак оператора, а неслучайная функция 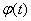преобразуется тем же оператором :

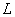. (16.1.4)

Значит, если элементарная случайная функция поступает на вход линейной системы, то задача ее преобразования сводится к простой задаче преобразования одной неслучайной функции 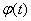. Отсюда возникает идея: если на вход динамической системы поступает некоторая случайная функция общего вида, то можно ее представить - точно или приближенно - в виде суммы элементарных случайных функций и только затем подвергать преобразованию. Такая идея разложения случайной функции на сумму элементарных случайных функций и лежит в основе метода канонических разложений.

Пусть имеется случайная функция:

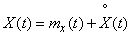. (16.1.5)

Допустим, что нам удалось - точно или приближенно - представить ее в виде суммы

, (16.1.6)

где - случайные величины с математическими ожиданиями, равными нулю; - неслучайные функции; 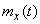- математическое ожидание функции .

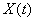Условимся называть представление случайной функции в форме (16.1.6) разложением случайной функции. Случайные величины будем называть коэффициентами разложения, а неслучайные функции - координатными функциями.

Определим реакцию линейной системы с оператором 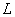на случайную функцию 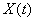, заданную в виде разложения (16.1.6). Известно, что линейная система обладает так называемым свойством суперпозиции, состоящим в том, что реакция системы на сумму нескольких воздействий равна сумме реакций системы на каждое отдельное воздействие. Действительно, оператор системы 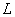, будучи линейным, может, по определению, применяться к сумме почленно.

Обозначая реакцию системы на случайное воздействие 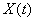, имеем:

. (16.1.7)

Придадим выражению (16.1.7) несколько иную форму. Учитывая общее правило линейного преобразования математического ожидания, убеждаемся, что

.

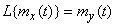Обозначая

,

имеем:

. (16.1.8)

Выражение (16.1.8) представляет собой не что иное, как разложение случайной функции по элементарным функциям. Коэффициентами этого разложения являются те же случайные величины , а математическое ожидание и координатные функции получены из математического ожидания и координатных функций исходной случайной функции тем же линейным преобразованием 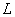, какому подвергается случайная функция .

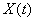Резюмируя, получаем следующее правило преобразования случайной функции, заданной разложением.

Если случайная функция 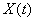, заданная разложением по элементарным функциям, подвергается линейному преобразованию , то коэффициенты разложения остаются неизменными, а математическое ожидание и координатные функции подвергаются тому же линейному преобразованию .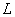

Таким образом, смысл представления случайной функции в виде разложения сводится к тому, чтобы свести линейное преобразование случайной функции к таким же линейным преобразованиям нескольких неслучайных функций - математического ожидания и координатных функций. Это позволяет значительно упростить решение задачи нахождения характеристик случайной функции по сравнению с общим решением, данным в 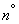15.7. Действительно, каждая из неслучайных 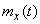функций , в данном случае преобразуется только один раз в отличие от корреляционной функции 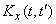, которая, согласно общим правилам, преобразуется дважды.

Информация, изложенная в данной статье про метод канонических разложений , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое метод канонических разложений, представление случайной функции в виде суммы элементарных случайных функций и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория вероятностей. Математическая статистика и Стохастический анализ

Из статьи мы узнали кратко, но содержательно про метод канонических разложений