Лекция
Привет, сегодня поговорим про факториал, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое факториал, суперфакториал, гиперфакториал, примориал , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
факториал числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральныхчисел от 1 до n включительно:

Например:
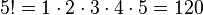 .
.
По договоренности:  . Также это равенство выполняется естественным образом:
. Также это равенство выполняется естественным образом:
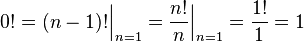
Факториал определен только для целых неотрицательных чисел.
Последовательность факториалов неотрицательных целых чисел начинается так:

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.
Факториал является чрезвычайно быстро растущей функцией. Он растет быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция  ).
).
В математике существует около десятка различных факториалов, рассмотрим их
пример 5! = 1*2*3*4*5
Возникает естественным образом в комбинаторике - науке, в которой изучаются задачи, связанные с выбором и расположением различных элементов чаще всего конечных множеств.
пример 7!! = 7*5*3*1
общий случай n!!= если n четное , то = n(n-2) * ... * 4 * 2 или
если n - не четное , то = n(n-2) * ... * 3 * 1
Этот факториал имеет просто громадное количество приложений в комбинаторике и достоин отдельного материала. Впервые он использовался при выводе замечательного произведения Уоллиса, связывающего натуральные числа и число π:

Этот представитель семейства в отличие от обычного факториала, который определяет количество перестановок, определяет количество беспорядков.

Определяется как произведение простых чисел, меньших или равных данному.

Название дано создателем уникальной в своем роде Онлайн Энциклопедии Целочисленных Последовательностей (OEIS). Определяется как произведение факториалов чисел, меньших или равных заданному.
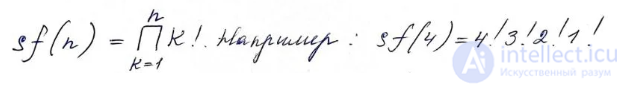

удивительно быстрорастущая функция. Для числа 3 - это уже вот такая невообразимая башня:
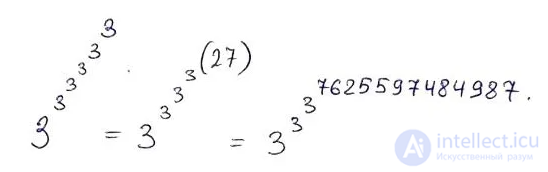
По сравнению с предыдущим представителем растет "медленно". Об этом говорит сайт https://intellect.icu . Например, для выражения выше - это 262144. Конечно, для числа 6 в результате уже  нулей.
нулей.
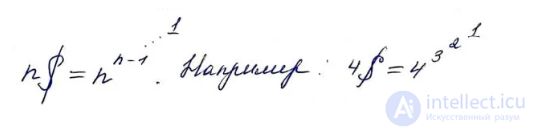
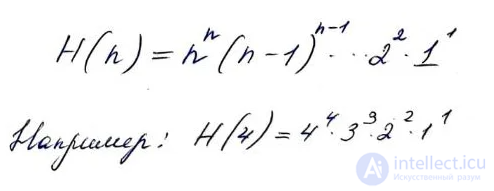
Растет еще медленнее, чем предшествующие два. Только лишь на 14 шаге число нулей приближается к гуголу.
Равняется произведению первых n чисел Фибоначчи.
А также факториал дробного числа.
Факториал дробного числа - факториал вычисляемый от аргумента -
Вычисляется по формуле:
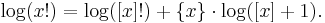
где [x] — целая часть чиcла x, {x} — дробная часть числа x.
Например, для x=11,2 будем иметь log(11,2!) = log(11!) + 0,2*log(12)
Вычисляемое таким способом значение факториала дробного числа является приближенным. Для точных расчетов необходимо использовать гамма-функцию.
Факториалы нецелых (дробных) чисел появляются при статистическом описании нейросетевых преобразователей биометрия/код ключа доступа биномиальным законом распределения зависмимых биометрических данных.
Факториалы использовались для подсчета перестановок, по крайней мере, еще в 12 веке индийскими учеными. В 1677 году Фабиан Стедман описал факториалы применительно к смене звонков (сигналов вызова) , музыкальному искусству, включающему звон многих настроенных колоколов. После описания рекурсивного подхода Стедман дает утверждение факториала (используя язык оригинала):
Теперь природа этих методов такова, что изменения на одном числе охватывают [включают] изменения на всех меньших числах ... настолько, что полный Пил(звон) изменений на одном числе, по-видимому, формируется путем объединения завершенных Пилсов(серии звонков) на всех меньшие числа в одно целое тело.
Обозначения п ! был введен французским математиком Кристианом Крампом в 1808 году.
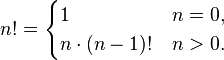
В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:
Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом.
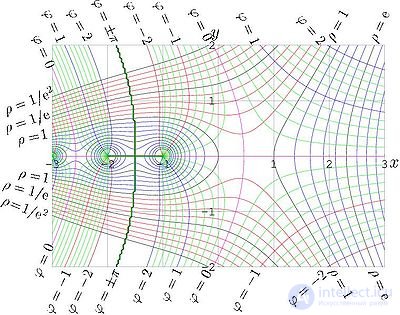
Амплитуда и фаза факториала комплексного аргумента.
Факториал связан с гамма-функцией от целочисленного аргумента соотношением:
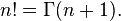
Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.
Путем аналитического продолжения ее также расширяют и на всю комплексную плоскость, исключаяособые точки при 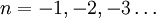 .
.
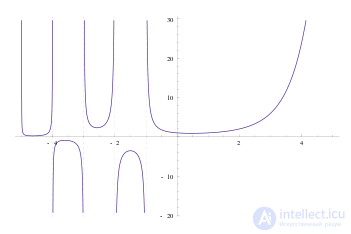
Пи-функция, определенная для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как
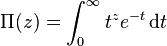 .
.
Поскольку 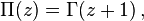 то пи-функция натурального числа совпадает с его факториалом:
то пи-функция натурального числа совпадает с его факториалом: 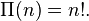 Как факториал, пи-функция удовлетворяет рекурсивному соотношению
Как факториал, пи-функция удовлетворяет рекурсивному соотношению 
Формула Стирлинга
Формула Стирлинга — асимптотическая формула для вычисления факториала:
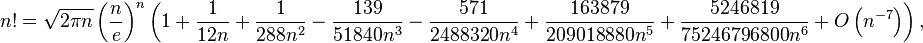
см. O-большое .
Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:
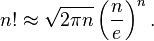
При этом можно утверждать, что
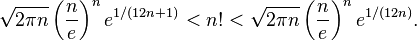
Формула Стирлинга позволяет получить приближенные значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что
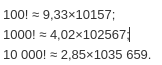
Каждое простое число p входит в разложение n! на простые множители в степени
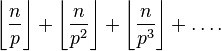
Таким образом,
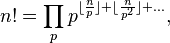
где произведение берется по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.
Для целого неотрицательного числа n:
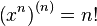
Например:
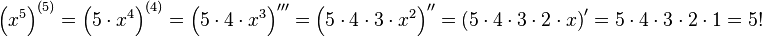
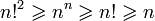
Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же четность, что и n.
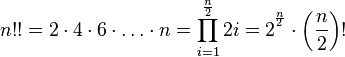
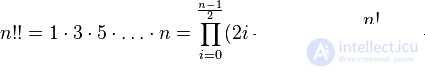
Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.
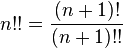
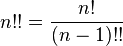
Выведение формул
Осуществив замену  для четного n и
для четного n и 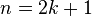 для нечетного n соответственно, где
для нечетного n соответственно, где 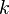 — целое неотрицательное число, получим:
— целое неотрицательное число, получим:
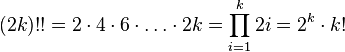

По договоренности: 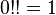 . Также это равенство выполняется естественным образом:
. Также это равенство выполняется естественным образом:

Двойной факториал, также как и обычный факториал, определен только для целых неотрицательных чисел.
Последовательность значений n!! начинается так:
1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, … .
m-кратный факториал числа n обозначается 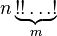 и определяется следующим образом. Пусть число n представимо в виде
и определяется следующим образом. Пусть число n представимо в виде 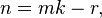 где
где 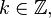
 Тогда
Тогда

Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно.
Кратный факториал связан с гамма-функцией следующим соотношением :
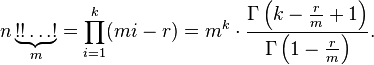
Убывающий факториал
Убывающим факториалом называется выражение
![(n)_k = n^{\underline{k}} = n^{[k]}= n\cdot (n-1)\cdot \ldots\cdot (n-k+1) = \frac{n!}{(n-k)!} = \prod_{i=n-k+1}^n i](/th/25/blogs/id4266/39_ba4964a955a39770c64cdb7bbd6ce5f4.png) .
.
Например:
n = 7; k = 4,
(n − k) + 1 = 4,
3k = 7 • 6 • 5 • 4 = 840.
Убывающий факториал дает число размещений из n по k.
Возрастающий факториал
Возрастающим факториалом называется выражение

Сюда перенаправляется запрос «Праймориал». На эту тему нужна отдельная статья.
Праймориал или примориал (англ. primorial) числа n обозначается pn# и определяется как произведение n первых простых чисел. Например,
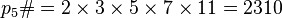 .
.
Иногда праймориалом называют число 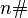 , определяемое как произведение всех простых чисел, не превышающих заданное n.
, определяемое как произведение всех простых чисел, не превышающих заданное n.
Последовательность праймориалов (включая 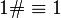 ) начинается так:
) начинается так:
1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, … .
Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырех равен
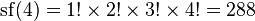
(поскольку устоявшегося обозначения нет, используется функциональное).
В общем
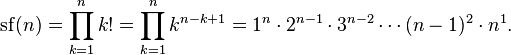
Последовательность суперфакториалов чисел  начинается так: 1, 1, 2, 12, 288, 34 560, 24 883 200, … .
начинается так: 1, 1, 2, 12, 288, 34 560, 24 883 200, … .
Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых nсуперфакториалов. Последовательность гиперфакториалов чисел  начинается так:
начинается так:
1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207 999 802 072 984 424 331 678 589 933 649 915 805 696 000 000 000 000 000 … .
Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение первых n (m−1)-уровневых факториалов, то есть
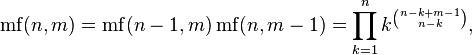
где 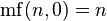 для
для  и
и 
Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.
Субфакториал числа n (обозначение: !n) определяется как количество беспорядков порядка n, то есть перестановок порядка n без неподвижных точек. Название субфакториал происходит из аналогии с факториалом, определяющим общее количество перестановок.
В частности, !n есть число способов положить n писем в n конвертов (по одному в каждый), чтобы ни одно не попало в соответствующий конверт (так называемая Задача о письмах).
«Примеры реализации функции факториал»
Список факторионов
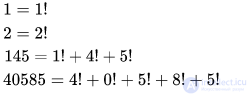
На этом все! Теперь вы знаете все про факториал, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое факториал, суперфакториал, гиперфакториал, примориал и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.