Лекция
Сразу хочу сказать, что здесь никакой воды про алгебра высказываний, и только нужная информация. Для того чтобы лучше понимать что такое алгебра высказываний , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
алгебра высказываний является составной частью одного из современных быстро развивающихся разделов математики – математической логики. Математическая логика применяется в информатике, позволяет моделировать простейшие мыслительные процессы. Одним из занимательных приложений алгебры высказываний – решение логических задач.
Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями . Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика, в отличие от, например, троичной логики.
Своим существованием наука «алгебра логики» обязана английскому математику Джорджу Булю, который исследовал логику высказываний. Первый в России курс по алгебре логики был прочитан П. С. Порецким в Казанском государственном университете.
Основоположником ее является Дж. Буль, английский математик и логик, положивший в основу своего логического учения аналогию между алгеброй и логикой. Алгебра логики стала первой системой математической логики, в которой алгебраическая символика стала применяться к логическим выводам в операциях с понятиями, рассматриваемыми со стороны их объемов. Буль ставил перед собой задачу решить логические задачи с помощью методов, применяемых в алгебре. Любое суждение он пытался выразить в виде уравнений с символами, в которых действуют логические законы, подобные законам алгебры.
Впоследствии усовершенствованием алгебры логики занимались У. С. Джевонс, Э. Шредер, П. С. Порецкий, Ч. Пирс, Г. Фреге, разработавший теорию исчисления высказываний, Д. Гильберт, добившийся успехов в области применения метода формализации в операциях с логическими высказываниями. Внесли свой вклад Б. Рассел, придавший вместе с А. Уайтхедом, математической логике современный вид; И. И. Жегалкин, заслугой которого явилась дальнейшая разработка исчисления классов и значительное упрощение теории операций логического сложения; В. И. Гливенко вынес предмет алгебры логики далеко за рамки изучения объемных операций с понятиями.
Алгебра логики в ее современном изложении занимается исследованием операций с высказываниями, то есть с предложениями, которые характеризуются только одним качеством — истинностным значением (истина, ложь). В классической алгебре логики высказывание одновременно может иметь только одно из двух истинностных значений: «истина» или «ложь». Алгебра логики исследует также высказывания — функции, которые могут принимать значения «истина» и «ложь» в зависимости от того какое значение будет придано переменной, входящей в высказывание — функцию.
Алгебра – это наука, которая изучает множество некоторых элементов и действия (операции) над ними. Если элементы алгебры – натуральные числа, а операции – сложение и умножение, то это алгебра натуральных чисел. Действия с направленными отрезками (векторами) изучает векторная алгебра.
Объектами алгебры высказываний являются высказывания. Высказывание – это истинное или ложное повествовательное предложение. Повествовательное предложение, в котором говорится об одном-единственном событии, называется простым высказыванием. Например, предложение «Луна – спутник Земли» есть простое высказывание, предложение «Не сорить!» не является высказыванием.
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.
Высказывания строятся над множеством {B, 
, 
, 
, 0, 1}, где B — непустое множество, над элементами которого определены три операции:
отрицание (унарная операция),
конъюнкция (бинарная),
дизъюнкция (бинарная),
а логический ноль 0 и логическая единица 1 — константы.
Так же используются названия
).
).Унарная операция отрицания в тексте формул оформляется либо в виде значка перед операндом (
) либо в виде черты над операндом (
), что компактнее, но в целом менее заметно.
Высказывания обозначаются большими буквами латинского алфавита. Если высказывание A истинно, то пишут A = 1, если ложно, то используют запись A = 0.
Как и в других алгебрах, в алгебре высказываний над ее объектами (высказываниями) определены действия, выполняя которые получают новые высказывания. Объединение двух высказываний в одно при помощи союза «И» называется операцией логического умножения. Полученное таким образом высказывание называется логическим произведением. Например, высказывание A – «В лесу растут грибы», высказывание B – «Льюис Кэрролл – математик», составим произведение этих высказываний AB – «В лесу растут грибы и Льюис Кэрролл – математик». Истинность произведения высказываний зависит от истинности перемножаемых высказываний и может быть определена с помощью следующей таблицы:
| А | В | АВ |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Объединение двух высказываний в одно с помощью союза «ИЛИ», употребляемого в неисключающем смысле, называется операцией логического сложения. Например, высказывание A – «Декабрь – зимний месяц», В – «Летом иногда идет дождь», определим высказывание A+B – «Декабрь – зимний месяц или летом иногда идет дождь». Установить истинность логической суммы можно с помощью следующей таблицы:
| А | В | А+В |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Операция логического отрицания осуществляется над одним высказыванием. Об этом говорит сайт https://intellect.icu . Выполнить операцию логического отрицания (обозначается 
) – значит получить из данного высказывания новое, присоединяя слова «неверно, что …» ко всему высказыванию. Истинность высказывания 
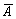определяется таблицей:
| А |  |
| 1 | 0 |
| 0 | 1 |
Пользуясь определенными выше операциями, можно из простых высказываний образовывать сложные. Например, всевозможные значения для высказывания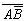 
можно записать в виде таблицы
| А | B |  |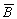
A |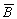
|
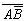| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
, инволютивность отрицания, закон снятия двойного отрицания
Среди высказываний особое место занимают те, в таблице истинности которых либо одни единицы, либо только нули. Это означает, что высказывание либо всегда истинно, либо ложно, независимо от истинности входящих в него высказываний. Например, высказывание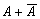 
всегда истинно, а высказывание 
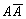всегда ложно. Доказать это можно составив таблицу истинности этих высказываний.
Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными.
Тождественно истинные или тождественно ложные высказывания, если они встречаются в формулах, заменяются в них, соответственно единицей или нулем:
, 
.
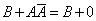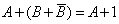Среди высказываний встречаются такие, таблицы истинности которых совпадают. Эти высказывания называются эквивалентными. Эквивалентными являются, например, высказывания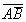 
и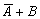 
(то есть 
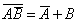). Это можно проверить составив таблицы истинности этих высказываний:
|
A |
B |
|
 |
 |
|
|
|
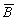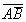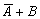1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
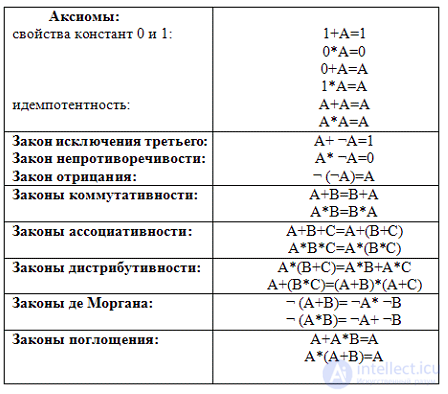
Операции алгебры высказываний обладают следующими важными свойствами:
| Логическое умножение: | Логическое сложение: |
| A·B = B·A | A + B = B + A |
| (AB)C = A(BC) | (A + B)+ C = A + (B + C) |
| A·A = A | A + A = A |
| A·1 = A | A + 1 = 1 |
| A·0 = 0 | A + 0 = A |
| A(B + C) = AB + AC | A + BC = (A + B)(A + C)A + BC = (A + B)(A + C) |
 |
 |
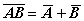Отрицание:
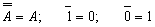
Формулы, выделенные жирным шрифтом, называются формулами Августа де Моргана (1806–1871). Используя эти формулы, можно, в частности, преобразовывать высказывания: сложные заменять более простыми.
В алгебре высказываний, как и в другой алгебре, возможны тождественные преобразования, но логическое сложение и умножение обладают специфическими свойствами A + A = A, AA = A, A + 1 = A. Это приводит к необычности действий над многочленами алгебры высказываний. Пусть нужно перемножить два сложных высказывания:
(A + B)(A + C) = AA + AC + AB + BC = A + AB + AC + BC.
Рассмотрим теперь два первых слагаемых A + AB = A(1 + B) = A1 = A и аналогично A+ AC = A. Таким образом, окончательно получаем (A + B)(A + C) = A+ BC.
Преобразование A + AB = A очень часто встречается в алгебре высказываний и называется «поглощение». Есть еще один вид столь же часто встречающегося тождественного преобразования, которое называется «склеивание».
Суть его состоит в следующем: 
(склеивание произошло по символу B). Соответственно для сложного высказывания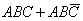 
склейку можно произвести по символу 
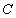, то есть имеет место тождественное преобразование 
.
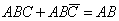Рассмотренных выше законы алгебры высказываний могут быть применены к решению логических задач Например:
Задача:
Алеша, Боря и Гриша откопали древний сосуд. О том, где и когда он был изготовлен, каждый из школьников высказал по два предположения:
Алеша: «Это сосуд греческий и сосуд изготовлен в V веке»;
Боря: «Это сосуд финикийский и сосуд изготовлен в III веке»;
Гриша: «Это не греческий сосуд и изготовлен он в IV веке».
Учитель истории сказал ребятам, что каждый из них прав только в одном их двух своих предположений. Где и в каком веке изготовлен сосуд?
Решение:
Введем обозначения простых высказываний:
«Это сосуд греческий» –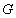 
;
«Это сосуд финикийский» – F;
«Сосуд изготовлен в V веке» – 5;
«Сосуд изготовлен в III веке» – 3;
«Сосуд изготовлен в IV веке» – 4.
Можно составить формулы высказываний каждого из школьников с учетом высказывания учителя. Формула Алешиного высказывания имеет вид G5. Учитель сказал, что Алеша прав только в одном из своих утверждений, поэтому либо G = 1, либо 5 = 1. Истинным будет высказывание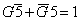 
, то есть высказывание «Сосуд греческий и изготовлен не в 5 веке или сосуд не греческий и изготовлен в 5 веке». Аналогично, высказывание Бори можно представить формулой 
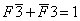и высказывание Гриши формулой 
.
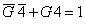Полученные формулы можно рассматривать как логические уравнения и решать систему:
.
Первое высказывание умножается на второе:
.
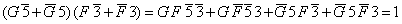Произведение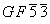 
– ложно потому, что сосуд не может быть изготовлен одновременно в Греции и Финикии, произведение 
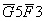– ложно потому, что сосуд не может быть изготовлен одновременно в 3 и 5 вв. После исключения этих высказываний получается следующее уравнение: 
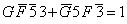. Это уравнение умножается на третье логическое уравнение составленной системы:
.
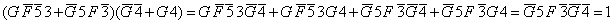Высказывания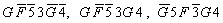 
исключены как ложные. Из полученного высказывания 
следует, что «Сосуд изготовлен в Финикии и сосуд изготовлен в 5 веке». Это утверждение согласуется с данными поставленной задачи.
На примере решения логической задачи продемонстрирована смысловая взаимосвязь входящих в сложное высказывание простых высказываний. В состав сложных высказываний могут входить взаимосвязанные по смыслу высказывания, однако Высказывания могут быть и противоречивыми. Таким образом, одним из применений алгебры высказываний является использование ее для анализа сложных, а подчас противоречивых текстов. Алгебра высказываний позволяет научиться моделировать простейшие мыслительные процессы. «Методы эти позволяют Вам обрести ясность мысли, способность находить собственное оригинальное решение трудных задач, вырабатывают у Вас привычку к систематическому мышлению и, что особенно ценно, умение обнаруживать логические ошибки, изъяны и пробелы тех, кто не пытался овладеть привлекательным искусством логики. Попытайтесь. Вот все, о чем я прошу вас», – Льюис Кэрролл (псевдоним Чарльза Лютвиджа Доджсона (1832–1898)) – известный английский математик и литератор.
А как ты думаешь, при улучшении алгебра высказываний, будет лучше нам? Надеюсь, что теперь ты понял что такое алгебра высказываний и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.